2025
JEE Advanced 2025 Paper 2 OnlineJEE Advanced 2025 Paper 1 Online2024
JEE Advanced 2024 Paper 2 OnlineJEE Advanced 2024 Paper 1 Online2023
JEE Advanced 2023 Paper 2 OnlineJEE Advanced 2023 Paper 1 Online2022
JEE Advanced 2022 Paper 2 OnlineJEE Advanced 2022 Paper 1 Online2021
JEE Advanced 2021 Paper 2 OnlineJEE Advanced 2021 Paper 1 Online2020
JEE Advanced 2020 Paper 2 OfflineJEE Advanced 2020 Paper 1 Offline2019
JEE Advanced 2019 Paper 2 OfflineJEE Advanced 2019 Paper 1 Offline2018
JEE Advanced 2018 Paper 2 OfflineJEE Advanced 2018 Paper 1 Offline2017
JEE Advanced 2017 Paper 2 OfflineJEE Advanced 2017 Paper 1 Offline2016
JEE Advanced 2016 Paper 2 OfflineJEE Advanced 2016 Paper 1 Offline2015
JEE Advanced 2015 Paper 2 OfflineJEE Advanced 2015 Paper 1 Offline2014
JEE Advanced 2014 Paper 2 OfflineJEE Advanced 2014 Paper 1 Offline2013
JEE Advanced 2013 Paper 2 OfflineJEE Advanced 2013 Paper 1 Offline2012
IIT-JEE 2012 Paper 2 OfflineIIT-JEE 2012 Paper 1 Offline2011
IIT-JEE 2011 Paper 1 OfflineIIT-JEE 2011 Paper 2 Offline2010
IIT-JEE 2010 Paper 2 OfflineIIT-JEE 2010 Paper 1 Offline2009
IIT-JEE 2009 Paper 2 OfflineIIT-JEE 2009 Paper 1 Offline2008
IIT-JEE 2008 Paper 2 OfflineIIT-JEE 2008 Paper 1 Offline2007
IIT-JEE 2007IIT-JEE 2007 Paper 2 Offline2006
IIT-JEE 2006IIT-JEE 2006 Screening2005
IIT-JEE 2005 ScreeningIIT-JEE 20052004
IIT-JEE 2004IIT-JEE 2004 Screening2003
IIT-JEE 2003IIT-JEE 2003 Screening2002
IIT-JEE 2002IIT-JEE 2002 Screening2001
IIT-JEE 2001IIT-JEE 2001 Screening2000
IIT-JEE 2000 ScreeningIIT-JEE 20001999
IIT-JEE 1999 ScreeningIIT-JEE 19991998
IIT-JEE 1998IIT-JEE 1998 Screening1997
IIT-JEE 19971996
IIT-JEE 19961995
IIT-JEE 1995 ScreeningIIT-JEE 19951994
IIT-JEE 19941993
IIT-JEE 19931992
IIT-JEE 19921991
IIT-JEE 19911990
IIT-JEE 19901989
IIT-JEE 19891988
IIT-JEE 19881987
IIT-JEE 19871986
IIT-JEE 19861985
IIT-JEE 19851984
IIT-JEE 19841983
IIT-JEE 19831982
IIT-JEE 19821981
IIT-JEE 19811980
IIT-JEE 19801979
IIT-JEE 19791978
IIT-JEE 1978JEE Advanced 2017 Paper 1 Offline
Paper was held on Sat, May 20, 2017 9:00 PM
Chemistry
1
An ideal gas is expanded from $$\left( {{p_1},{V_1},{T_1}} \right)$$ to $$\left( {{p_2},{V_2},{T_2}} \right)$$ under different conditions. The correct statement(s) among the following is (are)
2
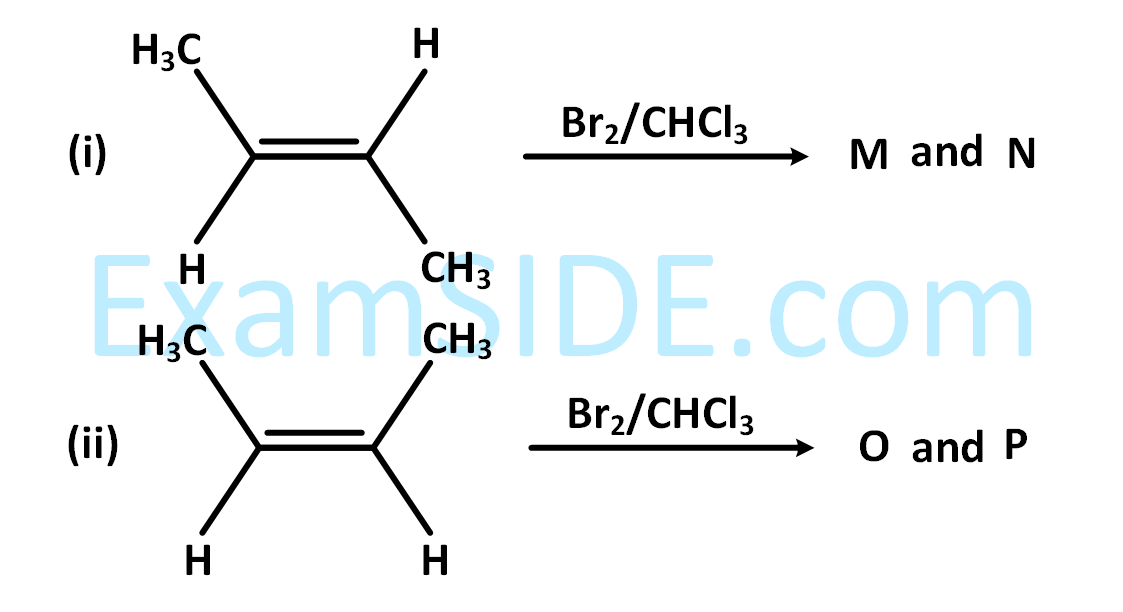
Among the following, the number of aromatic compound(s) is


3
The correct statement(s) about the oxoacids, $$HCl{O_4}$$ and $$HClO$$ is (are)
4
The color of the $${X_2}$$ molecules of group $$17$$ elements changes gradually from yellow to violet down the group. This is due to
5
A crystalline solid of a pure substance has a face-centered cubic structure with a cell edge of $$400$$ $$pm.$$ If the density of the substance in the crystal is $$8$$ $$g\,c{m^{ - 3}},$$ then the number of atoms present in $$256$$ $$g$$ of the crystal is $$N \times {10^{24}}.$$ The value of $$N$$ is
6
The conductance of a $$0.0015$$ $$M$$ aqueous solution of a weak monobasic acid was determined by using a conductivity cell consisting of platinized $$Pt$$ electrodes. The distance between the electrodes is $$120$$ $$cm$$ with an area of cross section of $$1$$ $$c{m^2}.$$ The conductance of this solution was found to be $$5 \times {10^{ - 7}}S.$$ The $$pH$$ of the solution is $$4.$$ The value of limiting molar conductivity $$\left( {\Lambda _m^o} \right)$$ of this weak monobasic acid in aqueous solution is $$Z \times {10^2}S$$ $$c{m^2}$$ $$mo{l^{ - 1}}.$$ The value of $$Z$$ is
7
Addition of excess aqueous ammonia to a pink colored aqueous solution of $$MC{l_2},6{H_2}O\left( X \right)$$ and $$N{H_4}Cl$$ gives an octahedral complex $$Y$$ in the presence of air. In aqueous solution, complex $$Y$$ behaves as $$1:3$$ electrolyte. The reaction of $$X$$ with excess $$HCl$$ at room temperature results in the formation of a blue colored complex $$Z.$$ The calculated spin only magnetic moment of $$X$$ and $$Z$$ is $$3.87$$ $$B.M.,$$ whereas it is zero for complex $$Y.$$ Among the following options, which statement(s) is (are) correct?
8
The sum of the number of lone pairs of electrons on each central atom in the following species is
$${[TeB{r_6}]^{2 - }},{\left[ {Br{F_2}} \right]^ + },SNF_3,$$ and $${\left[ {Xe{F_3}} \right]^ - }$$
(Atomic numbers: $$N = 7,F = 9,$$ $$S = 16,Br = 35,$$ $$Te = 52,Xe = 54$$)
$${[TeB{r_6}]^{2 - }},{\left[ {Br{F_2}} \right]^ + },SNF_3,$$ and $${\left[ {Xe{F_3}} \right]^ - }$$
(Atomic numbers: $$N = 7,F = 9,$$ $$S = 16,Br = 35,$$ $$Te = 52,Xe = 54$$)
9
Among $${H_2},H{e_2}^ + ,L{i_2},$$ $$B{e_2},{B_2},{C_2},{N_2},O_2^ - $$ and $${F_2},$$ the number of diamagnetic species is
(Atomic numbers : $$H = 1,He = 2,$$ $$Li = 3,Be = 4,$$ $$B = 5,C = 6,$$ $$N = 7,$$ $$O = 8,F = 9$$)
(Atomic numbers : $$H = 1,He = 2,$$ $$Li = 3,Be = 4,$$ $$B = 5,C = 6,$$ $$N = 7,$$ $$O = 8,F = 9$$)
10
For the synthesis of benzoic acid, the only CORRECT combination is
11
The IUPAC name(s) of the following compound is (are)


12
The correct statements(s) for the following addition reactions is (are)

13
For a solution formed by mixing liquids $$L$$ and $$M,$$ the vapor pressure of $$L$$ plotted against the mole fraction of $$M$$ in solution is shown in the following figure. Here $${X_L}$$ and $${X_M}$$ represent mole fractions of $$L$$ and $$M,$$ respectively, in the solution. The correct statement(s) applicable to this system is (are)


14
The only CORRECT combination in which the reaction proceeds through radical mechanism is :
15
The only CORRECT combination that gives two different carboxylic acids is :
16
For $$H{e^ + }$$ ion, the only INCORRECT combination is
17
For hydrogen atom, the only CORRECT combination is :
18
For the given orbital in Column 1, the only CORRECT combination for any hydrogen-like species is :
Mathematics
1
Let X and Y be two events such that $$P(X) = {1 \over 3}$$, $$P(X|Y) = {1 \over 2}$$ and $$P(Y|X) = {2 \over 5}$$. Then
2
Let f : R $$ \to $$ (0, 1) be a continuous function. Then, which of the following function(s) has (have) the value zero at some point in the interval (0, 1) ?
3
Let a, b, x and y be real numbers such that a $$-$$ b = 1 and y $$ \ne $$ 0. If the complex number z = x + iy satisfies $${\mathop{\rm Im}\nolimits} \left( {{{az + b} \over {z + 1}}} \right) = y$$, then which of the following is(are) possible value(s) of x?
4
If $$2x - y + 1 = 0$$ is a tangent to the hyperbola $${{{x^2}} \over {{a^2}}} - {{{y^2}} \over {16}} = 1$$ then which of the following CANNOT be sides of a right angled triangle?
5
Let [x] be the greatest integer less than or equals to x. Then, at which of the following point(s) the function $$f(x) = x\cos (\pi (x + [x]))$$ is discontinuous?
6
Which of the following is(are) NOT the square of a 3 $$ \times $$ 3 matrix with real entries?
7
If a chord, which is not a tangent, of the parabola y2 = 16x has the equation 2x + y = p, and mid-point (h, k), then which of the following is(are) possible value(s) of p, h and k?
8
For a real number $$\alpha $$, if the system
$$\left[ {\matrix{ 1 & \alpha & {{\alpha ^2}} \cr \alpha & 1 & \alpha \cr {{\alpha ^2}} & \alpha & 1 \cr } } \right]\left[ {\matrix{ x \cr y \cr z \cr } } \right] = \left[ {\matrix{ 1 \cr { - 1} \cr 1 \cr } } \right]$$
of linear equations, has infinitely many solutions, then 1 + $$\alpha $$ + $$\alpha $$2 =
$$\left[ {\matrix{ 1 & \alpha & {{\alpha ^2}} \cr \alpha & 1 & \alpha \cr {{\alpha ^2}} & \alpha & 1 \cr } } \right]\left[ {\matrix{ x \cr y \cr z \cr } } \right] = \left[ {\matrix{ 1 \cr { - 1} \cr 1 \cr } } \right]$$
of linear equations, has infinitely many solutions, then 1 + $$\alpha $$ + $$\alpha $$2 =
9
The sides of a right angled triangle are in arithmetic progression. If the triangle has area 24, then what is the length of its smallest side?
10
Let f : R $$ \to $$ R be a differentiable function such that f(0) = 0, $$f\left( {{\pi \over 2}} \right) = 3$$ and f'(0) = 1.
If $$g(x) = \int\limits_x^{\pi /2} {[f'(t)\text{cosec}\,t - \cot t\,\text{cosec}\,t\,f(t)]dt} $$
for $$x \in \left( {0,\,{\pi \over 2}} \right]$$, then $$\mathop {\lim }\limits_{x \to 0} g(x)$$ =
If $$g(x) = \int\limits_x^{\pi /2} {[f'(t)\text{cosec}\,t - \cot t\,\text{cosec}\,t\,f(t)]dt} $$
for $$x \in \left( {0,\,{\pi \over 2}} \right]$$, then $$\mathop {\lim }\limits_{x \to 0} g(x)$$ =
11
For how many values of p, the circle x2 + y2 + 2x + 4y $$-$$ p = 0 and the coordinate axes have exactly three common points?
12
Words of length 10 are formed using the letters A, B, C, D, E, F, G, H, I, J. Let x be the number of such words where no letter is repeated; and let y be the number of such words where exactly one letter is repeated twice and no other letter is repeated. Then, $${y \over {9x}}$$ = ?
13
For $$a = \sqrt 2 $$, if a tangent is drawn to a suitable conic (Column 1) at the point of contact ($$-$$1, 1), then which of the following options is the only CORRECT combination for obtaining its equation?
14
The tangent to a suitable conic (Column 1) at $$\left( {\sqrt 3 ,\,{1 \over 2}} \right)$$ is found to be $$\sqrt 3 x + 2y = 4$$, then which of the following options is the only CORRECT combination?
15
If a tangent to a suitable conic (Column 1) is found to be y = x + 8 and its point of contact is (8, 16), then which of the following options is the only CORRECT combination?
16
Which of the following options is the only INCORRECT combination?
17
Which of the following options is the only CORRECT combination?
18
Which of the following options is the only CORRECT combination?
Physics
1
A stationary source emits sound of frequency $${f_0} = 492\,Hz.$$ The sound is reflected by a large car approaching the source with a speed of $$2\,m{s^{ - 1.}}$$ The reflected signal is received by the source and superposed with the original.
What will be the beat frequency of the resulting signal in $$Hz$$? (Given that the speed of sound in air is $$330\,m{s^{ - 1}}$$ and the car reflects the sound at the frequency it has received).
What will be the beat frequency of the resulting signal in $$Hz$$? (Given that the speed of sound in air is $$330\,m{s^{ - 1}}$$ and the car reflects the sound at the frequency it has received).
2
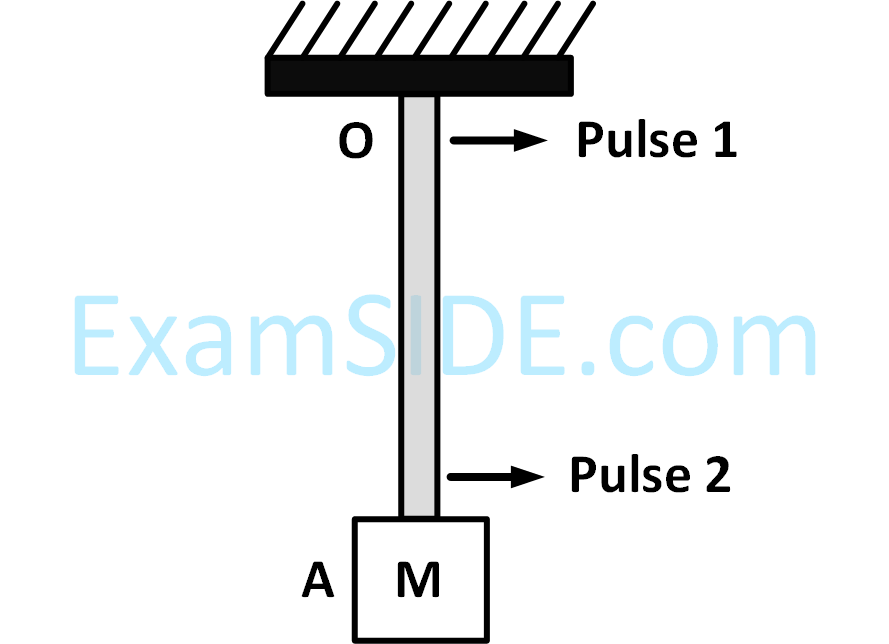
A block $$M$$ hangs vertically at the bottom end of a uniform rope of constant mass per unit length. The top end of the rope is attached to fixed rigid support at $$O.$$ A transverse wave pulse (Pulse 1) of wavelength $${\lambda _0}$$ is produced at point $$O$$ on the rope. The pulse takes time $${T_{OA}}$$ to reach point $$A.$$ If the wave pulse of wavelength $${\lambda _0}$$ is produced at point $$A$$ (Pulse 2) without disturbing the position of $$M$$ it takes time $${T_{AO}}$$ to reach point $$O.$$ which of the following options is/are correct?

3
A block of mass $$M$$ has a circular cut with a frictionless surface as shown. The block resets on the horizontal frictionless surface of a fixed table. Initially the right edge of the block is at $$x=0,$$ in a co-ordinate system fixed to the table. A point mass $$m$$ is released from rest at the topmost point of the path as shown and it slides down.
When the mass loses contact with the block, its position is $$x$$ and the velocity is $$v.$$ At that instant, which of the following options is/are correct?

When the mass loses contact with the block, its position is $$x$$ and the velocity is $$v.$$ At that instant, which of the following options is/are correct?

4
A human body has a surface area of approximately $$1\,m{}^2.$$ The normal body temperature is $$10$$ $$K$$ above the surrounding room temperature $${T_0}.$$ Take the room temperature to be $${T_0} = 300K.$$ For $${T_0} = 300\,K,$$ the value of $$\sigma T_0^4 = 460\,W{m^{ - 2}}$$ (where $$\sigma $$ is the Stefan-Boltzmann constant).
Which of the following options is / are correct?
Which of the following options is / are correct?
5
A circular insulated copper wire loop is twisted to form two loops of area $$A$$ and $$2A$$ as shown in the figure. At the point of crossing the wires remain electrically insulated from each other. The entire loop lies in the plane (of the paper). A uniform magnetic field $$\overrightarrow B $$ points into the plane of the paper. At $$t=0,$$ the loop starts rotating about the common diameter as axis with a constant angular velocity $$\omega $$ in the magnetic field.
Which of the following options is/are correct?
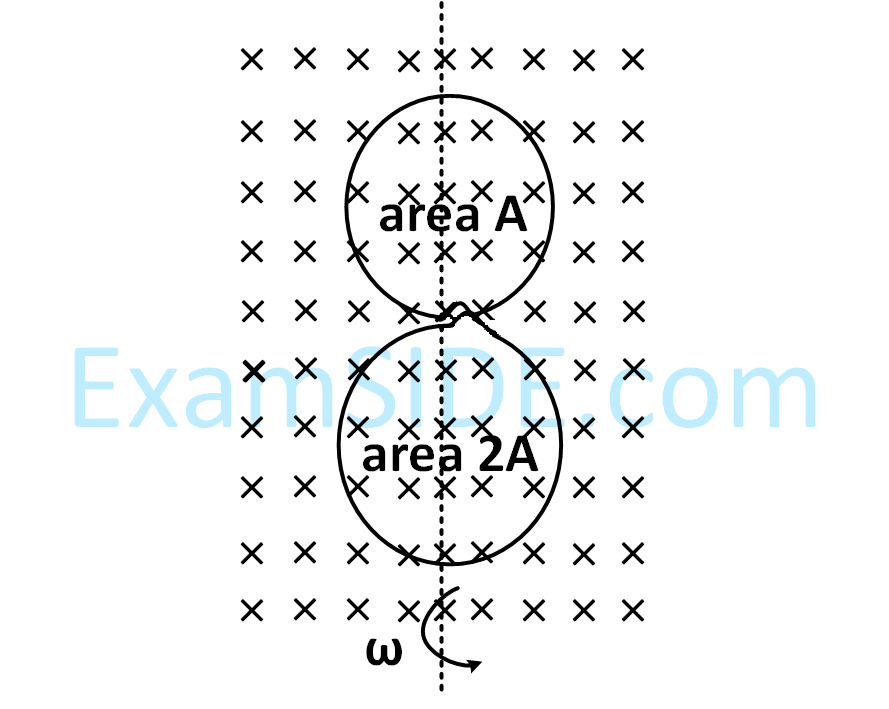
Which of the following options is/are correct?

6
For an isosceles prism of angle $$A$$ and refractive index $$\mu $$, it is found that the angle of minimum deviation $${\delta _m} = A.$$
Which of the following options is/are correct?
Which of the following options is/are correct?
7
In the circuit shown, $$L = 1\,\mu H,C = 1\,\mu F\,$$ and $$R = 1\,k\Omega .$$ They are connected in series with an a.c. source
$$V = {V_0}\sin \omega t$$ as shown.
Which of the following options is/are correct?

Which of the following options is/are correct?

8
A drop of liquid of radius $$R = {10^{ - 2}}\,m$$ having surface tension $$S = {{0.1} \over {4\pi }}N{m^{ - 1}}$$ divides itself into $$K$$ identical drops. In this process the total change in the surface energy $$\Delta U = {10^{ - 3}}\,J.$$ If $$K = {10^\alpha }$$ then the value of $$\alpha $$ is
9
An electron in a hydrogen atom undergoes a transition from an orbit with quantum number $${n_i}$$ to another with quantum number $${n_f}$$. $${V_i}$$ and $${V_f}$$ are respectively the initial and final potential energies of the electron. If $${{{V_i}} \over {{V_f}}} = 6.25$$, then the smallest possible $${n_f}$$ is
10
In which case will the particle move in a straight line with constant velocity?
11
$${}^{131}{\rm I}$$ is an isotope of Iodine that $$B$$ decays to an isotope of Xenon with a half-life of $$8$$ days. A small amount of a serum labelled with $${}^{131}{\rm I}$$ is injected into the blood of a person. The activity of the amount of $${}^{131}{\rm I}$$ injected was $$2.4 \times {10^5}$$ Becquerel $$(Bq).$$ It is known that the injected serum will get distributed uniformly in the blood stream in less than half an hour. After $$11.5$$ hours, $$2.5$$ ml of blood is drawn from person's body, and gives an activity of $$115$$ $$Bq$$. The total volume of blood in the person's body, in liters is approximately (you may use $${e^x} \approx 1 + x\,\,$$ for $$\left| x \right| < < 1$$ and $$\ln 2 \approx 0.7).$$
12
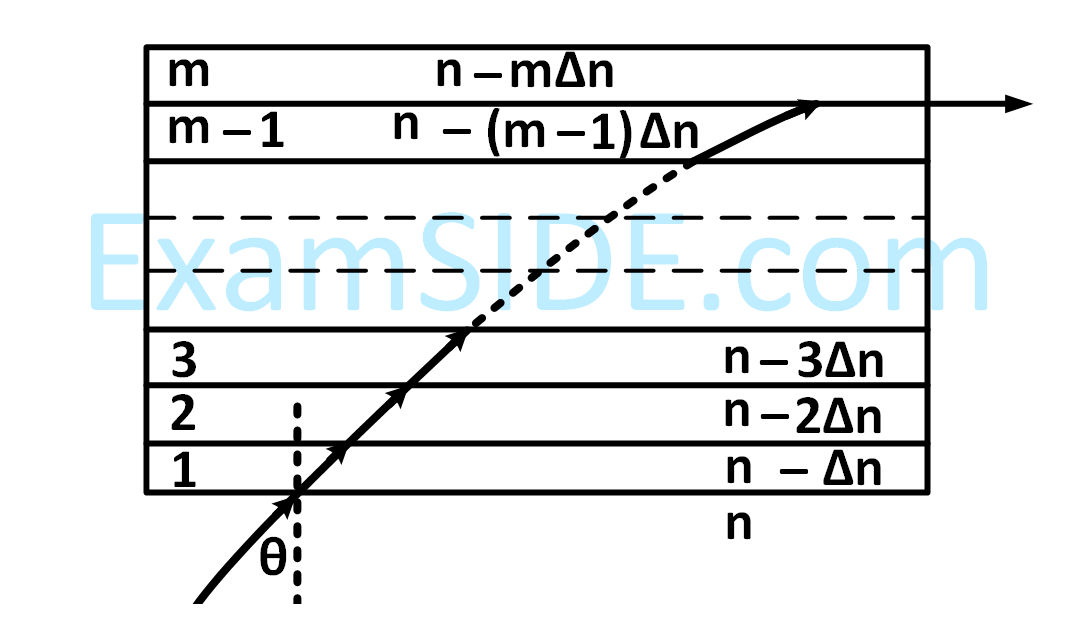
A monochromatic light is travelling in a medium of refractive index $$n=1.6.$$ It enters a stack of glass layers from the bottom side at an angle $$\theta = {30^ \circ }.$$ The interfaces of the glass layers are parallel to each other. The refractive indices of different glass layers are monotonically decreasing as $${n_m} = n - m\Delta n,$$ where $${n_m}$$ is the refractive index of the $${m^{th}}$$ slab and $$\Delta n = 0.1$$ (see the figure). The ray is refracted out parallel to the interface between the $${\left( {m - 1} \right)^{th}}$$ and $${m^{th}}$$ slabs from the right side of the stack. What is the value of $$m$$?

13
In which case will the particle describe a helical path with axis along the positive $$z$$ direction?
14
In which case would the particle move in a straight line along the negative direction of $$y$$-axis (i.e., move along $$ - \widehat y$$)?
15
Which of the following options is the only correct representation of a process in which
$$\Delta U = \Delta Q - P\Delta V$$?
$$\Delta U = \Delta Q - P\Delta V$$?
16
Which one of the following options is the correct combination?
17
Which one of the following options correctly represents a thermodynamic process that is used as a correction in the determination of the speed of sound in an ideal gas?
18
A flat plate is moving normal to its plane through a gas under the reaction of a constant force $$F.$$ The gas is kept at a very low pressure. The speed of the plate $$v$$ is much less than the average speed u of the gas molecules.
Which of the following options is /are true?
Which of the following options is /are true?