For a first-order reaction A $$\to$$ P, the temperature (T) dependent rate constant (k) was found to follow the equation $$\log k = - (2000){1 \over T} + 6.0$$. The pre-exponential factor A and activation energy $$E_a$$, respectively, are
The spin only magnetic moment value (in Bohr magneton units) of Cr(CO)$$_6$$ is
In the following carbocation, H/CH$$_3$$ that is most likely to migrate to the positively charged carbon is :

The correct stability order of the following resonance structures is

For the reduction of NO$$_3^ - $$ ion in an aqueous solution, E$$^0$$ is + 0.96 V. Values of E$$^0$$ for some metal ions are given below:
$$\matrix{ {{V^{2 + }}(aq.) + 2{e^ - } \to V} & {{E^0} = - 1.19\,V} \cr {F{e^{3 + }}(aq.) + 3{e^ - } \to Fe} & {{E^0} = - 0.04\,V} \cr {A{u^{3 + }}(aq) + 3{e^ - } \to Au} & {{E^0} = + 1.40\,V} \cr {H{g^{2 + }}(aq) + 2{e^ - } \to Hg} & {{E^0} = + 0.86\,V} \cr } $$
The pair(s) of metals that is (are) oxidized by NO$$_3^ - $$ in aqueous solution is(are)
Among the following, the state function(s) is(are)
In the reaction
$$\mathrm{2X+B_2H_6\to[BH_2(X)_2]^+[BH_4]^-}$$
the amine(s) X is(are) :
The nitrogen oxide(s) that contain(s) N-N bond(s) is(are)
The correct statement(s) about the following sugar X and Y is(are)


Match each of the reactions given in Column I with the corresponding product(s) given in Column II:
| Column I | Column II | ||
|---|---|---|---|
| (A) | $$\mathrm{Cu+dil.~HNO_3}$$ | (P) | $$\mathrm{NO}$$ |
| (B) | $$\mathrm{Cu+conc.~HNO_3}$$ | (Q) | $$\mathrm{NO_2}$$ |
| (C) | $$\mathrm{Zn+dil.~HNO_3}$$ | (R) | $$\mathrm{N_2O}$$ |
| (D) | $$\mathrm{Zn+conc.~HNO_3}$$ | (S) | $$\mathrm{Cu(NO_3)_2}$$ |
| (T) | $$\mathrm{Zn(NO_3)_2}$$ |
Match each of the compounds given in Column I with the reaction(s), that they can undergo, given in Column II.
| Column I | Column II | ||
|---|---|---|---|
| (A) |  |
(P) | Nucleophilic substitution |
| (B) |  |
(Q) | Elimination |
| (C) |  |
(R) | Nucleophilic addition |
| (D) |  |
(S) | Esterification with acetic anhydride |
| (T) | Dehydrogenation |
In a constant volume calorimeter, 3.5 g of a gas with molecular weight 28 was burnt in excess oxygen at 298.0 K. The temperature of the calorimeter was found to increase from 298.0 K to 298.45 K due to the combustion process. Given that the heat capacity of the calorimeter is 2.5 kJ K$$^{-1}$$, the numerical value for the enthalpy of combustion of the gas in kJ mol$$^{-1}$$ is ____________.
At 400 K, the root mean square (rms) speed of a gas X (molecular weight = 40) is equal to the most probable speed of gas Y at 60 K. The molecular weight of the gas Y is ___________.
The dissociation constant of a substituted benzoic acid at 25$$^\circ$$C is 1.0 $$\times$$ 10$$^{-4}$$. The pH of a 0.01 M solution of its sodium salt is __________.
The total number of $$\alpha$$ and $$\beta$$ particles emitted in the nuclear reaction $$_{92}^{238}U \to _{82}^{214}Pb$$ is _________.
The oxidation number of Mn in the product of alkaline oxidative fusion of MnO$$_2$$ is ___________.
The number of water molecule(s) directly bonded to the centre in CuSO$$_4$$ . 5H$$_2$$O is __________.
The coordination number of Al in the crystalline state of AlCl$$_3$$ is ___________.
The total number of cyclic structural as well as stereoisomers possible for a compound with the molecular formula C$$_5$$H$$_{10}$$ is ____________.
Let $$f:R \to R$$ be a continuous function which satisfies $$f(x) = \int\limits_0^x {f(t)dt} $$. Then, the value of $$f(\ln 5)$$ is ____________.
Match the statements/expressions in Column I with the values given in Column II:
| Column I | Column II | ||
|---|---|---|---|
| (A) | The number of solutions of the equation $$x{e^{\sin x}} - \cos x = 0$$ in the interval $$\left( {0,{\pi \over 2}} \right)$$ | (P) | 1 |
| (B) | Value(s) of $$k$$ for which the planes $$kx + 4y + z = 0,4x + ky + 2z = 0$$ and $$2x + 2y + z = 0$$ intersect in a straight line | (Q) | 2 |
| (C) | Value(s) of $$k$$ for which $$|x - 1| + |x - 2| + |x + 1| + |x + 2| = 4k$$ has integer solution(s) | (R) | 3 |
| (D) | If $$y' = y + 1$$ and $$y(0) = 1$$ then value(s) of $$y(\ln 2)$$ | (S) | 4 |
| (T) | 5 |
Match the statements/expressions in Column I with the values given in Column II:
| Column I | Column II | ||
|---|---|---|---|
| (A) | Root(s) of the expression $$2{\sin ^2}\theta + {\sin ^2}2\theta = 2$$ | (P) | $${\pi \over 6}$$ |
| (B) | Points of discontinuity of the function $$f(x) = \left[ {{{6x} \over \pi }} \right]\cos \left[ {{{3x} \over \pi }} \right]$$, where $$[y]$$ denotes the largest integer less than or equal to y | (Q) | $${\pi \over 4}$$ |
| (C) | Volume of the parallelopiped with its edges represented by the vectors $$\widehat i + \widehat j + \widehat i + 2\widehat j$$ and $$\widehat i + \widehat j + \pi \widehat k$$ | (R) | $${\pi \over 3}$$ |
| (D) | Angle between vectors $$\overrightarrow a $$ and $$\overrightarrow b $$ where $$\overrightarrow a $$, $$\overrightarrow b $$ and $$\overrightarrow c $$ are unit vectors satisfying $$\overrightarrow a + \overrightarrow b + \sqrt 3 \overrightarrow c = \overrightarrow 0 $$ | (S) | $${\pi \over 2}$$ |
| (T) | $$\pi $$ |
A line with positive direction cosines passes through the point P(2, $$-$$1, 2) and makes equal angles with the coordinate axes. The line meets the plane $$2x + y + z = 9$$ at point Q. The length of the line segment PQ equals
If $${I_n} = \int\limits_{ - \pi }^\pi {{{\sin nx} \over {(1 + {\pi ^x})\sin x}}dx,n = 0,1,2,} $$ .... then
The maximum value of the function $$f(x) = 2{x^3} - 15{x^2} + 36x - 48$$ on the set $$A = \{ x|{x^2} + 20 \le 9x|\} $$ is __________.
$$x = 1,2$$ and $$\mathop {\lim }\limits_{x \to 0} \left( {1 + {{p\left( x \right)} \over {{x^2}}}} \right) = 2$$.
Then the value of $$p (2)$$ is
If the function $$f(x) = {x^3} + {e^{x/2}}$$ and $$g(x) = {f^{ - 1}}(x)$$, then the value of $$g'(1)$$ is _________.
Then the number of such points for which $$x^2 + {y^2} + {z^2} \le 100$$ is
If the sum of first $$n$$ terms of an A.P. is $$c{n^2}$$, then the sum of squares of these $$n$$ terms is
Let ABC and ABC' be two non-congruent triangles with sides AB = 4, AC = AC' = 2$$\sqrt2$$ and angle B = 30$$^\circ$$. The absolute value of the difference between the areas of these triangles is ___________.
The locus of the orthocentre of the triangle formed by the lines
$$(1 + p)x - py + p(1 + p) = 0,
$$
$$(1 + q)x - qy + q(1 + q) = 0$$
and $$y = 0$$, where $$p \ne q$$, is :
Photoelectric effect experiments are performed using three different metal plates p, q and r having work functions $$\phi_p=2.0~\mathrm{eV}$$, $$\phi_q=2.5~\mathrm{eV}$$ and $$\phi_r=3.0~\mathrm{eV}$$, respecticely. A light beam containing wavelengths of 550 nm, 450 nm and 350 nm with equal intensities illuminates each of the plates. The correct I-V graph for the experiment is (Take hc = 1240 eV nm)
The mass M shown in the figure below oscillates in simple harmonic motion with amplitude A. The amplitude of the point P is

A uniform rod of length L and mass M is pivoted at the centre. Its two ends are attached to two springs of equal spring constants $$k$$. The springs are fixed to rigid supports as shown in the figure, and the rod is free to oscillate in the horizontal plane. The rod is gently pushed through a small angle $$\theta$$ in one direction and released. The frequency of oscillation is

The figure shows the PV plot of an ideal gas taken through a cycle ABCDA. The part ABC is a semicircle and CDA is half of an ellipse. Then,

Under the influence of the Coulomb field of charge +Q, a charge $$-$$q is moving around it in an elliptical orbit. Find out the correct statement(s):
Two metallic rings A and B, identical in shape and size but having different resistivities $$\rho_A$$ and $$\rho_B$$, are kept on top of two identical solenoids as shown in the figure below. When current I is switched on in both the solenoids in identical manner, the rings A and B jump to heights $$h_A$$ and $$h_B$$, respectively, with $$h_A > h_B$$. The possible relation(s) between their resistivities and their masses $$m_A$$ and $$m_B$$ is (are)

A sphere is rolling without slipping on a fixed horizontal plane surface. In the figure below, A is the point of contact, B is the centre of the sphere and C is its topmost point. Then,

A student performed the experiment to measure the speed of sound in air using resonance air-column method. Two resonances in the air-column were obtained by lowering the water level. The resonance with the shorter air-column is the first resonance and that with the longer air-column is the second resonance. Then,
Column II gives certain systems undergoing a process. Column I suggests changes in some of the parameters related to the system. Match the statements in Column I to the appropriate process(es) from Column II:
| Column I | Column II | ||
|---|---|---|---|
| (A) | The energy of the system is increased. | (P) | System : A capacitor, initially uncharged. Process : It is connected to a battery. |
| (B) | Mechanical energy is provided to the system, which is converted into energy of random motion of its parts. | (Q) | System : A gas in an adiabatic container filled with an adiabatic piston. Process : The gas is compressed by pushing the piston. |
| (C) | Internal energy of the system is converted into its mechanical energy. | (R) | System : A gas in a rigid container. Process : The gas gets cooled due to colder atmosphere surrounding it. |
| (D) | Mass of the system is decreased. | (S) | System : A heavy nucleus, initially at rest. Process : The nucleus fissions into two fragments of nearly equal masses and some neutrons are emitted. |
| (T) | System : A resistive wire loop. Process : The loop is placed in a time varying magnetic field perpendicular to its plane. |
Column I shows four situations of standard Young's double slit arrangement with the screen placed far away from the slits S$$_1$$ and S$$_2$$. In each of these cases, S$$_1$$P$$_0$$ = S$$_2$$P$$_0$$, S$$_1$$P$$_1$$ $$-$$ S$$_2$$P$$_1$$ = $$\lambda/4$$ and S$$_1$$P$$_2$$ $$-$$ S$$_2$$P$$_2$$ = $$\lambda/3$$, where $$\lambda$$ is the wavelength of the light used. In the cases B, C and D, a transparent sheet of refractive index $$\mu$$ and thickness t is pasted on slit S$$_2$$. The thickness of the sheets are different in different cases. The phase difference between the light waves reaching a point P on the screen from the two slits is denoted by $$\delta$$(P) and the intensity by I(P). Match each situation given in Column I with the statement(s) in Column II valid for that situation:
| Column I | Column II | ||
|---|---|---|---|
| (A) |  |
(P) | $$\delta ({P_0}) = 0$$ |
| (B) | $$(\mu-1)t=\lambda/4$$ |
(Q) | $$\delta ({P_1}) = 0$$ |
| (C) | $$(\mu-1)t=\lambda/2$$ |
(R) | $$I({P_1}) = 0$$ |
| (D) | $$(\mu-1)t=3\lambda/4$$ |
(S) | $$I({P_0}) > I({P_1})$$ |
| (T) | $$I({P_2}) > I({P_1})$$ |
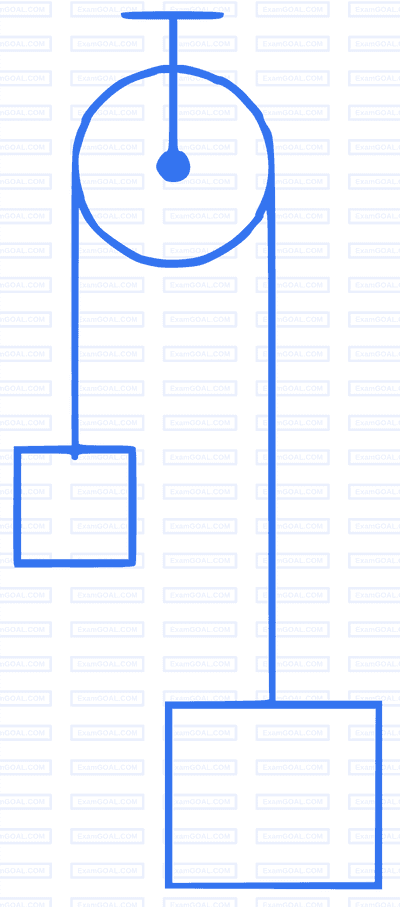
A light inextensible string that goes over a smooth fixed pulley as shown in the figure connects two blocks of masses 0.36 kg and 0.72 kg. Taking g = 10 m/s2, find the work done (in joules) by the string on the block of mass 0.36 kg during the first second after the system is released from rest.
Two soap bubbles A and B are kept in a closed chamber where the air is maintained at pressure 8 N/m$$^2$$. The radii of bubbles A and B are 2 cm and 4 cm, respectively. Surface tension of the soap-water used to make bubbles is 0.04 N/m. Find the ratio $$n_B/n_A$$, where $$n_A$$ and $$n_B$$ are the number of moles of air in bubbles A and B, respectively. (Neglect the effect of gravity.)
A steady current I goes through a wire loop PQR having shape of a right angle triangle wit6h PQ = 3, PR = 4x and QR = 5x. If the magnitude of the magnetic field at P due to this loop is $$k\left( {{{{\mu _0}I} \over {48\pi x}}} \right)$$, find the value of $$k$$.
A cylindrical vessel of height 500 mm has an orifice (small hole) at its bottom. The orifice is initially closed and water is filled in it up to height H. Now the top is completely sealed with a cap and the orifice at the bottom is opened. Some water comes out from the orifice and the water level in the vessel becomes steady with height of water column being 200 mm. Find the fall in height (in mm) of water level due to opening of the orifice. (Take atmospheric pressure = 1.0 $$\times$$ 10$$^5$$ N/m$$^2$$, density of water = 1000 kg/m$$^3$$ and g = 10 m/s$$^2$$. Neglect any effect of surface tension.)
A 20 cm long string, having a mass of 1.0 g, is fixed at both the ends. The tension in the string is 0.5 N. The string is set into vibrations using an external vibrator of frequency 100 Hz. find the separation (in cm) between the successive nodes on the string.
A solid sphere of radius R has a charge Q distributed in its volume with a charge density $$\rho = K{r^a}$$, where K and a are constants and r is the distance from its centre. If the electric field at $$r = R/2$$ is 1/8 times than at $$r = R$$, find the value of $$a$$.
A metal rod AB of length 10x has its one end A in ice at 0$$^\circ$$C and the other end B in water at 100$$^\circ$$C. If a point P on the rod is maintained at 400$$^\circ$$C, then it is found that equal amounts of water and ice evaporate and melt per unit time. The latent heat of evaporation of water is 540 cal/g and latent heat of melting of ice is 80 cal/g. If the point P is at a distance of $$\lambda x$$ from the ice end A, find the value of $$\lambda$$. (Neglect any heat loss to the surrounding.)
Three objects A, B and C are kept in a straight line on a frictionless horizontal surface. These have masses m, 2m and m, respectively. The object A moves towards B with a speed 9 m/s and makes an elastic collision with it. Thereafter, B makes completely inelastic collision with C. All motions occur on the same straight line. Find the final speed (in m/s) of the object C.