Consider the oscillator circuit shown in the figure. The function of the network (shown in dotted lines) consisting of the 100 k $$\Omega$$ resistor in series with the two diodes connected back- to is to:

Consider the constant current source shown in the figure below. Let $$\beta $$ represent the current gain of the transistor

The load current I₀ through R_L is

The following signal V_i of peak voltage 8V is applied to the non-inverting terminal of an ideal Opamp. The transistor has V_BE = 0.7 V, $$\beta \, = \,100;$$ V_LED = 1.5 V, V_CC = 10V and -V_CC = -10V.

The number of times the LED glows is ______.

An ideal opamp has voltage source V₁, V₃, V₅, ......, V_N-1, connected to the non- inverting input and V₂, V₄, V₆, .....V_N connected to the inverting input as shown in the figure below (+V_CC= 15 volt, -V_CC = -15 volt). The voltage V₁, V₂, V₃,V₄, V₅, V₆ ....... are 1, -1/2, 1/3, -1/4, 1/5, -1/6, .... volt, respectively. As N approaches infinity, the output voltage (in volt) is _______

A p-i-n photo diode of responsivity 0.8A/W is connected to the inverting input of an ideal opamp as shown in the figure, +V_CC = 15V, - V_CC = -15V, Load resistor R_L = 10 k$$\Omega $$ . If 10$$\mu $$W of power is incident on the photodiode, then the value of the photocurrent (in $$\mu $$A) through the load is _____.

Consider binary data transmission at a rate of 56 kbps using baseband binary pulse amplitude modulation (PAM) that is designed to have a raised-cosine spectrum. The transmission bandwidth (in kHz) required for a roll-off factor of 0.25 is ______.

An antenna pointing in a certain direction has a noise temperature of 50K. The ambient temperature is 290K. The antenna is connected to a pre-amplifier that has a noise figure of 2dB and an available gain of 40 dB over an effective bandwidth of 12 MHz. The effective input noise temperature T_e for the amplifier and the noise power P_ao at the output of the preamplifier, respectively, are

Consider a discreet memoryless source with alphabet $$S = \left\{ {{s_0},\,{s_1},\,{s_2},\,{s_3},\,{s_{4......}}} \right\}$$ and respective probabilities of occurrence $$P = \left\{ {{1 \over 2},\,{1 \over 4},\,{1 \over 8},\,{1 \over {16}},\,{1 \over {32}},......} \right\}$$. The entropy of the source (in bits) is__________.

A digital communication system uses a repetition code for channel encoding/decoding. During transmission, each bit is repeated three times (0 is transmitted as 000, and 1 is transmitted as 111). It is assumed that the source puts out symbols independently and with equal probability. The decoder operates as follows: In a block of three received bits, if the number of zeros exceeds the number of ones, the decoder decides in favor of a 0, and if the number of ones exceeds the number of zeros, the decoder decides in favor of a 1, Assuming a binary symmetric channel with crossover probability p = 0.1, the average probability of error is _______

An analog pulse s(t) is transmitted over an additive white Gaussian noise (AWGN) channel. The received signal is r(t) = s(t) + n(t), where n(t) is additive white Gaussian noise with power spectral density $${{{N_0}} \over 2}$$. The received signal is passed through a filter with impulse response h(t). Let $${E_s}$$ and $${E_n}$$ denote the energies of the pulse s(t) and the filter h(t), respectively. When the signal-to-noise ratio (SNR) is maximized at the output of the filter $$\left( {SN{R_{\max }}} \right)$$, which of the following holds?

A super heterodyne receiver operates in the frequency range of 58 MHz – 68 MHz. The intermediate frequency f_1F and local oscillator frequency f_L0 are chosen such that f_1F $$\leq$$ f_L0.It is required that the image frequencies fall outside the 58 MHz – 68 MHz band. The minimum required f_1F (in MHz) is ___________.

The open-loop transfer function of a unity-feedback control system is $$$G\left(S\right)\;=\frac K{s(s\;+\;2)}$$$ For the peak overshoot of the closed-loop system to a unit step input to be 10%, the value of K is __________.

Match the inferences X, Y, and Z, about a system, to the corresponding properties of the elements of first column in Routh's Table of the system characteristic equation.

X: The system is stable …
Y: The system is unstable …
Z: The test breaks down …

P: … when all elements are positive
Q: … when any one element is zero
R: … when there is a change in sign of coefficients

The open-loop transfer function of a unity-feedback control system is $$$G\left(s\right)=\frac K{s^2+5s+5}$$$ The value of K at the breakaway point of the feedback control system's root-locus plot is _____________

The transfer function of a linear time invariant system is given by $$H\left(s\right)\;=\;2s^4\;-\;5s^3\;+\;5s\;-\;2$$. The number of zeros in the right half of the s-plane is __________.

A closed-loop control system is stable if the Nyquist plot of the corresponding open-loop transfer function

The output of the combinational circuit given below is

Identify the circuit below.

The functionality implemented by the circuit below is

The electric field of a uniform plane wave travelling along the negative $$z$$ direction is given by the following equation: $$$\overrightarrow E {}_w^i = \left( {{{\widehat a}_{_x}} + j{{\widehat a}_{_y}}} \right){E_0}{e^{jkz}}$$$

This wave is incident upon a receiving antenna placed at the origin and whose radiated electric field towards the incident wave is given by the following equation:

$$${\overrightarrow E _{_a}} = \left( {{{\widehat a}_{_x}} + 2{{\widehat a}_{_y}}} \right){E_1}{1 \over r}{e^{ - jkr}}$$$

The polarization of the incident wave, the polarization of the antenna and losses due to the polarization mismatch are, respectively,

The propagation constant of a lossy transmission line is (2 + j5) $${m^{ - 1}}$$ and its characteristic impedance is (50 + j0) $$\Omega $$ at $$\omega = \,{10^6}\,rad\,{S^{ - 1}}$$. The values of the line constants L, C, R, G are, respectively,

An antenna pointing in a certain direction has a noise temperature of $$50K$$. The ambient temperature is $$290K$$. The antenna is connected to a pre-amplifier that has a noise figure of 2 dB and an available gain of 40 dB over an effective bandwidth of $$12$$ $$MHz$$. The effective input noise temperature $${T_e}$$ for the amplifier and the noise power $${P_{ao}}$$ at the output of the preamplifier, respectively, are

Two lossless X-band horn antennas are separated by a distance of $$200\lambda $$. The amplitude reflection coefficients at the terminals of the transmitting and receiving antennas are $$0.15$$ and $$0.18$$, respectively. The maximum directivities of the transmitting and receiving antennas (over the isotropic antenna) are $$18$$ $$dB$$ and $$22$$ $$dB$$, respectively. Assuming that the input power in the lossless transmission line connected to the antenna is $$2$$ $$W$$, and that the antennas are perfectly aligned and polarization matched, the power ( in mW) delivered to the load at the receiver is ________ .

The far-zone power density radiated by a helical antenna is approximated as: $$$\overrightarrow W {\,_{rad}} = \overrightarrow W \,average\, \approx \,\widehat a{}_rC{}_0\,{1 \over {{r^2}}}{\cos ^4}\theta $$$

The radiated power density is symmetrical with respect to $$\phi $$ and exists only in the upper hemisphere: $$0 \le \theta \le {\pi \over 2};\,\,\,\,0 \le \theta \le 2\pi ;$$

$${C_0}$$ is a constant. The power radiated by the antenna (in watts) and the maximum directivity of the antenna, respectively, are

Concentric spherical shells of radii 2 m, 4 m, and 8 m carry uniform surface charge densities of 20 nC/m² , −4 nC/m² and ρ_s ,respectively. The value of ρ_s (nC/m²) required to ensure that the electric flux density $$\overrightarrow D=\overrightarrow0$$ at radius 10 m is _________.

What is the voltage V_out in the following circuit?

A small percentage of impurity is added to an intrinsic semiconductor at 300 K. Which one of the following statements is true for the energy band diagram shown in the following figure?

Consider the following statements for a metal oxide semiconductor field effect transistor (MOSFET):

P: As channel length reduces, OFF-state current increases.
Q:As channel length reduces, output resistance increases.
R: As channel length reduces, threshold voltage remains constant.
S: As channel length reduces, ON current increases.

Which of the above statements are INCORRECT?

Consider an n-channel metal oxide semiconductor field effect transistor (MOSFET) with a gate-to-source voltage of 1.8 V. Assume that $${W \over L} = 4,{\mu _{\rm N}}{C_{ox}} = 70 \times {10^{ - 6}}{\rm A}{V^{ - 2}}$$ , the threshold voltage is 0.3V, and the channel length modulation parameter is 0.09 V^-1, In the saturation region, the drain conductance (in micro siemens) is__________.

Let $${M^4} = {\rm I}$$ (where $${\rm I}$$ denotes the identity matrix) and $$M \ne {\rm I},\,\,{M^2} \ne {\rm I}$$ and $${M^3} \ne {\rm I}$$. Then, for any natural number $$k, $$ $${M^{ - 1}}$$ equals:

A sequence $$x\left[ n \right]$$ is specified as $$$\left[ {\matrix{ {x\left[ n \right]} \cr {x\left[ {n - 1} \right]} \cr } } \right] = {\left[ {\matrix{ 1 & 1 \cr 1 & 0 \cr } } \right]^n}\left[ {\matrix{ 1 \cr 0 \cr } } \right],\,\,for\,\,n \ge 2.$$$
The initial conditions are $$x\left[ 0 \right] = 1,\,\,x\left[ 1 \right] = 1$$ and $$x\left[ n \right] = 0$$ for $$n < 0.$$ The value of $$x\left[ {12} \right]$$ is __________.

The integral $$\,\,{1 \over {2\pi }}\int {\int_D {\left( {x + y + 10} \right)dxdy\,\,} } $$ where $$D$$ denotes the disc: $${x^2} + {y^2} \le 4,$$ evaluates to _________.

Given the following statements about a function $$f:R \to R,$$ select the right option:
$$P:$$ If $$f(x)$$ is continuous at $$x = {x_0},$$ then it is also differentiable at $$x = {x_0},$$
$$Q:$$ If $$f(x)$$ is continuous at $$x = {x_0},$$ then it may not be differentiable at $$x = {x_0},$$
$$R:$$ If $$f(x)$$ is differentiable at $$x = {x_0},$$ then it is also continuous at $$x = {x_0},$$

The region specified by
$$\left\{ {\left( {\rho ,\varphi ,{\rm Z}} \right):3 \le \rho \le 5,\,\,{\pi \over 8} \le \phi \le {\pi \over 4},\,\,3 \le z \le 4.5} \right\}$$ in cylindrical coordinates has volume of ___________.

The second moment of a Poisson-distributed random variables is $$2.$$ The mean of the random variable is _______.

Two random variables $$X$$ and $$Y$$ are distributed according to $$${f_{X,Y}}\left( {x,y} \right) = \left\{ {\matrix{ {\left( {x + y} \right),} & {0 \le x \le 1,} & {0 \le y \le 1} \cr {0,} & {otherwise} & \, \cr } } \right.$$$

The probability $$P\left( {X + Y \le 1} \right)$$ is ________.

In an 8085 system, a PUSH operation requires more clock cycles than a POP operation. Which one of the following options is the correct reason for this?

A network consisting of a finite number of linear resistor (R), inductor (L), and capacitor (C) elements, connected all in series or all in parallel, is excited with a source of the form
$$\sum\limits_{k = 1}^3 {{a_k}\,\,\cos \,\left( {k{\omega _0}t} \right),\,\,\,} $$ where $${a_k} \ne 0,\,\,{\omega _0} \ne 0$$.

The source has nonzero impedance. Which one of the following is a possible form of the output measured across a resistor in the network?

An AC voltage source V = 10 sin(t) volts is applied to the following network. Assume that R₁ = 3 kΩ, R₂ = 6 kΩ and R₃ = 9 kΩ and that the diode is ideal.

RMS current I_rms (in mA) through the diode is _________.

Consider a two-port network with the transmission matrix: T = $$\begin{bmatrix}A&B\\C&D\end{bmatrix}$$. If the network is reciprocal, then

In the circuit shown in the figure, the maximum power (in watt) delivered to the resistor R is _________.

A sequence x$$\left[ n \right]$$ is specified as $$\left[ {\matrix{ {x\left[ n \right]} \cr {x\left[ {n - 1} \right]} \cr } } \right] = {\left[ {\matrix{ 1 \cr 1 \cr } \,\matrix{ 1 \cr 0 \cr } } \right]^n}\left[ {\matrix{ 1 \cr 0 \cr } } \right]$$, for n $$ \ge $$2.
The initial conditions are x$$\left[ 0 \right]$$ = 1, x$$\left[ 1 \right]$$=1 and x$$\left[ n \right]$$=0 for n< 0. The value of x$$\left[ 12 \right]$$ is _____________________.

Consider the sequence
$$x\left[ n \right]$$= $${a^n}u\left[ n \right] + {b^{\partial n}}u\left[ n \right]$$ , where u[n] denotes the unit step sequence and 0<$$\left| a \right| < \left| b \right| < 1.$$
The region of convergence (ROC) of the z-transform of $$\left[ n \right]$$ is

Consider the signal $$x\left[ n \right] = 6\delta \left[ {n + 2} \right] + 3\delta \left[ {n + 1} \right] + 8\delta \left[ n \right] + 7\delta \left[ {n - 1} \right] + 4\delta \left[ {n - 2} \right]$$.

If X$$({e^{t\omega }})$$is the discrete-time Fourier transform of x[n],

then $${1 \over \pi }\int\limits_{ - \pi }^\pi X ({e^{j\omega }}){\sin ^2}(2\omega )d\omega $$ is equal to ____________.

A continuous-time sinusoid of frequency 33 Hz is multiplied with a periodic Dirac impulse train of frequency 46 Hz. The resulting signal is passed through an ideal analog low-pass filter with a cutoff frequency of 23Hz. The fundamental frequency (in Hz) of the output is _____________________.

A continuous -time function $$x\left( t \right)$$ is periodic with period $$T$$. The function is sampled uniformly with a sampling period $${T_s}$$. In which one of the following cases is the sampled signal periodic?

A first-order low-pass filter of time constant T is excited with different input signals (with zero initial conditions up to t = 0). Match the excitation signals X, Y, Z with the corresponding time responses for $$t\, \ge 0$$:
X: Impulse P: 1 $$ - {e^{ - t/T}}$$
Y: Unit step Q: t $$ - T(1 - {e^{ - t/T}})$$
Z: Ramp R: $${e^{ - t/T}}$$

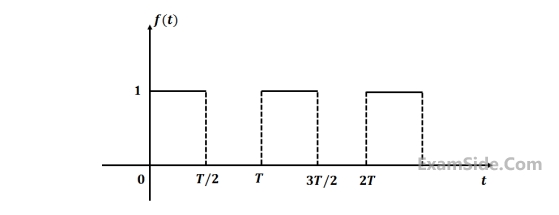
The Laplace transform of the casual periodic square wave of period T shown in the figure below is

Which one of the following is an eight function of the class of all continuous-time, linear, time- invariant systems u(t) denotes the unit-step function?

In a huge pile of apples and oranges, both ripe and unripe mixed together, 15% are unripe fruits. Of the unripe fruits, 45% are apples. Of the ripe ones, 66% are oranges. If the pile contains a total of 5692000 fruits, how many of them are apples?

Michael lives 10 km away from where I live. Ahmed lives 5 km away and Susan lives 7 km away from where I live. Arun is farther away than Ahmed but closer than Susan from where I live. From the information provided here, what is one possible distance (in km) at which I live from Arun's place?