2025
GATE ECE 20252024
GATE ECE 20242023
GATE ECE 20232022
GATE ECE 20222021
GATE ECE 20212019
GATE ECE 20192018
GATE ECE 20182017
GATE ECE 2017 Set 1GATE ECE 2017 Set 22016
GATE ECE 2016 Set 2GATE ECE 2016 Set 1GATE ECE 2016 Set 32015
GATE ECE 2015 Set 2GATE ECE 2015 Set 1GATE ECE 2015 Set 32014
GATE ECE 2014 Set 4GATE ECE 2014 Set 3GATE ECE 2014 Set 2GATE ECE 2014 Set 12013
GATE ECE 20132012
GATE ECE 20122011
GATE ECE 20112010
GATE ECE 20102009
GATE ECE 20092008
GATE ECE 20082007
GATE ECE 20072006
GATE ECE 20062005
GATE ECE 20052004
GATE ECE 20042003
GATE ECE 20032002
GATE ECE 20022001
GATE ECE 20012000
GATE ECE 20001999
GATE ECE 19991998
GATE ECE 19981997
GATE ECE 19971996
GATE ECE 19961995
GATE ECE 19951994
GATE ECE 19941993
GATE ECE 19931992
GATE ECE 19921991
GATE ECE 19911990
GATE ECE 19901989
GATE ECE 19891988
GATE ECE 19881987
GATE ECE 1987GATE ECE 2014 Set 4
Paper was held on Thu, Jan 1, 1970 12:00 AM
1
For a given sample-and-hold circuit, if the value of the hold capacitor is increased, then
2
If the emitter resistance in a common-emitter voltage amplifier is not bypassed, it will
3
Consider the common-collector amplifier in the figure (bias circuitry ensures that the transistor
operates in forward active region, but has been omitted for simplicity). Let IC be the collector
current, VBE be the base-emitter voltage and VT be the thermal voltage. Also, 𝑔m and 𝑟o are the small-signal transconductance and output resistance of the transistor, respectively. Which one of the
following conditions ensures a nearly constant small signal voltage gain for a wide range of values
of RE?
4
A BJT in common-base configuration is used to amplify a signal received by a $$50\,\Omega $$ antena. Assume kT/q = 25 mV. The value of the collector bias current ( in mA ) required to match the input impedance of the amplifier to the impedance of the antena is ______.
5
For the common collector amplifier shown in the figure, the BJT has high $${V_{CE\left( {sat} \right)}},$$ and $${V_{BE}}$$ $$\, = \,\,0.7\,\,\,V$$. The maximum undistorted peak-to-peak output voltage $${V_o}$$ (in Volts) is _____.
6
The circuit shown represents
7
An M - level PSK modulation scheme is used to transmit independent binary digits over a band-pass channel with bandwidth 100 kHz. The bit rate is 200 kbps and the system characteristic is a raised-cosine spectrum with 100% excess bandwidth. The minimum value of M is ___________________________.
8
Consider the Z- channel given in the figure. The input is 0 or 1 with equal probability.
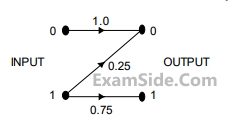
If the output is 0, the probability that the input is also 0 equals____________________________________
If the output is 0, the probability that the input is also 0 equals____________________________________9
If calls arrive at a telephone exchange such that the time of arrival of any call is independent of the time of arrival of earlier or future calls, the probability distribution function of the total number of calls in a fixed time interval will be
10
Consider a discrete-time channel Y = X + Z, where the additive noise Z is signal- dependent. In particular, given the trasmitted symbol $$X\, \in \,\{ \, - \,a,\,\, + \,a\} $$ at any instant, the noise sample Z is chosen independently from a Gaussian distribution with mean $$\beta X$$ and unit variance. Assume a threshold detector with zero threshold at the receiver. When $$\beta $$ = 0 the BER was found to be $$Q\,(a) = 1\, \times \,{10^{ - 8}}$$.
$$\left( {Q\,\,(v)\, = {1 \over {\sqrt {2\,\pi } }}\,\int\limits_v^\infty {{e^{ - {u^2}/2}}} } \right.$$ du, and for v > 1,
use $$Q\,(v) \approx \,{e^{ - {v^2}/2}}$$
When $$\beta = - \,0.3,\,$$ the BER is closed to
use $$Q\,(v) \approx \,{e^{ - {v^2}/2}}$$
When $$\beta = - \,0.3,\,$$ the BER is closed to
11
Consider a communication scheme where the binary valued signal X satisfies P{X = + 1} = 0.75 and P {X = - 1} = 0.25. The received signal Y = X + Z, where Z is a Gaussian random variable with zero mean and variance $${\sigma ^2}$$. The received signal Y is fed to the threshold detector. The output of the threshold detector $${\hat X}$$ is:
$$$\hat X:\left\{ {\matrix{
{ + \,1,} & {Y\, > \tau } \cr
{ - \,1,} & {Y\, \le \,\,\tau .} \cr
} } \right.$$$
To achieve a minimum probability of error $$P\{ \hat X\, \ne \,X\} $$, the threshold $$\tau $$ should be
12
For the second order closed-loop system shown in the figure, the natural frequency (in rad/s)
is
13
Consider a transfer function $$G_p\left(s\right)\;=\;\frac{ps^2+3ps\;-2}{s^2+\left(3+p\right)s\;+\left(2-p\right)}$$ with 'p' a positive real parameter.
The maximum value of 'p' until which Gp remains stable is ________.
14
The characteristic equation of a unity negative feedback system 1 + KG(s) = 0. The open loop
transfer function G(s) has one pole at 0 and two poles at -1. The root locus of the system for
varying K is shown in the figure.
The constant damping ratio line, for $$\xi$$ = 0.5 , intersects the root locus at point A. The distance from the origin to point A is given as 0.5. The value of K at point A is ________ .
15
In a Bode magnitude plot, which one of the following slopes would be exhibited at high
frequencies by a 4th order all-pole system?
16
The state transition matrix $$\phi \left( t \right)$$ of a system $$$\left[ {\matrix{
{\mathop {{x_1}}\limits^ \bullet } \cr
{\mathop {{x_2}}\limits^ \bullet } \cr
} } \right] = \left[ {\matrix{
0 & 1 \cr
0 & 0 \cr
} } \right]\left[ {\matrix{
{{x_1}} \cr
{{x_2}} \cr
} } \right] is$$$
17
In the circuit shown in the figure, if C = 0, the expression for Y is
18
A 16-bit ripple carry adder is realized using 16 identical full adders (FA) as shown in the figure.
The carry-propagation delay of each FA is 12 ns and the sum-propagation delay of each FA is
15 ns. The worst case delay (in ns) of this 16-bit adder will be_______________.
19
An 8-to-1 multiplexer is used to implement a logical function Y as shown in the figure. The output Y is given by
20
The output (Y) of the circuit shown in the figure is
21
For an antenna radiating in free space, the electric field at a distance of 1 km is found to be 12 m V/m. Given that intrinsic impedance of the free space is 120$$\pi \Omega $$, the magnitude of average power density due to this antenna at a ditance of 2 km from the antenna (in n W/$${m^2}$$) is
22
Match column A with column B.
Column
1. Point electromagnetic source
2. Dish antenna
3. Yagi-Uda antenna
Column
P. Highly directional
Q. End fire
R. Isotropic
23
If $$\overrightarrow{\mathrm E}=-\left(2\mathrm y^2\;-3\mathrm{yz}^2\right)\widehat{\mathrm x}\;-\left(6\mathrm{xy}^2-3\mathrm{xz}^2\right)\widehat{\mathrm y}+\left(6\mathrm{xyz}\right)\widehat{\mathrm z}$$
is the electric field in a source free region, a valid expression for the electrostatic potential is
24
The electric field (assumed to be one-dimensional) between two points A and B is shown. Let
$$\psi_A$$ and $$\psi_B$$ be the electrostatic potentials at A and B, respectively. The value of $$\psi_A$$ − $$\psi_B$$ in
Volts is ________.
25
Consider two BJT's biased at the same collector current with area A1 = 0.2 μm × 0.2 μm and
A2 = 300 μm × 300 μm. Assuming that all other device parameters are identical, kT/q = 26
mV, the intrinsic carrier concentration is 1 × 1010 cm-3, and q = 1.6 × 10-19 C, the difference
between the base-emitter voltages (in mV) of the two BJT's (i.e., VBE1 – VBE2) is___________.
26
In the figure ln(ρi) is plotted as a function of 1/T, where ρi
the intrinsic resistivity of silicon,
T is is the temperature, and the plot is almost linear.
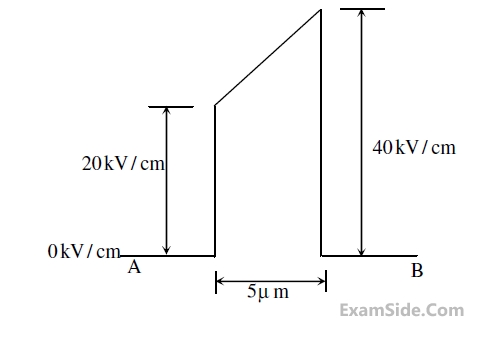
The slope of the line can be used to estimate
27
The cut-off wavelength (in µm) of light that can be used for intrinsic excitation of a
semiconductor material of bandgap Eg= 1.1 eV is ________.
28
Consider a silicon sample doped with ND = 1×1015/cm3 donor atoms. Assume that the
intrinsic carrier concentration ni = 1.5×1010/cm3. If the sample is additionally doped with NA = 1×1018/cm3 acceptor atoms, the approximate number of electrons/cm3 in the sample, at
T=300 K, will be _________________.
29
An N-type semiconductor having uniform doping is biased as shown in the figure.
If EC is the lowest energy level of the conduction band, EV is the highest energy level of the valance band and EF is the Fermi level, which one of the following represents the energy band diagram for the biased N-type semiconductor?
30
The series $$\sum\limits_{n = 0}^\infty {{1 \over {n!}}\,} $$ converges to
31
For a right angled triangle, if the sum of the lengths of the hypotenuse and a side is kept constant, in order to have maximum area of the triangle, the angle between the hypotenuse and the side is
32
The magnitude of the gradient for the function $$f\left( {x,y,z} \right) = {x^2} + 3{y^2} + {z^3}\,\,$$ at the point $$(1,1,1)$$ is _________.
33
The directional derivative of $$f\left( {x,y} \right) = {{xy} \over {\sqrt 2 }}\left( {x + y} \right)$$ at $$(1, 1)$$ in the direction of the unit vector at an angle of $${\pi \over 4}$$ with $$y-$$axis, is given by ________.
34
Given $$\,\,\overrightarrow F = z\widehat a{}_x + x\widehat a{}_y + y\widehat a{}_z.\,\,$$ If $$S$$ represents the portion of the sphere $${x^2} + {y^2} + {z^2} = 1$$ for $$\,z \ge 0,$$ then $$\int\limits_s {\left( {\nabla \times \overrightarrow F .} \right)\overrightarrow {ds} \,\,} $$ is ________.
35
If calls arrive at a telephone exchange such that the time of arrival of any call is independent of the time of arrival of earlier of future calls, the probability distribution function of the total number of calls in a fixed time interval will be
36
Parcels from sender $$S$$ to receiver $$R$$ pass sequentially through two post - offices. Each post - office has a probability $${1 \over 5}$$ of losing an incoming parcel, independently of all other parcels. Given that a parcel is lost, the probability that it was lost by the second post - office is _________.
37
Let $$X$$ be a zero mean unit variance Gaussian random variable. $$E\left[ {\left| X \right|} \right]$$ is equal to ______
38
With initial values $$\,\,\,y\left( 0 \right) = y'\left( 0 \right) = 1,\,\,\,$$ the solution of the differential equation $$\,\,{{{d^2}y} \over {d{x^2}}} - 4{{dy} \over {dx}} + 4y = 0\,\,$$ at $$x=1$$ is ________.
39
If $$a$$ and $$b$$ are constants, the most general solution of the differential equation $$\,{{{d^2}x} \over {d{t^2}}} + 2{{dx} \over {dt}} + x = 0$$ is
40
The unilateral Laplace transform of $$f(t)$$ is $${1 \over {{s^2} + s + 1}}$$. Which one of the following is the unilateral Laplace transform of $$g\left( t \right) = t.f\left( t \right)?$$
41
An 8085 microprocessor executes “STA 1234H” with starting address location 1FFEH (STA copies the contents of the
Accumulator to the 16-bit address location). While the instruction is fetched and executed, the sequence of values written
at the address pins $${A_{15}}$$ − $${A_{8}}$$ is
42
The steady state output of the circuit shown in the figure is given by
$$$y\left( t \right) = {\rm A}\left( \omega \right)\sin \left( {\omega t + \phi \left( \omega \right)} \right)$$$
If the amplitude $$\left| {{\rm A}\left( \omega \right)} \right| = 0.25$$, then the frequency $$\omega $$ is
43
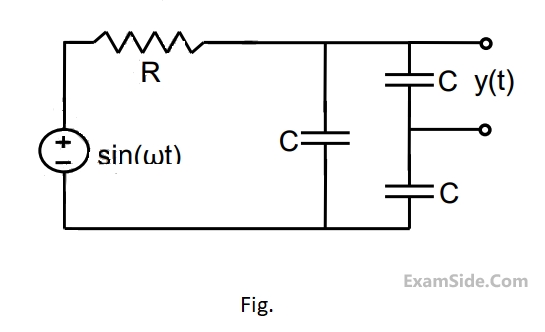
The equivalent resistance in the infinite ladder network shown in the figure, is$${R_e}$$
The value of $${R_e}/R$$ is _______________
44
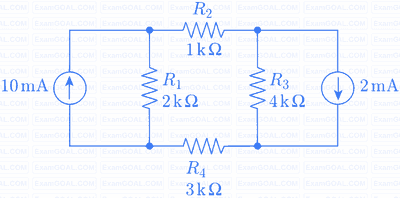
The magnitude of current (in mA) through the resistor R2 in the figure shown is _____.
45
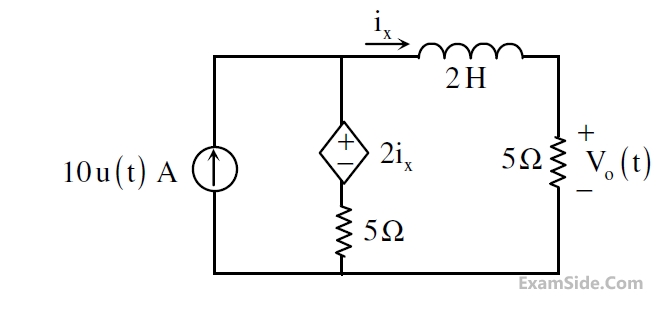
In the circuit shown in the figure, the value of V0(t) (in Volts) for $$t\rightarrow\infty$$ is ______.
46
For the two-port network shown in the figure, the impedance (Z) matrix (in Ω) is
47
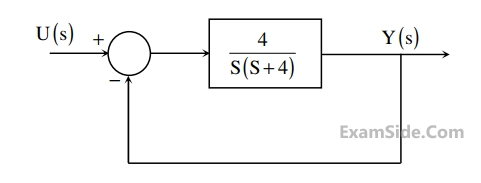
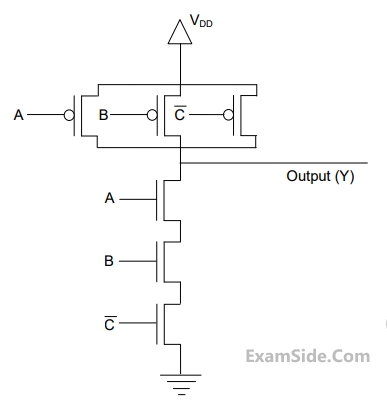
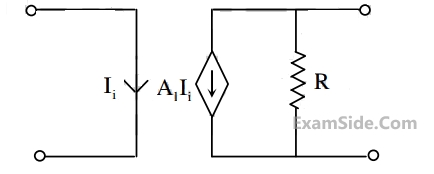
The circuit shown in the figure represents a
48
The unilateral Laplace transform of F(t) is $${1 \over {{s^2} + s + 1}}$$. Which one of the following is the unilateral Laplace transform of g(t) = $$t \cdot f\left( t \right)$$
49
A stable linear time invariant (LTI) system has a transfer function H(s) = $${1 \over {{s^2} + s - 6}}$$. To make this system casual it needs to be cascaded with another LTI system having a transfer function H1(s). A correct choice for H1(s) among the following options is
50
A casual LTI system has zero initial conditions and impulse response h(t). Its input x(t) and output y(t) are related through the linear constant - coefficient differential equation
$$${{{d^2}y\left( t \right)} \over {d{t^2}}} + \alpha {{dy\left( t \right)} \over {dt}} + {\alpha ^2}y\left( t \right) = x\left( t \right).$$$
Let another signal g(t) be defined as $$\left( t \right) = {\alpha ^2}\int_0^t {h\left( \tau \right)d\tau + {{dh\left( t \right)} \over {dt}} + \alpha h\left( t \right)} $$.
If G(s) is the Laplace transform of g(t), then the number of poles of G(s) is ______.
51
The N-point DFT X of a sequence x[n] 0 ≤ n ≤ N − 1 is given by
$$X\left[ k \right] = {1 \over {\sqrt N }}\,\,\sum\limits_{n = 0}^{N - 1} x \,[n\,]e{\,^{ - j{{2\pi } \over N}nk}}$$, 0$$ \le k \le N - 1$$
Denote this relation as X = DFT(x). For N= 4 which one of the following sequences satisfies DFT (DFT(x) ) = ___________.
$$X\left[ k \right] = {1 \over {\sqrt N }}\,\,\sum\limits_{n = 0}^{N - 1} x \,[n\,]e{\,^{ - j{{2\pi } \over N}nk}}$$, 0$$ \le k \le N - 1$$
Denote this relation as X = DFT(x). For N= 4 which one of the following sequences satisfies DFT (DFT(x) ) = ___________.
52
The sequence x $$\left[ n \right]$$ = $${0.5^n}$$ u[n], where u$$\left[ n \right]$$ is the unit step sequence, is convolved with itself to obtain y $$\left[ n \right]$$ . Then $$\sum\limits_{n = \infty }^{ + \infty } y \left[ n \right]$$ is ____________.
53
A real - values signal x(t) limited to the frequency band $$\left| f \right| \le {W \over 2}$$ is passed through a linear time invariant system whose frequency response is
$$H(f) = \left\{ {\matrix{ {{e^{ - j4\pi f}},} & {\left| f \right| \le \,{W \over 2}} \cr {0,} & {\left| f \right| > \,{W \over 2}} \cr } } \right.$$
$$H(f) = \left\{ {\matrix{ {{e^{ - j4\pi f}},} & {\left| f \right| \le \,{W \over 2}} \cr {0,} & {\left| f \right| > \,{W \over 2}} \cr } } \right.$$
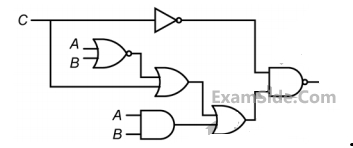
The output of the system is
54
A Fourier transform pair is given by $${\left( {{2 \over 3}} \right)^n}$$ u $$\left[ {n + 3} \right]\,\mathop \Leftrightarrow \limits^{FT} \,{{A{e^{ - j6\pi f}}} \over {1 - \left( {{2 \over 3}} \right){e^{ - j2\pi f}}}}$$ ,
where u(n) donotes the unit step sequence. The values of A is_______________.
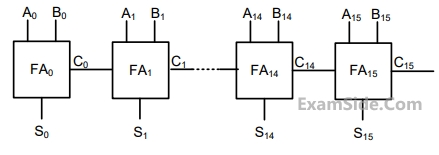
where u(n) donotes the unit step sequence. The values of A is_______________.