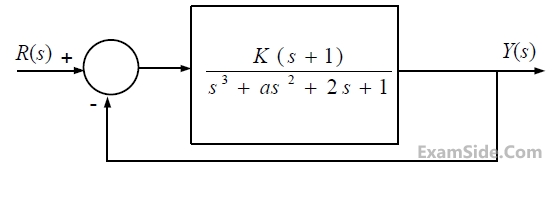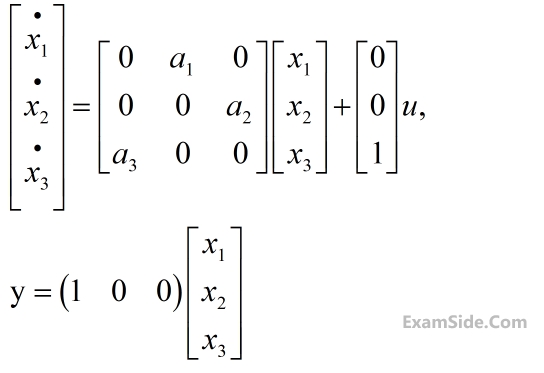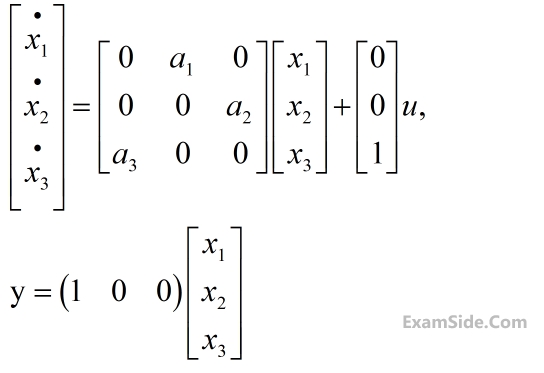1
The diodes and capacitors in the circuit shown are ideal. The voltage v(t)
across the diode D1 is

2
The current i
b through the base of a silicon npn transistor is
$$1\;+\;0.1\;\cos\left(10000\;\mathrm\pi\;\mathrm t\right)$$ mA
. At 300 K,
the $$r_\mathrm\pi$$ in the small signal model of the transistor is

3
The voltage gain A
v of the circuit shown below is

5
A source alphabet consists of N symbols with the probability of the first two symbols being the same. A source encoder increases the probability of the first symbol by a small amount $$\varepsilon $$ and decreases that of the second by $$\varepsilon $$. After encoding, the entropy of the source
6
In a base band communications link, frequencies up to 3500 Hz are used for signaling. Using a raised cosine pulse with 75% excess bandwidth and for no inter-symbol interference, the maximum possible signaling rate in symbols per second is
7
Two independent random variable X and Y are uniformly distributed in the interval [ - 1, 1]. The probability that max [X, Y] is less than 1/2 is
8
The power spectral density of a real process X(t) for positive frequencies is shown below. The value of $$E\,\left[ {{X^2}\,(t)} \right]$$ and $$E\,\left[ {X\,(t)} \right]$$, respectively, are

9
A BPSK scheme operating over an AWGN channel with noise power spectral density of N
02, uses equi-probable signals
$$${s_1}\left( t \right) = \sqrt {{{2E} \over T}\,\sin \left( {{\omega _c}t} \right)} $$$
and
$$${s_2}\left( t \right) = - \sqrt {{{2E} \over T}\,\sin \left( {{\omega _c}t} \right)} $$$
over the symbol interval, $$(0, T)$$. If the local oscillator in a coherent receiver is ahead in phase by 450 with respect to the received signal, the probability of error in the resulting system is
10
A binary symmetric channel (BSC) has a transition probability of 1/8. If the binary transmit symbol X is such that P(X =0) = 9/10, then the probability of error for an optimum receiver will be
11
The signal m(t) as shown is applied both to a phase modulator (with
k
p
as the phase constant) and
a frequency modulator (with
k
f
as the frequency constant) having the same carrier frequency.

The ratio kp/kf
(in rad/Hz) for the same maximum phase deviation is
12
The feedback system shown below oscillates at 2 rad/s when
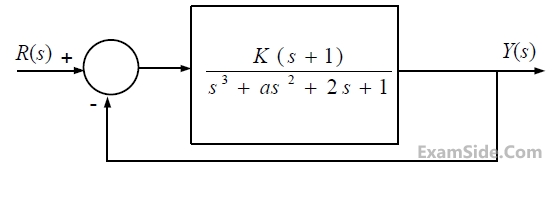
13
A system with transfer function
g(s) = $${{\left( {{s^2} + 9} \right)\left( {s + 2} \right)} \over {\left( {s + 1} \right)\left( {s + 3} \right)\left( {s + 4} \right)}},$$ is excited by $$\sin \left( {\omega t} \right).$$ The steady-state output of the system is zero at
14
The transfer function of a compensator is given as $${G_C}(s) = {{s + a} \over {s + b}}.$$
$${G_C}(s)$$ is a lead compensator if
15
The transfer function of a compensator is given as $${G_C}(s) = {{s + a} \over {s + b}}.$$
The phase of the above lead compensator is maximum at
16
The state variable description of an LTI system is given by
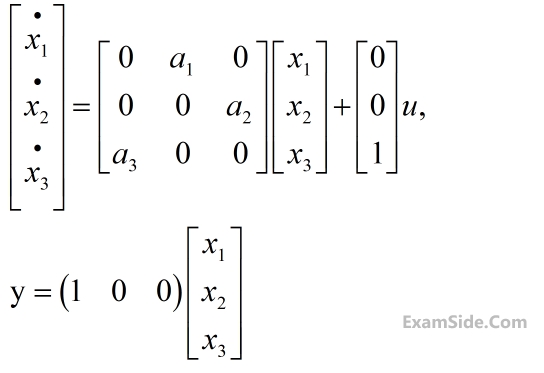
where y is the output and u is input. The system is controllable for
17
The state transition diagram for the logic circuit shown is

18
The output Y of a 2-bit comparator is logic 1 whenever the 2-bit input A is greater than the 2-bit input B.
The number of combinations for which the output is logic 1, is
19
Consider the given circuit. In this circuit, the race around

20
The magnetic field along the propagation direction inside a rectangular waveguide with the cross section shown in the figure is $${H_Z} = 3\,\,\cos \,\,(2.094\,\, \times \,\,{10^2}x)\,\,\,\cos \,(2.618\,\, \times \,\,{10^2}y)$$
$$\cos \,\,(6.283\,\, \times \,\,{10^{10}}t\, - \beta \,z)$$
The phase velocity $${V_p}$$ of the wave inside the waveguide satisfies

21
The electric field of a uniform plane electromagnetic wave in free spce, along the positive x direction, is given by $$\vec E = 10\left( {{{\widehat a}_y} + j{{\widehat a}_z}} \right){e^{ - j25x}}.$$ The frequency and polarization of the wave respectively are
22
A coaxial cable with an inner diameter of 1 mm and outer diameter of 2.4 mm is filled with a dielectric of relative permittivity 10.89. Given $${\mu _0} = \,4\,\pi \, \times \,{10^{ - 7}}$$
$$H/m,\,\,{\varepsilon _0} = {{{{10}^{ - 9}}\,} \over {36\,\pi }}\,F/m,$$ the characteristic impedance of the cable is
23
A plane wave propagating in air with $$\vec E = \left( {8{{\widehat a}_x} + 6{{\widehat a}_y} + 5{{\widehat a}_z}} \right){\mkern 1mu} {\mkern 1mu} {e^{j\left( {\omega t + 3x - 4y} \right)}}{\mkern 1mu} {\mkern 1mu} V/m$$ is incident on a perfectly conducting slab positioned at $$x \le 0$$. The $$\overrightarrow E $$ field of the reflected wave is
24
A transmission line with a characteristic impedance of 100 $$\Omega $$ is used to match a 50 $$\Omega $$ section to a 200 $$\Omega $$ section. If the matching is to be done both at 429 MHz and 1 GHz, the tength of the transmission line can be approximately
25
The radiation pattern of an antenna in spherical co-ordinates is given by
$$$F\,(\theta )\, = {\cos ^4}\,\theta \,\,\,;\,\,0\,\, \le \,\,\theta \,\, \le \,\,\pi /2$$$
The directivity of the antenna is
26
An infinitely long uniform solid wire of radius a carries a uniform dc current of density $$\widehat{\mathrm j}$$
The magnetic field at a distance r from the center of the wire is proportional to
27
An infinitely long uniform solid wire of radius a carries a uniform dc current of density $$\widehat{\mathrm j}$$.
A hole of radius b (b < a) is now drilled along the length of the wire at a distance d from the center
of the wire as shown below.

The magnetic field inside the hole is
29
The source of a silicon (ni = 1010 per cm3) n - channel MOS transistor has an aewa of 1 sq $$\mu m$$ and a depth of 1 $$\mu m$$ . If the dopant density in the source is 1019/cm3, the number of holes in the source region with the above volume is approximately
30
In the three dimensional view of a silicon n-channel
MOS transistor shown below, $$\delta = 20$$ nm. The transistor is of width 1 $$\mu m$$. The depletion width formed at every p-n junction is 10 nm. The relative permittivities of Si and SiO
2, respectively, are 11.7 and 3.9, and $${\varepsilon _0}$$ = 8.9 $$ \times {10^{ - 12}}$$ F/m.

The source-body junction capacitance is approximately
31
In the three dimensional view of a silicon n-channel
MOS transistor shown below, $$\delta = 20$$ nm. The transistor is of width 1 $$\mu m$$. The depletion width formed at every p-n junction is 10 nm. The relative permittivities of Si and SiO
2, respectively, are 11.7 and 3.9, and $${\varepsilon _0}$$ = 8.9 $$ \times {10^{ - 12}}$$ F/m.

The gate-source overlap capacitance is approximately
32
In the
CMOS circuit shown, electron and hole mobilities are equal, and M
1 and M
2 are equally sized. The device M
1 is in the linear region if

33
Given that $$A = \left[ {\matrix{
{ - 5} & { - 3} \cr
2 & 0 \cr
} } \right]$$ and $${\rm I} = \left[ {\matrix{
1 & 0 \cr
0 & 1 \cr
} } \right],$$ the value of $${A^3}$$ is
34
The direction of vector $$A$$ is radially outward
from the origin, with $$\left| A \right| = K\,{r^n}$$
where $${r^2} = {x^2} + {y^2} + {z^2}$$ and $$K$$ is constant.
The value of $$n$$ for which $$\nabla .A = 0\,\,$$ is
35
Two independent random variables $$X$$ and $$Y$$ are uniformly distributed in the interval $$\left[ { - 1,1} \right].$$ The probability that max $$\left[ {X,Y} \right]$$ is less than $$1/2$$ is
36
A fair coin is tossed till a head appears for the first time. The probability that the number of required tosses is odd, is
37
With initial condition $$x\left( 1 \right)\,\,\, = \,\,\,\,0.5,\,\,\,$$ the solution of the differential equation, $$\,\,\,t{{dx} \over {dt}} + x = t\,\,\,$$ is
38
If $$x\left[ N \right] = {\left( {1/3} \right)^{\left| n \right|}} - {\left( {1/2} \right)^n}\,u\left[ n \right],$$ then the region of convergence $$(ROC)$$ of its $$Z$$-transform in the $$Z$$-plane will be
39
The unilateral Laplace transform of $$f(t)$$ is
$$\,{1 \over {{s^2} + s + 1}}.$$ The unilateral Laplace transform of $$t$$ $$f(t)$$ is
40
Consider the differential equation
$${{{d^2}y\left( t \right)} \over {d{t^2}}} + 2{{dy\left( t \right)} \over {dt}} + y\left( t \right) = \delta \left( t \right)$$
with $$y\left( t \right)\left| {_{t = 0} = - 2} \right.$$ and $${{dy} \over {dt}}\left| {_{t = 0}} \right. = 0.$$
The numerical value of $${{dy} \over {dt}}\left| {_{t = 0}.} \right.$$ is
41
If $$x = \sqrt { - 1} ,\,\,$$ then the value of $${X^x}$$ is
42
Given $$f\left( z \right) = {1 \over {z + 1}} - {2 \over {z + 3}}.$$ If $$C$$ is a counterclockwise path in the $$z$$-plane such that
$$\left| {z + 1} \right| = 1,$$ the value of $${1 \over {2\,\pi \,j}}\oint\limits_c {f\left( z \right)dz} $$ is
43
The impedance looking into nodes 1 and 2 in the given circuit is

44
In the circuit shown below, current through the inductor is

45
If VA - VB = 6 V then VC - VD is

46
Assuming both the voltage sources are in phase the value of R for which maximum power is
transferred from circuit A to circuit B is

47
With 10 V dc connected at port A in the linear nonreciprocal two-port network shown below, the
following were observed:
(i) 1Ω connected at port B draws a current of 3 A
(ii) 2.5Ω connected at port B draws a current of 2 A

For the same network, with 6 V dc connected at port A, 1Ω connected at port B draws 7/3 A. If
8 V dc is connected to port A, the open circuit voltage at port B is
48
With 10 V dc connected at port A in the linear nonreciprocal two-port network shown below, the
following were observed:
(i) 1Ω connected at port B draws a current of 3 A
(ii) 2.5Ω connected at port B draws a current of 2 A

With 10 V dc connected at port A, the current drawn by 7Ω connected at port B is
49
In the following figure, C
1 and C
2 are ideal capacitors. C
1 has been charged to 12 V before the
ideal switch S is closed at t = 0. The current i(t) for all t is.
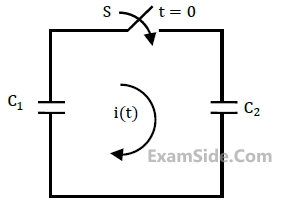
50
The average power delivered to an impedance $(4-j 3) \Omega$ by a current $5 \cos (100 \pi t+100) A$ is
51
If $$x\left[ n \right]$$= $${(1/3)^{\left| n \right|}} - {(1/2)^n}u\left[ n \right]$$, then the region of convergence (ROC) of its Z- transform in the Z-plane will be
52
The input x(t) and output y(t) of a system are related as y(t) = $$\int\limits_{ - \infty }^t x (\tau )\cos (3\tau )d\tau $$.
The system is
53
The Fourier transform of a signal h(t) is $$H(j\omega )$$ =(2 cos $$\omega $$) (sin 2$$\omega $$) / $$\omega $$. The value of h(0) is
54
Let $$y\left[ n \right]$$ denote the convolution of $$h\left[ n \right]$$ and $$g\left[ n \right]$$, where $$h\left[ n \right]$$ $$ = \,{\left( {1/2} \right)^2}\,\,u\left[ n \right]$$ and $$g\left[ n \right]\,$$ is a causal sequence. If $$y\left[ 0 \right]\,$$ $$ = \,1$$ and $$y\left[ 1 \right]\,$$ $$ = \,1/2,$$ then $$g\left[ 1 \right]$$ equals