1
The circuit below implements a filter between the input current i
i and the output voltage v
0. Assume that the op-amp- is ideal, The filter implemented is a

2
In the circuit shown below, assume that the voltage drop across a forward biased
diode is 0.7V. The thermal voltage V
t = kT/q = 25mV. The small signal input
v
i = V
P cos ($$\omega t$$) where V
P = 100mV.

The bias current I
DC through the diodes is
3
In the circuit shown below, assume that the voltage drop across a forward biased
diode is 0.7V. The thermal voltage V
t = kT/q = 25mV. The small signal input
v
i = V
P cos ($$\omega t$$) where V
P = 100mV.

The ac output voltage v
ac is
4
In the circuit shown below, capacitors C
1 and C
2 are very large and are shorts at
the input frequency. V
i
is a small signal input. The gain magnitude $$\left|\frac{{\mathrm V}_0}{{\mathrm V}_\mathrm i}\right|$$
at 10 Mrad/s is

5
For a BJT, the common-base current gain $$\alpha = \,\,0.98$$ and the colector base junction reverse bias saturation current Ico = 0.6 $$\mu {\rm A}$$. This BJT is connected in the common emitter mode and operated in the active region with a base drive current IB = 20$$\mu {\rm A}$$. The collector current Ic for this mode of operation is
6
For the BJT Q
1 in the circuit shown below, $$\beta = \infty ,\,\,\,\,{V_{BEon\,}}\, = \,0.7V,\,\,\,{V_{CEsat}}\, = \,0.7V.$$. The switch is initially closed. at time t = 0, the switch is opened. The time t at which q
1 leaves the active region is

7
A four phase and an eight-phase signal constellation are shown in the figure below.
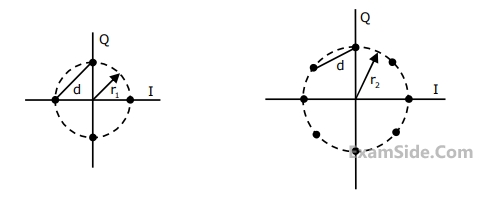
Assuming high SNR and that all signals are equally probable, the additional average transmitted signal energy required by the 8-PSK signal to achieve the same error probability as the 4-PSK signal is
8
X(t) is a stationary random process with autocorrelation function R
x$$\left( \tau \right)$$= exp$$\left( { - \pi {\tau ^2}} \right)$$. This process is passed through the system shown below. The power spectral density of the output process Y(t) is

9
An analog signal is band-limited to 4kHz. sampled at the Nyquist rate and the samples are quantized into 4 levels. The quantized levels are assumed to be independent and equally probable, bit rate is
10
A four phase and an eight-phase signal constellation are shown in the figure below.

For the constraint that the minimum distance between pairs of signal points be d
for both constellations, the radii r1, and r2 of the circles are
11
The root locus plot for a system is given below. The open loop transfer function
corresponding to this plot is given by

12
The differential equation
$$$100\frac{\mathrm d^2\mathrm y}{\mathrm{dt}^2}-20\frac{\mathrm{dy}}{\mathrm{dt}}+\mathrm y=\mathrm x\left(\mathrm t\right)$$$ describes a system with an
input x(t) and an output y(t). The system, which is initially relaxed, is excited by
a unit step input. The output y(t) can be represented by the waveform
13
For the transfer function G$$\left( {j\omega } \right) = 5 + j\omega ,$$ the corresponding Nyquist plot for
positive frequency has the form
14
The input-output transfer function of a plant is h(s)=$${{100} \over {s{{\left( {s + 10} \right)}^2}}}$$. The plant is placed in a unity negative feedback configuration as shown in the figure below.

The gain margin of the system under closed loop unity negative feedback is
15
The input-output transfer function of a plant is h(s)=$${{100} \over {s{{\left( {s + 10} \right)}^2}}}$$. The plant is placed in a unity negative feedback configuration as shown in the figure below.

The signal flow graph that DOES NOT model the plant transfer function H(s) is
16
The block diagram of a system with one input u and two outputs y
1 and y
2 is given below
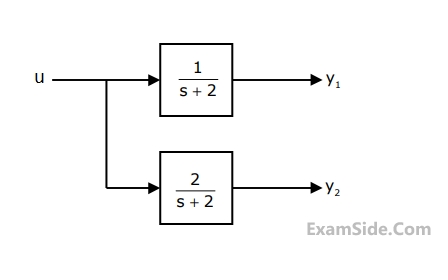
A state space model of the above system in terms of the state vector $$\underline x $$ and the output vector $$\underline y = {\left[ {\matrix{
{{y_1}} & {{y_2}} \cr
} } \right]^\tau }$$ is
17
The logic function implemented by the circuit below is (ground implies a logic "0"

18
When the output Y in the circuit below is ‘1’, it implies that data has

19
Two D flip-flops are connected as a synchronous counter that goes through the following QB QA sequence $$00 \to 11 \to 01 \to 10 \to 00 \to ......$$
20
The output of a 3-stage Johnson (twisted-ring) counter is fed to a digital-to-analog (D/A) converter as shown in the figure below. Assume all the states of the counter to be unset initially. The waveform which represents the D/A converter output V
o is

21
The output Y in the circuit below is always ‘1’ when

22
A transmission line of characteristic impedance 50 $$\Omega $$ is terminated by a 50 $$\Omega $$ load. When excited by a sinusoidal voltage source at 10 GHz, the phase difference between two points spaced 2 mm apart on the line is found to be $$\pi /4$$ radians. The phase velocity of the wave along the line is
23
A transmission line of characteristic impedance 50 $$\Omega $$ is terminated in a load impedance $$Z_L$$. The VSWR of the line is measured as 5 and the first of the voltage naxima in the line is observed at a distance of $$\lambda /4$$ from the load. The value of $$Z_L$$ is
24
The electric and magnetic fields for a TEM wave of frequency $$14 GHz$$ in a homogeneous medium of relative permittivity $${\varepsilon _r}$$ and relative permeability $${\mu _r} = 1$$ are given by
$$$\overrightarrow E = {E_p}\,\,{e^{j\left( {\omega t - 280\pi y} \right)}}\,\,{\widehat u_z}\,\,V/m$$$
$$$\overrightarrow H = \,\,3\,\,{e^{j\left( {\omega \,t - 280\,\,\pi \,y} \right)}}\,\,\widehat u{\,_x}\,\,A/m$$$
Assuming the speed of light in free space to be $$3\,\, \times {10^8}\,\,\,m/s,$$ the intrinsic impedance of free space to be $$120\,\,\,\pi $$, the relative permittivity $${\varepsilon _r}$$ of the medium and the electric field amplitude $${E_p}$$ are
25
The modes in a rectangular waveguide are denoted by $$T{E_{mn}}\,$$/$$T{M_{mn}}\,$$ where m and n are the eigen numbers along the larger and smaller dimensions of the waveguide respectively. Which one of the following satements is TRUE?
26
Consider a closed surface S surrounding volume V. If $$\overrightarrow{\mathrm r}$$
is the position vector of a
point inside S, with $$\widehat n$$ the unit normal on S, the value of the integral is

27
Drift current in the semiconductors depends upon
28
For a BJT the common base current gain $$\alpha$$ = 0.98 and the collector base junction
reverse bias saturation current ICO = 0.6μA. This BJT is connected in the common
emitter mode and operated in the active region with a base drive current
IB=20μA. The collector current IC for this mode of operation is
29
The channel resistance of an N-channel JFET shown in the figure below is 600 W
when the full channel thickness (t
ch) of 10 μm is available for conduction. The
built-in voltage of the gate P
+N junction (V
bi) is -1 V. When the gate to source
voltage (V
GS) is 0 V, the channel is depleted by 1 μm on each side due to the built in
voltage and hence the thickness available for conduction is only 8 μm

The channel resistance when V
GS = -3 V is
30
The channel resistance of an N-channel JFET shown in the figure below is 600 W
when the full channel thickness (t
ch) of 10 μm is available for conduction. The
built-in voltage of the gate P
+N junction (V
bi) is -1 V. When the gate to source
voltage (V
GS) is 0 V, the channel is depleted by 1 μm on each side due to the built in
voltage and hence the thickness available for conduction is only 8 μm

The channel resistance when V
GS = 0 V is
31
In the circuit shown below, for the MOS transistors, $$\mu_nC_{ox}\;=\;100\;\mu A/V^2$$ and the
threshold voltage V
T = 1 V. The voltage V
x at the source of the upper transistor is

32
The system of equations $$x+y+z=6,$$ $$x+4y+6z=20,$$ $$x + 4y + \lambda z = \mu $$ has no solution for values of $$\lambda $$ and $$\mu $$ given by
33
Consider a closed surface $$'S'$$ surrounding a volume $$V.$$ If $$\overrightarrow r $$ is the position vector of a point inside $$S$$ with $$\overrightarrow n $$ the unit normal on $$'S',$$ the value of the integral

is
34
A fair dice is tossed two times. The probability that the $$2$$nd toss results in a value that is higher than the first toss is
35
The solution of differential equation $${{dy} \over {dx}} = ky,y\left( 0 \right) = C$$ is
36
A numerical solution of the equation $$f\left( x \right) = x + \sqrt x - 3 = 0$$ can be obtained using Newton $$-$$ Raphson method. If the starting values is $$x=2$$ for the iteration then the value of $$x$$ that is to be used in the next step is
37
The value of the integral $$\oint\limits_c {{{ - 3z + 4} \over {{z^2} + 4z + 5}}} \,\,dz,$$ when $$C$$ is the circle $$|z| = 1$$ is given by
38
An 8085 assembly language program is given below. Assume that the carry flag is initially unset. The content of the accumulator after the execution of the program is
MVI A,07H
RLC
MOV B,A
RLC
RLC
ADD B
RRC
39
In the circuit shown below, the Norton equivalent current in amperes with respect to terminals
P and Q is

40
In the circuit shown below the value of R
L such that the power transferred to R
L is maximum

41
If the unit step response of a network is $$(1-e^{-\alpha t})$$, then its unit impulse response
is
42
In the circuit shown below, the initial charge on the capacitor is 2.5 mC, with the
voltage polarity as indicated. The switch is closed at time t=0. The current i(t) at
a time t after the switch is closed is
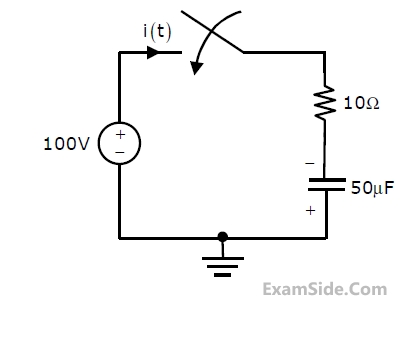
43
In the circuit shown below, the network N is described by the following Y matrix:
$$$Y\;=\;\begin{bmatrix}0.1S&-0.01S\\0.01S&0.1S\end{bmatrix}$$$
The voltage gain $$\frac{V_2}{V_1}$$ is

44
In the circuit shown below, the current I is equal to

45
If $$F\left( s \right) = L\left[ {f\left( t \right)} \right] = {{2\left( {s + 1} \right)} \over {{s^2} + 4s + 7}}$$ then the initial and final values of f(t) are respectively
46
The first six points of the 8-point DFT of a real valued sequence are 5, 1 - j3, 0, 3- j4, 0 and 3+ j4. The last two points of the DFT are respectively
47
The differential equation $$100{{{d^2}y} \over {dt}} - 20{{dy} \over {dt}} + y = x\left( t \right)$$ describes a system with an input x(t) and output y(t). The system, which is initially relaxed, is excited by a unit step input. The output y(t) can be represented by the waveform
48
An input x(t) = exp( -2t) u(t) + $$\delta $$(t-6) is applied to an LTI system with impulse response h(t) = u(t). The output is
49
A system is defined by its impulse response $$h\left( n \right) = {2^n}\,u\left( {n - 2} \right).$$ The system is
50
Two system $${H_1}\left( z \right)$$ and $${H_2}\left( z \right)$$ are connected in cascade as shown below. The overall output $$y\left( n \right)$$ is the same as the input $$x\left( n \right)$$ with a one unit delay. The transfer function of the second system $${H_2}\left( z \right)$$ is
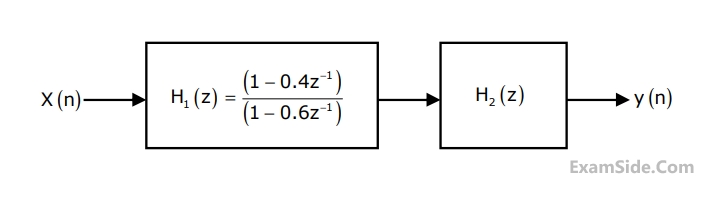

 The bias current IDC through the diodes is
The bias current IDC through the diodes is The ac output voltage vac is
The ac output voltage vac is





 The gain margin of the system under closed loop unity negative feedback is
The gain margin of the system under closed loop unity negative feedback is The signal flow graph that DOES NOT model the plant transfer function H(s) is
The signal flow graph that DOES NOT model the plant transfer function H(s) is






 The channel resistance when VGS = -3 V is
The channel resistance when VGS = -3 V is The channel resistance when VGS = 0 V is
The channel resistance when VGS = 0 V is
 is
is 







 The gain margin of the system under closed loop unity negative feedback is
The gain margin of the system under closed loop unity negative feedback is The signal flow graph that DOES NOT model the plant transfer function H(s) is
The signal flow graph that DOES NOT model the plant transfer function H(s) is











