1
Three identical RC-Coupled transistor amplifiers are cascaded. If each of the
amplifiers has a frequency response as shown in figure, the overall frequency
response is as given as
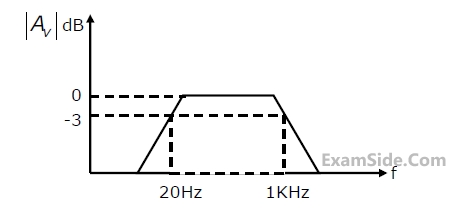
2
Consider the following statements in connection with the CMOS inverter in the Figure.
Where both the MOSFETS are of enhancement type and both have a threshold voltage of 2V.
Statement 1: T1 conducts when Vi $$ \ge \,2\,V$$.
Statement 2: T1 is always in saturation when $${V_0}\, = \,0\,V$$.
Which of the following is correct?

3
The circuit in the figure employs positive Feedback and is intended to generate sinusoidal oscillation. If at a frequency f$$_0$$, B(f)= $${{\Delta {V_f}(f)} \over {{V_0}(f)}} = {1 \over 6}\,\,\angle {0^0}$$ then to sustain oscillation at this frequency.
4
In a negative feedback amplifier using voltage - Series (i.e., voltage - sampling, series mixing) feedback
5
If the variance $$\sigma _d^2$$ of d(n) = x(n - 1) is one-tenth the variance $$\sigma _x^2$$ of a stationary zero-mean discrete-time signal x(n), then the normalized autocorrelation function $${R_{xx}}\,(k)\,/\,\,\sigma _x^2\,at\,\,k\,\, = \,1$$ is
6
For a bit-rate of 8 kbps, the best possible values of the transmitted frequencies in a coherent binary FSK system are
7
A 1 MHz sinusoidal carrier is amplitude modulated by a symmetrical square wave
of period 100 µsec. Which of the following frequencies will NOT be present in the
modulated signal?
8
The transfer function of a system is $$G\left(s\right)\;=\;\frac{100}{\left(s\;+\;1\right)\left(s\;+\;100\right)}$$.For a unit step input
to the system the approximate settling time for 2% criterion is
9
The system shown in Figure remains stable when

10
The characteristic polynomial of a system is
q(s) = 2s5 + s4 + 4s3 + 2s2 + 2s + 1.
The system is
11
Which of the following points is NOT on the root locus of a system with the open
loop transfer function
$$$G\left(s\right)H\left(s\right)=\frac K{s(s+1)(s+3)}$$$
12
Consider a system with the transfer function
$$$G\left(s\right)=\frac{s+6}{Ks^2+s+6}$$$
Its damping ratio
will be 0.5 when the value of K is
13
The phase margin of a system with the open-loop transfer function
G(s)H(s)=$${{(1 - s)} \over {(1 + s)(2 + s)}}$$ is?
14
The system with the open loop transfer function G(s)H(s)=$${1 \over {s\left( {{s^2} + s + 1} \right)}},$$ has a gain margin of
15
The Nyquist plot of an all-pole second order open-loop system is shown in Figure.
Obtain the transfer function of the system.
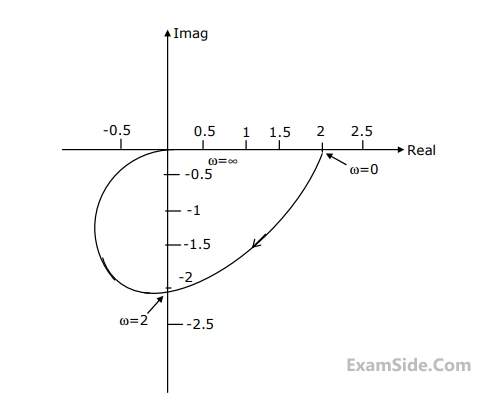
16
A unity feedback system has the plant transfer function
Gp(s)=$${1 \over {\left( {s + 1} \right)\left( {2s + 1} \right)}}$$
(a) Determine the frequency at which the plant has a phase lah of 90o.
(b) An intergral controller with transfer function Gc(s)=$${k \over s}$$ , isplaced in the forwardpath the value of k such that the compensated system has an open loop gain margin of 2.5.
(c) Determine the steady state errors of the compensated system to unit-step and unit-ramp inputs.
17
The transfer function Y(s)/U(s) of a system described by the state equations
$$\mathop x\limits^ \bullet $$(t) = -2x(t)+2u(t)
y(t) = 0.5x(t) is
18
The block diagram of a linear time invariant system is given in Figure is
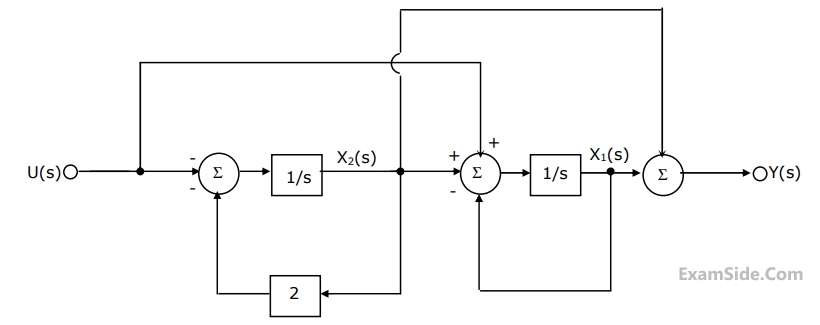
(a) Write down the state variable equations for the system in matrix form
assuming the state vector to be $${\left[ {{x_1}\left( t \right)\,\,{x_2}\left( t \right)} \right]^T}$$
(b) Find out the state transition matrix.
(c) Determine y(t), t ≥ 0, when the initial values of the state at time t = 0 are $${x_1}$$(0) = 1, and $${x_2}$$(0) = 1.
19
The number of comparators required in a 3-bit comparator type ADC is
20
It is required to design a binary mod-5 synchronus counter using AB flip-flops such that the output Q
2Q
1Q
0 changes as $$000 \to 001 \to 010$$ ........and so on. The excitation table for the AB flip-flops is given in the table


(a) Write down the state table for the mod-5 counter.
(b)Obtain simplified SOP expressions for the inputs A2, B2, A1, B1, A0 and B0 in terms of Q2, Q1, Q and their complements.
(c) Hence, complete the circuit diagram for the mod-5 counter given in the figure using minimum number of 2-input NAND-gate only.
21
If the input X$$_3$$, X$$_2$$, X$$_1$$, X$$_0$$ to the ROM in figure 2.12 are 8-4-2-1 BCD numbers, then the outpus are Y$$_3$$,Y$$_2$$, Y$$_1$$, Y$$_0$$ are
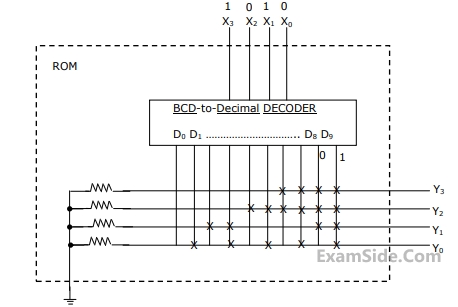
22
4-bit 2’s complement representation of a decimal number is 1000. The number is
23
If the input to the digital circuit (in the figure) consisting of a cascade of 20 XOR-gates is X then the output Y is equal to

24
The gates G
1 and G
2 in figure have propagation delays of 10nsec and 20nsec respectively. If the input V
i makes an abrupt change from logic 0 to 1 at
time t = t
0, then the output waveform V
0 is
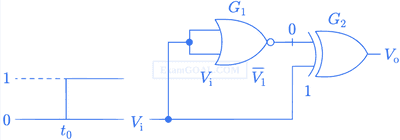
25
The inputs to a digital circuit shown in Figure 9(a) are the external signals A, B and C.
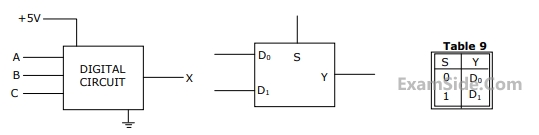
( $$\overline A \,\overline B \,and\,\overline {C\,} $$ and are not available). The +5V power supply (logic 1) and the ground
(logic 0) are also available. The output of the circuit is X = $$\overline A \,B + \,\overline A \,\overline B \,\,\overline {C\,} $$
(a) Write down the output function in its canonical SOP and POS forms.
(b) Implement the circuit using only two 2:1 multiplexers shown in the Figure
where S is the data-select line, $${D_0}\,$$ and $${D_1}\,$$ are the input data lines and Y is the output lines. The function table for the multiplexer is given in table
26
The VSWR can have any value between
27
In an impedance Smith chart, a clockwise movement along a constant resistance circle gives rise to
28
A plane wave is characterized by
$$$\overrightarrow E = \left( {0.5\mathop x\limits^ \cap + \mathop y\limits^ \cap \,{e^{j\pi /2}}} \right){e^{j\omega t - jkz}}.$$$
This wave is
29
Distilled water at $${25^ \circ }C$$ is characterized by $$\sigma = 1.7 \times {10^{ - 4}}$$ mho/m and $$ \in = 78{ \in _0}$$ at a frequency of $$3 GHz$$. Its loss tangent $$\tan \delta $$ is
30
The phase velocity for the $$T{E_{10}}$$ mode in an air-filled rectangular waveguide is
31
A person with a receiver is 5 Km away from the transmitter. What is the distance that this person must move further to detect a 3-dB decrease in signal strength?
32
Consider a linear array of two half - wave dipoles A and B as shown in Fig. The dipoles are $${\lambda \over 4}$$ apart and are excited in such a way that the current on element B lags that on element A by $${90^0}$$ in phase
(a) Obtain the expression for the radiation pattern for E in the XY plane, i.e.,$$\left( {\theta = {{90}^0}} \right)$$.
(b) Sketch the radiation pattern obtained in (a).
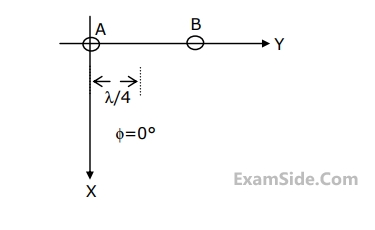
33
The line-of-sight communication requires the transmit and receive antennas to face each other. If the transmit antenna is vertically polarized for best reception the receiver antenna should be
34
Consider a parallel plate waveguide with plate separation d as shown in Fig. The electric and magnetic fields for the TEM mode are given by
$${E_x} = \,{E_0}\,\,{e^{ - j\,k\,z + j\,\omega \,t}},\,{H_y} = {{{E_0}} \over \eta }\,{e^{ - j\,k\,z + j\,\omega \,t}}$$
Where $$k = \,\,\eta \,\omega \,\, \in $$
(a) Determine the surface charge densities $${\rho _s}$$ on the plates at x = 0 and x = d
(b) Determine the surface current densities $$\mathop {{J_s}}\limits^ \to $$ on the same plates.
(c) Prove that $${\rho _s}$$ and $$\mathop {{J_s}}\limits^ \to $$ satisfy the current continuity condition.

35
Consider a parallel plate waveguide with plate separation d as shown in Fig. The electric and magnetic fields for the TEM mode are given by
$${E_x} = \,{E_0}\,\,{e^{ - j\,k\,z + j\,\omega \,t}},\,{H_y} = {{{E_0}} \over \eta }\,{e^{ - j\,k\,z + j\,\omega \,t}}$$
Where $$k = \,\,\eta \,\omega \,\, \in $$
(a) Determine the surface charge densities $${\rho _s}$$ on the plates at x = 0 and x = d
(b) Determine the surface current densities $$\mathop {{J_s}}\limits^ \to $$ on the same plates.
(c) Prove that $${\rho _s}$$ and $$\mathop {{J_s}}\limits^ \to $$ satisfy the current continuity condition.

36
Consider a parallel plate waveguide with plate separation d as shown in Fig. The electric and magnetic fields for the TEM mode are given by
$${E_x} = \,{E_0}\,\,{e^{ - j\,k\,z + j\,\omega \,t}},\,{H_y} = {{{E_0}} \over \eta }\,{e^{ - j\,k\,z + j\,\omega \,t}}$$
Where $$k = \,\,\eta \,\omega \,\, \in $$
(a) Determine the surface charge densities $${\rho _s}$$ on the plates at x = 0 and x = d
(b) Determine the surface current densities $$\mathop {{J_s}}\limits^ \to $$ on the same plates.
(c) Prove that $${\rho _s}$$ and $$\mathop {{J_s}}\limits^ \to $$ satisfy the current continuity condition.

37
The intrinsic carrier concentration of silicon sample at 300oK is $$1.5\times10^{16}/m^3$$. If after doping, the number of majority carriers is $$5\times10^{20}/m^3$$ , minority carrier density is
38
The band gap of silicon at 300 K is
39
In the figure, a silicon diode is carrying a constant current of 1 mA. When the
temperature of the diode is 20°C, V
D is found to be 700 mV. If the temperature
rises to 40°C, V
D becomes approximately equal to
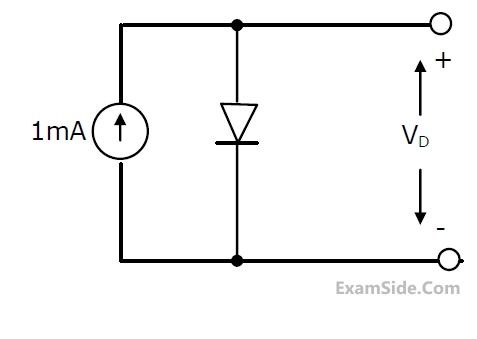
40
If the transistor in Figure is in saturation, then

41
The contents of Register (B) and Accumulator (A) of 8085 microprocessor are 49H and 3AH respectively. The contents of A and the status of carry flag (CY) and sign flag (S) after executing SUB B instructions are
42
Consider the following assembly language program.

The execution of the above program in an 8085 microprocessor will result in
43
The switch in Fig. has been in position $$1$$ for a long time and is then moved to position $$2$$ at $$t\, = \,0$$.
(a) Determine $${V_C}\left( {{0^ + }} \right)$$ and $${I_{_L}}\left( {{0^ + }} \right)$$
(b) Determine $${{d{V_C}\left( t \right)} \over {dt}}\,\,$$ at $$t\, = \,{0^ + }$$
(c) Determine $${{V_C}\left( t \right)}$$ for $$t > 0$$
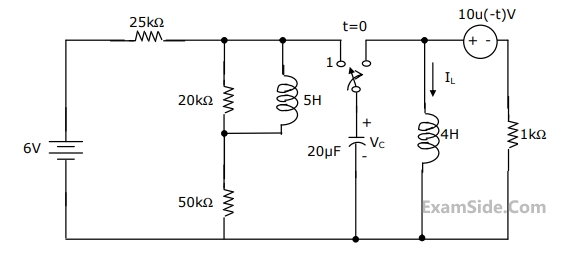
44
For network shown in Fig. $$R\, = \,1\,k\Omega $$
$${L_1} = 2\,H,\,{L_2} = 5\,H,\,{L_3}\, = \,1H,{L_4} = 4H\,\,\,$$ and $$C - 0.2\,\,\mu F.$$. The mutual inductances are $${M_{12}} = 3\,H$$ and $${M_{34}} = 2\,H$$.
Determine
(a) the equivalent inductance for the combination of $${L_3}$$ and $${L_4}$$,
(b) the equivalent inductance across the points A and B in the network,
(c) the resonant frequency of the network.
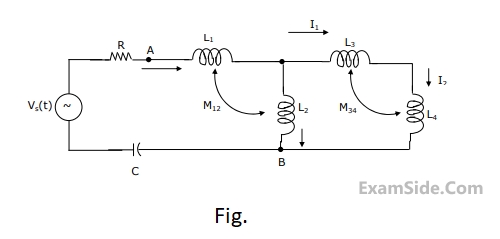
45
Consider the network in Fig.
(a) Find its short-circuit admittance parameters.
(b) Find the open-ciruit impedance $${Z_{22}}$$.
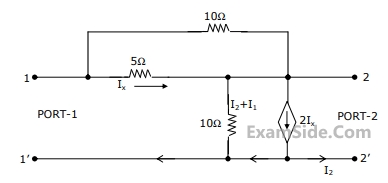
46
The dependent current source shown in Figure
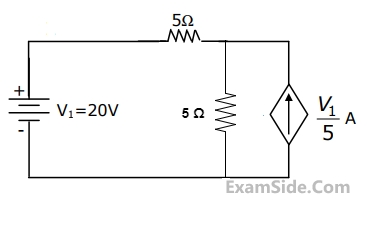
47
In the network of Figure, the maximum power is delivered to RL if its value is
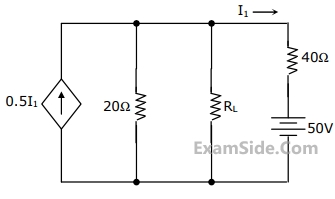
48
In figure, the switch was closed for a long time before opening at t = 0. the
voltage V
x at t = 0
+ is
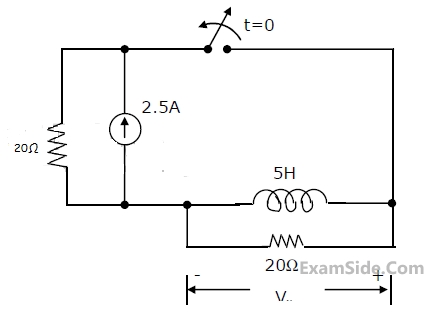
49
If the 3-phase balanced source in Fig. delivers 1500 W at a leading power
factor of 0.844, then the value of Z
L (in ohm) is approximately
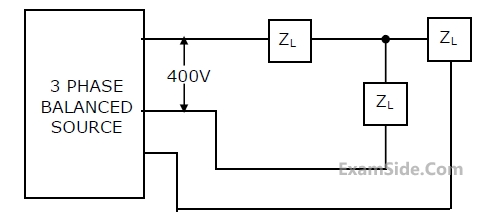
50
The differential equation for the current i(t) in the circuit of Fig. is

51
The Fourier transform F $$\left\{ {{e^{ - t}}u(t)} \right\}$$ is equal to $${1 \over {1 + j2\pi f}}$$. Therefore, $$F\left\{ {{1 \over {1 + j2\pi t}}} \right\}$$ is
52
The Laplace transform of a continuous - time signal x(t) is $$X\left( s \right) = {{5 - s} \over {{s^2} - s - 2}}$$. If the Fourier transform of tyhis signal exists, then x(t) is
53
Convolution of x(t + 5) with impulse function $$\delta \left( {t\, - \,7} \right)$$ is equal to
54
A deterministic signal x(t) = $$\cos (2\pi t)$$ is passed through a differentiator as shown in
Figure.

(a) Determine the autocorrelation R
xx ($$\tau $$) and the power spectral density S
xx(f).
(b) Find the output power spectral density S
yy( f ).
(c) Evaluate R
xy(0) and R
xy(1/4).
55
If the impulse response of a discrete-time system is $$h\left[ n \right]\, = \, - {5^n}\,\,u\left[ { - n\, - 1} \right],$$ then the system function $$H\left( z \right)\,\,\,$$ is equal to
56
Consider a sampled signal $$y\left( t \right) = 5 \times {10^{ - 6}}\,x\left( t \right)\,\,\sum\limits_{n = - \infty }^{ + \infty } {\delta \left( {t - n{T_s}} \right)} $$
where $$x\left( t \right) = 10\,\,\cos \,\left( {8\pi \times {{10}^3}} \right)\,\,t$$ and
$${T_s} = 100\,\,\mu \sec .$$ When $$y\left( t \right)$$ is passed through an ideal low-pass filter with a cutoff frequency of 5 KHz, the output of the filter is
57
A linear phase channel with phase delay $${\tau _p}$$ and group delay $${\tau _g}$$ must have
58
In Fig. m(t) = $$ = {{2\sin 2\pi t} \over t}$$, $$s(t) = \cos \,200\pi t\,\,andn(t) = {{\sin 199\pi t} \over t}$$.
The output y(t) will be
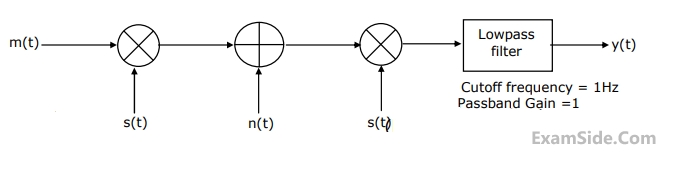
59
A signal x(t) = 100 cos $$(24\pi \times {10^3})$$ t is ideally sampled with a sampling period of 50 $$\mu \sec $$ and then passed through an ideal low pass filter with cutoff frequency of 15 KHz. Which of the following frequencies is/ are present at the filter output?
60
Which of the following cannot be the Fourier series expansion of a periodic
signal?




 (a) Write down the state variable equations for the system in matrix form
assuming the state vector to be $${\left[ {{x_1}\left( t \right)\,\,{x_2}\left( t \right)} \right]^T}$$
(a) Write down the state variable equations for the system in matrix form
assuming the state vector to be $${\left[ {{x_1}\left( t \right)\,\,{x_2}\left( t \right)} \right]^T}$$





 ( $$\overline A \,\overline B \,and\,\overline {C\,} $$ and are not available). The +5V power supply (logic 1) and the ground
(logic 0) are also available. The output of the circuit is X = $$\overline A \,B + \,\overline A \,\overline B \,\,\overline {C\,} $$
( $$\overline A \,\overline B \,and\,\overline {C\,} $$ and are not available). The +5V power supply (logic 1) and the ground
(logic 0) are also available. The output of the circuit is X = $$\overline A \,B + \,\overline A \,\overline B \,\,\overline {C\,} $$






 The execution of the above program in an 8085 microprocessor will result in
The execution of the above program in an 8085 microprocessor will result in











 The execution of the above program in an 8085 microprocessor will result in
The execution of the above program in an 8085 microprocessor will result in
