1
A common-emitter amplifier with an external capacitor C
C connected across the base and the collector of the transistor is shown in Fig.

Transistor data gm = 5mA/V, $${r_\pi }\, = \,200K\Omega, $$ $${C_\pi }\, = \,1.5$$ pF and $$C\mu \, = \,0.5$$ pF determine the upper cutoff frequency fH of the amplifier
2
A Darlington stage is shown in the figure, if the transconductance of q
1 is g
m1 and q
2 is g
m2, then the overall transconductance
$$g\matrix{
c \cr
m \cr
} \left[ { \buildrel \Delta \over = {{{i_c}^c} \over {{v_{be}}^c}}} \right]$$ is given by

3
Match the following.
Group - I
(a)Cascode amplifier
(b)Differential Amplifier
(c)Darlington pair common-collector Amplifier
Group - II
(1)does not provide current gain
(2)is a wide band Amplifier
(3)has very low input impedance Emitter Amplifier and very high current gain
(4)has very high input impedance and very high current gain
(5)Provides high common mode voltage Rejection
4
An npn transistor has a beta cut-off frequency $${f_\beta }$$ of 1MHz and Common Emitter short circuit low frequency current gain $${\beta _o}$$ of 200. The unity gain frequency $${f_T}$$ and the alpha cut-off frequency $${f_\alpha }$$ respectively are
5
In the circuit shown in Fig. is a finite gain amplifier with a gain of K, a very large input impedance, and a very low output impedance. The input impedance of the feedback amplifier with the feedback impedance Z conducted as shown will be

6
A JEFT with V
P = -4V and I
Dss = 12mA is used in the circuit shown in Fig. Assuming the device to be operating in saturation, determine I
D, V
DS and V
GS

7
Value of R in the oscillator shown in the given figure. So chosen that it just oscillates at an angular frequencies of' "$$\omega $$". The value of "$$\omega $$" and the required value of R will respectively be

8
The circuit shown in the figure is that of

9
The number of bits in a binary PCM system is increased from n to n+1. As a result, the signal to quantization noise ratio will improve by a factor
10
A system having an open loop transfer function
$$G\left(s\right)=\frac{K\left(s+3\right)}{s\left(s^2+2s+2\right)}$$
is used in a
control system with unity negative feedback. Using the Routh-Hurwitz criterion,
find the range of values of 'K' for which the feedback system is stable.
11
Obtain a state space representation in diagonal form for the following system
$$${{{d^3}y} \over {d{t^3}}} + 6{{{d^2}y} \over {d{t^2}}} + 11{{dy} \over {dt}} + 6y = 6u\left( t \right)$$$
12
Given the Boolean function F in three variables R, S and T as
F=$$\,\overline R \,S\overline T + R\overline {S\,} T + RST$$
(a) Express F in the minimum sum-of-products from.
(b) Express F in the minimum product-of-sums from.
(c) Assuming that both true and complement froms of the input variables are avialable, draw a cicruit to implement F using the minimum number of 2input NAND gates only.
13
Its is desired to generate the following three Boolean functions.
$$\eqalign{
& {F_1} = a\,\overline b \,c + \overline a \,b\overline c + bc \cr
& {F_2} = \,a\,\overline b \,c + ab + \overline a \,b\overline c \cr
& {F_3} = \,\overline a \,\overline b \,\overline c + abc + \overline a c \cr} $$
By using an OR gate array as shown in figure where $${P_{1\,}}\,to\,{P_5}$$ are the product terms in one or more of the variables a, $$\overline a $$, b, $$\,\overline b $$, c and $$\overline c $$.

14
Each cell of a static Random Access Memory Contains
15
A 12-bit ADC is operating with a 1$$\mu $$ sec clock period and the total conversion time is seen to be 14 $$\mu $$ sec. The ADC must br of the
16
A 4-bit shift register, which shifts 1 bit to the right at every clock pulse, is intialized to values (1000) for (Q
0Q
1Q
2Q
3). The D input is derived from Q
0, Q
2 and Q
3 through two XOR gates as shown in figure.

(a) Write the 4-bit values (Q0Q1Q2Q3) after each clock pulse till the pattern (1000) reappears on (Q0Q1Q2Q3).
(b) To what values should the shift register be intialized so that the pattern (1001) occurs after the first clock pulse?
17
A state machine is required to cycle through the following sequence of states:

One possible implementation of the state machine is shown figure. Specify what signals should be applied to each of the multiplexer inputs

18
Some unknown material has a conductivity of $${10^{ 6}}$$ $$mho/m$$ and a permeability of $$4\pi \times {10^{ - 7}}\,\,\,\,\,H/m.$$ The skin depth for the material at $$1GHz$$ is
19
A lossless transmission line having 50 $$\Omega $$ characteristic impedance and lenght $$\lambda /4$$ is short ciruited at one end and connected to an ideal voltage sourec of 1 V at the other end. The current drawn from the voltage source is
20
The capacitance per unit length and the characteristic impedance of a lossless transmission line are C and $$Z_0$$ respectively. The velocity of a traveling wave on the transmission line is
21
A uniform plane wave in air is normally incident on an infinitely thick slab. If the reflective index of the glass slab is 1.5, then the percentage of the incident power that is reflected from the air-glass interface is
22
A metal sphere with 1 m radius and a surface charge density of 10 Coulombs/m2 is enclosed in
a cube of 10 m side. The total outward electric displacement normal
to the surface of the cube is
23
A uniform plane wave having parallel polarization is obliquely incident on an air - dielectric interface as shown in Fig. If the wave has an electric field $$E = 10\,\,V/m$$, find
(i) The angle of incidence $${\theta _i}$$ for which there is no reflection of the wave.
(ii) The surface charge density at the interface.
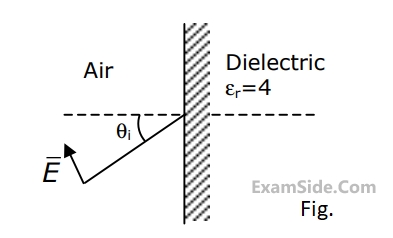
24
A transverse electromagnetic wave with circular polarization is received by a dipole antenna. Due to polarization mismatch, the power transfer efficiency from the wave to the antenna is reduced to about
25
A 1 km long microwave link uses two antennas each having 30dB gain. If the power transmitted by one antenna is 1 W at 3 GHz, the power received by the other antenna is approximately
26
In an air-filled rectangular waveguide, the vector electric field is given by
$$\mathop E\limits^ \to = \cos \,(20\,\pi \,y)\,\exp \,\,\left[ { - j\left( {{{40\,\,\pi } \over 3}} \right)\,z\, + j\,\omega \,t} \right]\,\hat i\,\,\,V/m$$
Find the vector magnetic field and the phase velocity of the wave inside the waveguide.
27
Two isotropic antennas A and B from an array as shown in Fig. The currents fed to the two antennas are $${{\rm I}_0}\,\angle 0$$ and $${{\rm I}_0}\,\angle \alpha $$ respectively. What should be the value of $$\alpha $$ so that the radiation pattern has a null at $$\theta = {30^ \circ }$$. Find the direction of the maximum radiation for that value of $$\alpha $$ and draw the radiation pattern. ($$\lambda \,\,$$ is the wavelength of operation)

28
The inverse laplace transform of the function $${{s + 5} \over {\left( {s + 1} \right)\left( {s + 3} \right)}}$$ is _______________.
29
The following sequence of instructions are executed by an 8085 microprocessor:
1000: LXI SP< 27FF
1003: CALL 1006
1006: POP H
The contents of the stack pointer (SP) and the HL register pair on completion or execution of these instructions are.
30
The total number of memory accesses involved (inclusive of the op-code fetch) when an 8085 processor executes, the instruction LDA 2003 is
31
In Fig., A
1, A
2 and A
3 are ideal ammeters. If A
2 and A
3 read 3 A and 4 A respectively, then A
1 should read
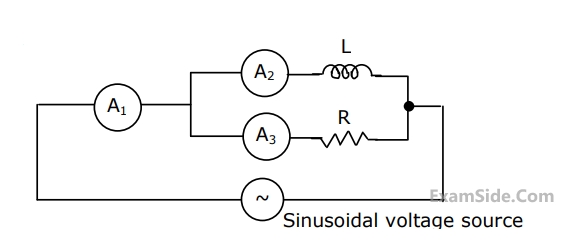
32
In the circuit of Fig., assume that the diodes are ideal and the meter is an average indicating ammeter. The ammeter will read
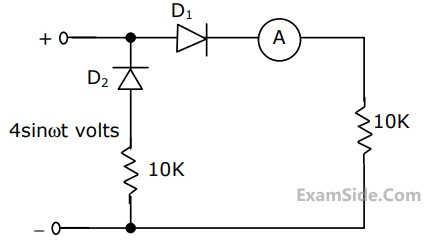
33
Find the input resistance $${R_{in}}$$ of the infinite section resistive network shown in Fig.

34
The open circuit impedance matrix $${Z_{OC}}$$ of a three-terminal two-port network with A as the input terminal, B as the output terminal, and C as the common terminal, is given as
$$$\left[ {{Z_{OC}}} \right] = \left[ {\matrix{
2 & 5 \cr
3 & 7 \cr
} } \right]$$$
Write down the short circuit admittance matrix $${{Y_{SC}}}$$ of the network viewed as a two-port network, but now taking B as the input terminal, C as the output terminal and A as the common terminal.
35
The voltage VC1, VC2 and VC3 across the capacitors in the circuit in Fig., under steady state, are respectively
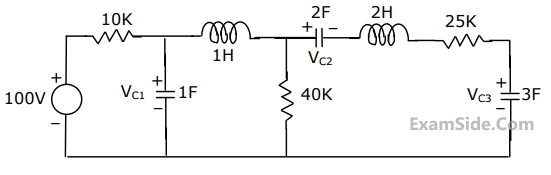
36
The number of independent loops for a network with n nodes and b branches is
37
Refer to the circuit shown in Fig.
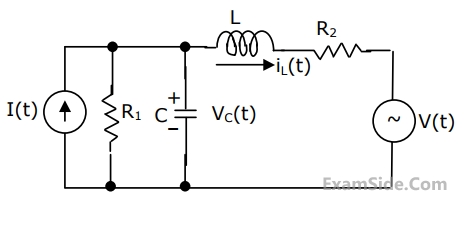
Choosing the voltage v
C(t) across capacitor, and the current i
L(t) through the inductor as state variable,i.e.,
$$$\left[\mathrm x\left(\mathrm t\right)\right]\;=\;\begin{bmatrix}{\mathrm v}_\mathrm C\left(\mathrm t\right)\\{\mathrm i}_\mathrm L\left(\mathrm t\right)\end{bmatrix}$$$
Write the state equation in the form $$\frac{\operatorname d\left[x\left(t\right)\right]}{\operatorname dt}\;=\;\left[A\right]\left[x\left(t\right)\right]\;+\;\left[B\right]\left[u\left(t\right)\right]$$ and find [A], [B] and [u(t)].
38
In the circuit shown in Fig (a) - (c), assuming initial voltages across capacitors and current through the inductors to be zero at the time of switching (t=0), then at any time t>0.
Match each of the items of Set 1, with the appropriate item of the Set 2.

Set 2
(1) current increases monotonically with time
(2) current decreases monotonically with time
(3) current remains constant at V/R
(4) current first increases, then decreases
(5) no current can ever flow
39
In the circuit shown in Fig., it is known that the variable current source I absorbs power.Find I (in magnitude and direction) so that it receives maximum power and also find the amount of power absorbed by it.
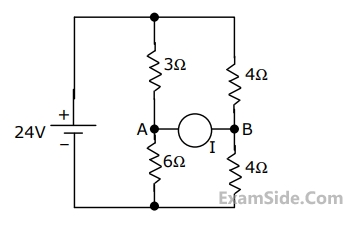
40
The inverse Laplace transform of the function $${{s + 5} \over {\left( {s + 1} \right)\left( {s + 3} \right)}}$$ is
41
The autocorrelation function of an energy signal has
42
A system having a unit impulse response $$h\left( n \right)$$ = $$u\left( n \right)$$ is excited by a signal $$x\left( n \right)$$ $$ = \,{\alpha ^n}\,\,u\left( n \right).\,$$ Determine the output $$y\left( n \right)$$
43
In the linear time-invariant system shown in Fig. 1, blocks labeled D represent unit delay elements. Find the expression for $$y\left( n \right),$$ and also the transfer function $${{Y\left( z \right)} \over {X\left( z \right)}}$$ in the $$z$$-domain.

44
A rectangular pulse of duration T is applied to a filter matched to this input. The output of the filter is a
45
A signal 3 sin $$\left( {\pi \,\,{f_0}t} \right) + \,5\,\,\cos \,\,\,(3\pi \,\,{f_0}t)$$ is applied to an RC low pass filter of 3 dB cutoff frequency $${f_0}$$. Determine and plot the output power spectrum and aslo calculate the total input and output normalized power.
46
An input signal A exp $$\left( { - \alpha \,t} \right)$$ u(t) with $$\alpha > 0$$ is applied to a causal filter, the impulse response of which is A exp $$\,( - \alpha \,\,t)$$. Determine the filter output, sketch it as a function of time and lable the important points.
47
The Fourier transform of a real valued time signal has
48
The trigonometric Fourier series of an even function of time does not have the
















 Choosing the voltage vC(t) across capacitor, and the current iL(t) through the inductor as state variable,i.e.,
$$$\left[\mathrm x\left(\mathrm t\right)\right]\;=\;\begin{bmatrix}{\mathrm v}_\mathrm C\left(\mathrm t\right)\\{\mathrm i}_\mathrm L\left(\mathrm t\right)\end{bmatrix}$$$
Write the state equation in the form $$\frac{\operatorname d\left[x\left(t\right)\right]}{\operatorname dt}\;=\;\left[A\right]\left[x\left(t\right)\right]\;+\;\left[B\right]\left[u\left(t\right)\right]$$ and find [A], [B] and [u(t)].
Choosing the voltage vC(t) across capacitor, and the current iL(t) through the inductor as state variable,i.e.,
$$$\left[\mathrm x\left(\mathrm t\right)\right]\;=\;\begin{bmatrix}{\mathrm v}_\mathrm C\left(\mathrm t\right)\\{\mathrm i}_\mathrm L\left(\mathrm t\right)\end{bmatrix}$$$
Write the state equation in the form $$\frac{\operatorname d\left[x\left(t\right)\right]}{\operatorname dt}\;=\;\left[A\right]\left[x\left(t\right)\right]\;+\;\left[B\right]\left[u\left(t\right)\right]$$ and find [A], [B] and [u(t)].


