The following two signed 2's complement numbers (multiplicand M and multiplier Q ) are being multiplied using Booth's algorithm :
M : 1100110111101101 and Q : 1010010010101010
The total number of addition and subtraction operations to be performed is ________ (Answer in integer)
Let $X$ be a 3-variable Boolean function that produces output as ' 1 ' when at least two of the input variables are ' 1 '. Which of the following statement(s) is/are CORRECT, where $a, b, c, d, e$ are Boolean variables?
For a Boolean variable x, which of the following statements is/are FALSE?
Which one of the following must always be TRUE?
$$x \ne 0 = x,\,\,x \ne 1 = \overline x ,\,\,x \ne x = 0$$ and $$x \ne \overline x = 1.$$ Then $$x \ne y$$ is equivalent to
Which of the following is/are true for the Boolean variables $$𝑃, 𝑄$$ and $$𝑅$$?
$$b$$ where $$x, a, b$$ are inputs and $$y$$ is the output.
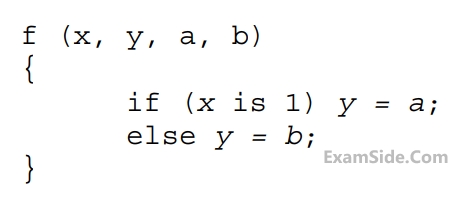
Which one of the following digital logic blocks is the most suitable for implementing this function?
$$F\left( {P,\,Q,\,R,\,S} \right) = PQ + \overline P QR + \overline P Q\overline R S.$$
The minimal sum-of-products form of $$F$$ is
$$\left( {P + \overline Q + \overline R } \right).\left( {P + \overline Q + R} \right).\left( {P + Q + \overline R } \right)$$ is
Then $${f_2}$$ is

$$F\left( {w,\,x,\,y,\,z} \right) = \sum {\left( {1,\,3,\,4,\,6,\,9,\,11,\,12,\,14} \right)} $$ the function is
Which of the following Boolean algebraic equation(s) is/are CORRECT?
Consider 4-variable functions $f1, f2, f3, f4$ expressed in sum-of-minterms form as given below.
$f1 = \sum(0,2,3,5,7,8,11,13)$
$f2 = \sum(1,3,5,7,11,13,15)$
$f3 = \sum(0,1,4,11)$
$f4 = \sum(0,2,6,13)$

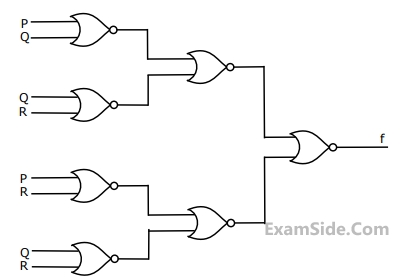
With respect to the circuit given above, which of the following options is/are CORRECT?
Consider a Boolean expression given by $F(X, Y, Z) = \Sigma(3,5,6,7)$.
Which of the following statements is/are CORRECT?
Consider a Boolean function f(w, x, y, z) such that
f(w, 0, 0, z) = 1
f(1, x, 1, z) = x + z
f(w, 1, y, z) = wz + y
The number of literals in the minimal sum-of-products expression of f is ______
Consider the following Boolean expression.
$$F = (X + Y + Z)(\overline X + Y)(\overline Y + Z)$$
Which of the following Boolean expressions is/are equivalent to $$\overline F$$ (complement of F)?

Which one of the following minterm lists represents the circuit given above?
f1 = Σ(0, 2, 5, 8, 14),
f2 = Σ(2, 3, 6, 8, 14, 15),
f3 = Σ(2, 7, 11, 14)
For the following circuit with one AND gate and one XOR gate, the output function f can be expressed as :
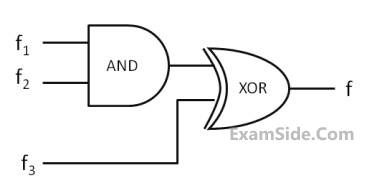
Which one of the following is NOT CORRECT?
$$f\left( {w,x,y,z} \right) = \sum {\left( {0,2,4,5,6,10} \right)} $$ _________________.
$$\eqalign{ & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( {S1} \right)\,\,\,\,F = \sum {\left( {4,5,6} \right)} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( {S2} \right)\,\,\,\,F = \sum {\left( {0,1,2,3,7} \right)} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( {S3} \right)\,\,\,\,F = \sum {\Pi \left( {4,5,6} \right)} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( {S4} \right)\,\,\,\,F = \sum {\Pi \left( {0,1,2,3,7} \right)} \cr} $$
Which of the following is true?
Consider the operations
$$f\left( {x,y,z} \right) = X'YZ + XY' + Y'Z'$$ and$$g\left( {x,y,z} \right) = X'YZ + X'YZ' + XY$$.
Which one of the following is correct?
The binary operator $$ \ne $$ is defined by the following truth table.
| p | q | p$$ \ne $$q |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Which one of the following is true about the binary operator $$ \ne $$?
$$F\left( {P,Q} \right) = \left( {1 \oplus P} \right) \oplus \left( {P \oplus Q} \right) \oplus \left( {P \oplus Q} \right) \oplus \left( {Q \oplus 0} \right)$$
The equivalent expression for $$F$$ is
$$(P)\,\,\,$$ $$x'y'z' + w'xy' + wy'z + xz$$
$$(Q)\,\,\,$$ $$w'y'z' + wx'y' + xz$$
$$(R)\,\,\,$$ $$w'y'z' + wx'y' + xyz + xy'z$$
$$(S)\,\,\,$$ $$x'y'z' + wx'y' + w'y$$


have the following for $$x, y, z$$ and $$w,$$ respectively.

$${f_1}\left( {w,\,x,\,y,\,z} \right) = \sum {8,9,10} $$
$${f_2}\left( {w,\,x,\,y,\,z} \right) = \sum {7,8,12,13,18,15} $$
$$f\left( {w,\,x,\,y,\,z} \right) = \sum {\left( {8,9} \right)} $$
The function $${f_3}$$ is

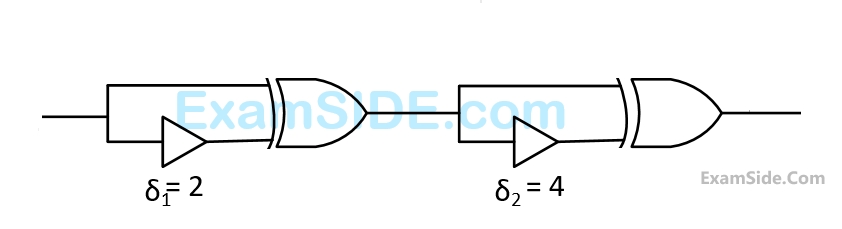
The non-inverting buffers have delays $${\delta _1} = 2$$ $$ns$$ and $${\delta _2} = 4$$ $$ns$$ as shown in the figure. Both $$XOR$$ gates and all wires have zero delay. Assume that all gate inputs, outputs and wires are stable at logic level $$0$$ at time$$0.$$ If the following waveform is applied at input $$A$$, how many transition(s) (change of logic levels) occurs(s) at $$B$$ during the interval from $$0$$ to $$10$$ $$ns?$$


Implement the circuit using one $$4$$ to $$1$$ Multiplexor, one $$2$$-input Exclusive $$OR$$ gate, one $$2$$-input $$AND$$ gate, one $$2$$-input $$OR$$ gate and one Inverter.
$$f\left( {A,B,C,D} \right) = \sum d \left( {3,11,12,14} \right)$$
Where $$m$$ and $$d$$ denote the minterms and don't cares respectively.
$$f = ABC + \overline A \,\overline B \,\overline C .$$
$$f=AB+BC+CA$$ can be realized using only $$4:1$$ multiplexer.