GATE ME 2014 Set 3 | Simple Stress and Strain Question 21 | Strength of Materials

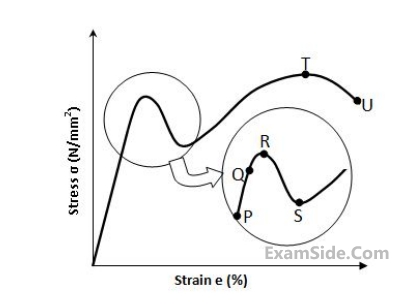
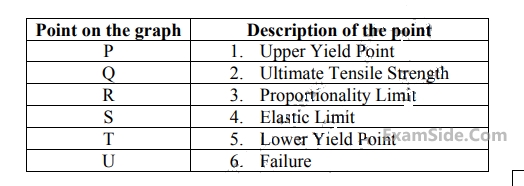
The stress-strain curve for mild steel is shown in the figure given below. Choose the correct option referring to both figure and table GATE ME 2014 Set 3 Strength of Materials - Simple Stress and Strain Question 25 English 1

GATE ME 2014 Set 3 Strength of Materials - Simple Stress and Strain Question 25 English 1

GATE ME 2014 Set 3 Strength of Materials - Simple Stress and Strain Question 25 English 2

$$P - 1,\,Q - 2,\,R - 3,\,S - 4,\,T - 5,\,U - 6$$

$$P - 3,\,Q - 1,\,R - 4,\,S - 2,\,T - 6,\,U - 5$$

$$P - 3,\,Q - 4,\,R - 1,\,S - 5,\,T - 2,\,U - 6$$

$$P - 4,\,Q - 1,\,R - 5,\,S - 2,\,T - 3,\,U - 6$$

GATE ME 2013

MCQ (Single Correct Answer)

-0.3

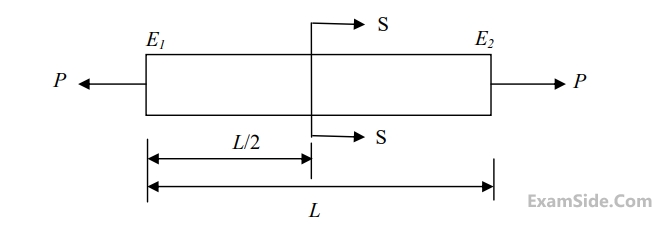
A rod of length $$L$$ having uniform cross-sectional area $$A$$ is subjected to a tensile force $$P$$ as shown in the figure below. If the Young’s modulus of the material varies linearly from $${E_1}$$ to $${E_2}$$ along the length of the rod, the normal stress developed at the section $$-$$ $$SS$$ is GATE ME 2013 Strength of Materials - Simple Stress and Strain Question 30 English

GATE ME 2013 Strength of Materials - Simple Stress and Strain Question 30 English

$${P \over A}$$

$${{P\left( {{E_1} - {E_2}} \right)} \over {A\left( {{E_1} + {E_2}} \right)}}$$

$${{P{E_2}} \over {A{E_1}}}$$

$${{P{E_1}} \over {A{E_2}}}$$

GATE ME 2007

MCQ (Single Correct Answer)

-0.3

A steel rod of length $$L$$ and diameter $$D$$, fixed at both ends, is uniformly heated to a temperature rise of $$\Delta T.$$ The Young's modulus is $$E$$ and the coefficient of linear expansion is $$'\alpha '\,.$$ The thermal stress in the rod is

$$0$$

$$\alpha \Delta \,T$$

$$E\alpha \Delta \,T$$

$$E\alpha \Delta \,TL$$

GATE ME 2004

MCQ (Single Correct Answer)

-0.3

In terms of Poisson's ratio $$\left( \mu \right)$$ the ratio of Young's Modulus $$(E)$$ to Shear Modulus $$(G)$$ of elastic materials is

$$2\left( {1 + \mu } \right)$$

$$2\left( {1 - \mu } \right)$$

$${1 \over 2}\left( {1 + \mu } \right)$$

$${1 \over 2}\left( {1 - \mu } \right)$$

Previous Next

Questions Asked from Marks 1

GATE ME 2022 Set 2 (1) GATE ME 2017 Set 2 (1) GATE ME 2017 Set 1 (2) GATE ME 2015 Set 2 (1) GATE ME 2014 Set 1 (3) GATE ME 2014 Set 4 (2) GATE ME 2014 Set 2 (1) GATE ME 2014 Set 3 (1) GATE ME 2013 (1) GATE ME 2007 (1) GATE ME 2004 (2) GATE ME 2003 (1) GATE ME 1995 (1) GATE ME 1992 (1)

GATE ME Subjects

Engineering Mechanics

Machine Design

Strength of Materials

Heat Transfer

Production Engineering

Industrial Engineering

Turbo Machinery

Theory of Machines

Engineering Mathematics

Fluid Mechanics

Thermodynamics

General Aptitude