Strength of Materials
1
GATE ME 2013
MCQ (Single Correct Answer)
+1
-0.3
A rod of length $$L$$ having uniform cross-sectional area $$A$$ is subjected to a tensile force $$P$$ as shown in the figure below. If the Young’s modulus of the material varies linearly from $${E_1}$$ to $${E_2}$$ along the length of the rod, the normal stress developed at the section $$-$$ $$SS$$ is
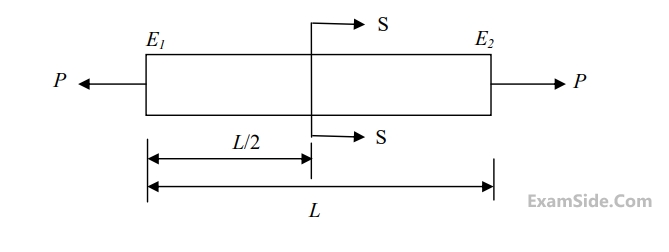

2
GATE ME 2007
MCQ (Single Correct Answer)
+1
-0.3
A steel rod of length $$L$$ and diameter $$D$$, fixed at both ends, is uniformly heated to a temperature rise of $$\Delta T.$$ The Young's modulus is $$E$$ and the coefficient of linear expansion is $$'\alpha '\,.$$ The thermal stress in the rod is
3
GATE ME 2004
MCQ (Single Correct Answer)
+1
-0.3
In terms of Poisson's ratio $$\left( \mu \right)$$ the ratio of Young's Modulus $$(E)$$ to Shear Modulus $$(G)$$ of elastic materials is
4
GATE ME 2004
MCQ (Single Correct Answer)
+1
-0.3
A uniform, slender cylindrical rod is made of a homogeneous and isotropic material. The rod rests on a frictionless surface. The rod is heated uniformly. If the radial and longitudinal thermal stresses are represented by $${\sigma _r}$$ and $${\sigma _z}$$ respectively, then
Questions Asked from Marks 1
GATE ME Subjects
Engineering Mechanics
Machine Design
Strength of Materials
Heat Transfer
Production Engineering
Industrial Engineering
Turbo Machinery
Theory of Machines
Engineering Mathematics
Fluid Mechanics
Thermodynamics
General Aptitude