ExamSIDE
Questions (Powered by ExamGOAL)
Theory of Computation
Finite Automata and Regular Language
Marks 1Marks 2Marks 5
Push Down Automata and Context Free Language
Marks 1Marks 2
Undecidability
Marks 1Marks 2
Recursively Enumerable Language and Turing Machine
Marks 1Marks 2
Previous Next
1
GATE CSE 2007
MCQ (Single Correct Answer)
+2
-0.6
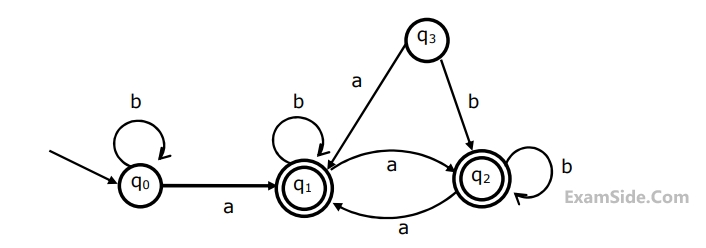
Consider the following finite state automation GATE CSE 2007 Theory of Computation - Finite Automata and Regular Language Question 66 English

The minimum state automation equivalent to the above $$FSA$$ has the following number of states

A
$$1$$
B
$$2$$
C
$$3$$
D
$$4$$
2
GATE CSE 2006
MCQ (Single Correct Answer)
+2
-0.6
If $$s$$ is a string over $${\left( {0 + 1} \right)^ * }$$ then let $${n_0}\left( s \right)$$ denote the number of $$0'$$ s in $$s$$ and $${n_1}\left( s \right)$$ the number of $$1'$$s in $$s.$$ Which one of the following languages is not regular?
A
$$L = \left\{ {s \in {{\left( {0 + 1} \right)}^ * }\left| {{n_0}\left( s \right)\,\,} \right.} \right.$$ is a $$3$$-digit prime$$\left. \, \right\}$$
B
$$L = \left\{ {s \in {{\left( {0 + 1} \right)}^ * }\left| {\,\,} \right.} \right.$$ for every prefix $$s'$$ of $$s.$$ $$\,\left| {{n_0}\left( {{s^,}} \right) - {n_1}\left( {{s^,}} \right)\left| { \le \left. 2 \right\}} \right.} \right.$$
C
$$L = \left\{ {s \in {{\left( {0 + 1} \right)}^*}\left\| {{n_0}\left( s \right) - {n_1}\left( s \right)\left| { \le \left. 4 \right\}} \right.} \right.} \right.$$
D
$$L = \left\{ {s \in {{\left( {0 + 1} \right)}^ * }} \right.\left| {{n_0}\left( s \right)} \right.$$ mod $$7 = {n_1}\left( s \right)$$ mod $$5 = \left. 0 \right\}$$
3
GATE CSE 2006
MCQ (Single Correct Answer)
+2
-0.6
Consider the regular language $$L = {\left( {111 + 11111} \right)^ * }.$$ The minimum number of states in any $$DFA$$ accepting this language is
A
$$3$$
B
$$5$$
C
$$8$$
D
$$9$$
4
GATE CSE 2005
MCQ (Single Correct Answer)
+2
-0.6
Consider the machine $$M:$$ The language recognized by $$M$$ is: GATE CSE 2005 Theory of Computation - Finite Automata and Regular Language Question 48 English
A
$$\left\{ {w\,\, \in \,\left\{ {a,b} \right\}{}^ * \left| \, \right.} \right.$$ every $$a$$ in $$w$$ is followed by exactly two $$\left. {b's} \right\}$$
B
$$\left\{ {w\,\, \in \,\left\{ {a,b} \right\}{}^ * \left| \, \right.} \right.$$ every $$a$$ in $$w$$ is followed by at least two $$\left. {b's} \right\}$$
C
$$\left\{ {w\,\, \in \,\left\{ {a,b} \right\}{}^ * \left| \, \right.} \right.$$ $$w$$ contains the substring $$\,\left. {'abb'\,\,} \right\}\,$$
D
$$\left\{ {w\,\, \in \,\left\{ {a,b} \right\}{}^ * \left| \, \right.} \right.$$ $$w$$ does not contain $$'aa'$$ as a substring$$\left. \, \right\}$$
Previous Next
Questions Asked from Marks 2
GATE CSE 2025 Set 2 (2) GATE CSE 2025 Set 1 (3) GATE CSE 2024 Set 2 (2) GATE CSE 2024 Set 1 (2) GATE CSE 2023 (1) GATE CSE 2021 Set 2 (3) GATE CSE 2021 Set 1 (1) GATE CSE 2020 (1) GATE CSE 2019 (1) GATE CSE 2018 (2) GATE CSE 2016 Set 2 (2) GATE CSE 2016 Set 1 (1) GATE CSE 2015 Set 2 (3) GATE CSE 2015 Set 1 (2) GATE CSE 2014 Set 2 (2) GATE CSE 2014 Set 1 (1) GATE CSE 2013 (1) GATE CSE 2012 (1) GATE CSE 2011 (2) GATE CSE 2010 (2) GATE CSE 2009 (2) GATE CSE 2008 (3) GATE CSE 2007 (4) GATE CSE 2006 (2) GATE CSE 2005 (1) GATE CSE 2004 (1) GATE CSE 2003 (2) GATE CSE 2002 (2) GATE CSE 2001 (2) GATE CSE 2000 (1) GATE CSE 1998 (1) GATE CSE 1997 (1) GATE CSE 1995 (2) GATE CSE 1994 (2) GATE CSE 1992 (2) GATE CSE 1991 (1) GATE CSE 1990 (1) GATE CSE 1989 (1)
GATE CSE Subjects
Theory of Computation
Operating Systems
Algorithms
Digital Logic
Database Management System
Data Structures
Computer Networks
Software Engineering
Compiler Design
Web Technologies
General Aptitude
Discrete Mathematics
Programming Languages
Computer Organization