2017
GATE PI 20172016
GATE PI 20162015
GATE PI 20152014
GATE PI 20142013
GATE PI 20132012
GATE PI 20122011
GATE PI 20112010
GATE PI 20102009
GATE PI 20092008
GATE PI 20082007
GATE PI 20072006
GATE PI 20062005
GATE PI 20052004
GATE PI 20042003
GATE PI 20032002
GATE PI 20022001
GATE PI 20011995
GATE PI 19951994
GATE PI 19941993
GATE PI 19931992
GATE PI 19921991
GATE PI 19911990
GATE PI 19901989
GATE PI 1989GATE PI 2012
Paper was held on Thu, Jan 1, 1970 12:00 AM
1
A mold having dimensions $$100 \times 90 \times 20$$ (all in $$mm$$) is filled with molten metal througgh a gate with height $$'h'$$ and $$C.S$$ area $$A,$$ the mould filling time is $${t_1}$$. The height is now quadrupled and the cross sectional area is halved. The corresponding filling time is $${t_2}$$. The ratio $${t_2}/{t_1}$$ is
2
The inverse Laplace transform of the function $$F\left( s \right) = {1 \over {s\left( {s + 1} \right)}}$$ is given by
3
For the matrix $$A = \left[ {\matrix{
5 & 3 \cr
1 & 3 \cr
} } \right],$$ ONE of the normalized eigen vectors is given as
4
Consider the differential equation $$\,\,{x^2}{{{d^2}y} \over {d{x^2}}} + x{{dy} \over {dx}} - 4y = 0\,\,\,$$ with the boundary conditions of $$\,\,y\left( 0 \right) = 0\,\,\,$$ and $$\,\,y\left( 1 \right) = 1.\,\,\,$$ The complete solution of the differential equation is
5
An automobile plant contracted to buy shock absorbers from two suppliers $$X$$ and $$Y$$. $$X$$ supplies $$60$$% and $$Y$$ supplies $$40$$% of the shock absorbers. All shock absorbers are subjected to a quality test. The ones that pass the quality test are considered reliable. Of $$X'$$ s shock absorbers, $$96$$% are reliable. Of $$Y'$$ s shock absorbers, $$72$$% are reliable. The probability that a randomly choosen shock absorber, which is found to reliable, is made by $$Y$$ is
6
A box contains $$4$$ red balls and $$6$$ black balls. Three balls are selected randomly from the box one after another, without replacement. The probability that the selected set contains one red ball and two black balls is
7
For the spherical surface $${x^2} + {y^2} + {z^2} = 1,$$ the unit outward normal vector at the point $$\left( {{1 \over {\sqrt 2 }},{1 \over {\sqrt 2 }},0} \right)$$ is given by
8
A political party orders an arch for the entrance to the ground in which the annual convention is being held. The profile of the arch follows the equation $$y = 2x\,\,\, - 0.1{x^2}$$ where $$y$$ is the height of the arch in meters. The maximum possible height of the arch is
9
At $$x=0,$$ the function $$f\left( x \right) = {x^3} + 1$$ has
10
$$\,\mathop {Lim}\limits_{x \to 0} \left( {{{1 - \cos x} \over {{x^2}}}} \right)$$ is
11
Consider the function $$f\left( x \right) = \left| x \right|$$ in the interval $$\,\, - 1 \le x \le 1.\,\,\,$$ At the point $$x=0, f(x)$$ is
12
The area enclosed between the straight line $$y=x$$ and the parabola $$y = {x^2}$$ in the $$x-y$$ plane is
13
$$x+2y+z=4, 2x+y+2z=5, x-y+z=1$$
The system of algebraic equations given above has
The system of algebraic equations given above has
14
Consider two infinitely long thin concentric tubes of circular cross section as shown in the figure. If $${D_1}$$ and $${D_2}$$ are the diameters of the inner and outer tubes respectively, then the view factor $${F_{22}}$$ is given by
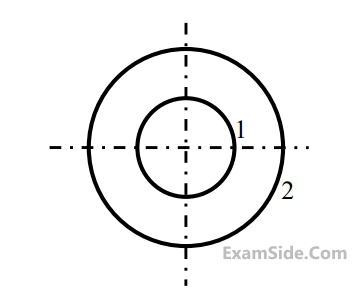

15
For an opaque surface, the absorptivity $$\left( \alpha \right),$$ transmissivity $$\left( \tau \right)$$ and reflectivity $$\left( \rho \right)$$ are related by the equation:
16
Which one of the following configurations has the highest fin effectiveness?
17
In a $$DC$$ $$arc$$ welding operating, the length characteristic was obtained as $${V_{arc}} = 20 + 5l$$ where the $$arc$$ length $$l$$ was varied between $$5mm$$ and $$7mm.$$ Here $${V_{arc}}$$ denotes the arc voltage in volts. The $$arc$$ current was varied from $$400A$$ to $$500A.$$ Assuming linear power source characteristic, the open circuit voltage and the short circuit current for the welding operation are
18
A $$CNC$$ vertical milling machine has to cut a straight slot of $$10$$ $$mm$$ width and $$2$$ $$mm$$ depth by a cutter of $$10$$ $$mm$$ diameter between points $$(0, 0)$$ and $$(100, 100)$$ on the $$XY$$ plane (dimensions in $$mm$$). The feed rate used for milling is $$50$$ $$mm/min.$$ Milling time for the slot (in seconds) is
19
In a single pass drilling operation, a through hole of $$15$$ $$mm$$ diameter is to be drilled in a steel plate of $$50mm$$ thickness. Drill spindle speed is $$500epm,$$ feed is $$0.2mm/rev$$ and drill point angle is $${118^ \circ }.$$ Assuming $$2mm$$ clearance at approach and exit, the total drill time (in seconds) is
20
In a shaping process, the number of double strokes per minute is $$30$$ and the quick return ratio is $$0.6,$$ If the length of the stroke is $$250mm,$$ the average cutting velocity in $$m/min$$ is
21
Calculate the punch size in $$mm,$$ for a circular blanking operation for which details are given below.
Size of the blank $$25$$ $$mm$$
Thickness of the sheet $$2$$ $$mm$$
Radial clearance between punch and die $$0.06$$ $$mm,$$ Die allowance $$0.05$$ $$mm$$
22
Match the following metal forming processes with their associated stresses in the Work-piece


23
In a single pass rolling process using $$410mm$$ diameter steel rollers, a strip of width $$140mm$$ and thickness $$8mm$$ undergoes $$10\% $$ reduction of thickness. The angle of bite in radians is
24
A solid cylinder of diameter $$100$$ $$mm$$ and height $$50$$ $$mm$$ is forged between two frictionless flat dies to a height of $$25$$ $$mm.$$ The percentage change in diameter is
25
A Sine bar has a length of $$250mm.$$ Each roller has a diameter of $$20mm.$$ During taper angle measurement of a component, the height from the surface plate to the center of a roller is $$100mm.$$ The calculated taper angle (in degrees) is
26
In an interchangeable assembly, shafts of size $${25.000^{\matrix{
{ + 0.040} \cr
{ - 0.010} \cr
} }}\,\,mm$$ mate with holes of size $${25.000^{\matrix{
{ + 0.030} \cr
{ + 0.020} \cr
} }}\,\,mm.$$
The maximum interference (in microns) in the assembly is