1
GATE ME 2017 Set 1
Numerical
+2
-0
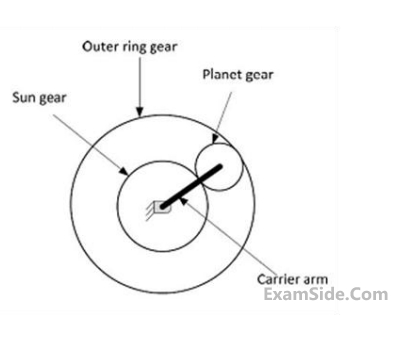
In an epicyclic gear train, shown in the figure, the outer ring gear is fixed, while the sun gear rotates counterclockwise at 100 rpm. Let the number of teeth on the sun, planet and outer gears to be 50, 25 and 100, respectively. The ratio of magnitudes of angular velocity of the planet gear to the angular velocity of the carrier arm is _________.

Your input ____
2
GATE ME 2016 Set 1
MCQ (Single Correct Answer)
+2
-0.6
In the gear train shown, gear 3 is carried on arm 5. Gear 3 meshes with gear 2 and gear 4. The number of teeth on gear 2, 3, and 4 are 60, 20, and 100, respectively. If gear 2 is fixed and gear rotates with an angular velocity of 100 rpm in the counterclockwise direction, the angular speed of arm 5 (in rpm) is


3
GATE ME 2015 Set 1
MCQ (Single Correct Answer)
+2
-0.6
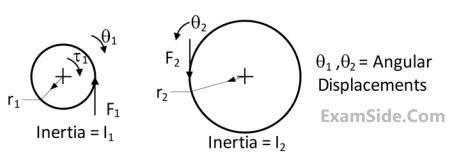
A pinion with radius $${r_1}$$, and inertia $${{\rm I}_1}$$ is driving a gear with radius $${r_2}$$ and inertia $${{\rm I}_2}$$ . Torque $${\tau _1}$$ is applied on pinion. The following are free body diagrams of pinion and gear showing important forces ($${F_1}$$and $${F_2}$$) of interaction. Which of the following relations hold true?

4
GATE ME 2014
MCQ (Single Correct Answer)
+2
-0.6
It is desired to avoid interference in a pair of spur gears having a 20o pressure angle. With increase in pinion to gear speed ratio, the minimum number of teeth on the pinion
GATE ME Subjects
Engineering Mechanics
Machine Design
Strength of Materials
Heat Transfer
Production Engineering
Industrial Engineering
Turbo Machinery
Theory of Machines
Engineering Mathematics
Fluid Mechanics
Thermodynamics
General Aptitude