2025
JEE Main 2025 (Online) 8th April Evening ShiftJEE Main 2025 (Online) 7th April Evening ShiftJEE Main 2025 (Online) 7th April Morning ShiftJEE Main 2025 (Online) 4th April Evening ShiftJEE Main 2025 (Online) 4th April Morning ShiftJEE Main 2025 (Online) 3rd April Evening ShiftJEE Main 2025 (Online) 3rd April Morning ShiftJEE Main 2025 (Online) 2nd April Evening ShiftJEE Main 2025 (Online) 2nd April Morning ShiftJEE Main 2025 (Online) 29th January Evening ShiftJEE Main 2025 (Online) 29th January Morning ShiftJEE Main 2025 (Online) 28th January Evening ShiftJEE Main 2025 (Online) 28th January Morning ShiftJEE Main 2025 (Online) 24th January Evening ShiftJEE Main 2025 (Online) 24th January Morning ShiftJEE Main 2025 (Online) 23rd January Evening ShiftJEE Main 2025 (Online) 23rd January Morning ShiftJEE Main 2025 (Online) 22nd January Evening ShiftJEE Main 2025 (Online) 22nd January Morning Shift2024
JEE Main 2024 (Online) 9th April Evening ShiftJEE Main 2024 (Online) 9th April Morning ShiftJEE Main 2024 (Online) 8th April Evening ShiftJEE Main 2024 (Online) 8th April Morning ShiftJEE Main 2024 (Online) 6th April Evening ShiftJEE Main 2024 (Online) 6th April Morning ShiftJEE Main 2024 (Online) 5th April Evening ShiftJEE Main 2024 (Online) 5th April Morning ShiftJEE Main 2024 (Online) 4th April Evening ShiftJEE Main 2024 (Online) 4th April Morning ShiftJEE Main 2024 (Online) 1st February Evening ShiftJEE Main 2024 (Online) 1st February Morning ShiftJEE Main 2024 (Online) 31st January Evening ShiftJEE Main 2024 (Online) 31st January Morning ShiftJEE Main 2024 (Online) 30th January Evening ShiftJEE Main 2024 (Online) 30th January Morning ShiftJEE Main 2024 (Online) 29th January Evening ShiftJEE Main 2024 (Online) 29th January Morning ShiftJEE Main 2024 (Online) 27th January Evening ShiftJEE Main 2024 (Online) 27th January Morning Shift2023
JEE Main 2023 (Online) 15th April Morning ShiftJEE Main 2023 (Online) 13th April Evening ShiftJEE Main 2023 (Online) 13th April Morning ShiftJEE Main 2023 (Online) 12th April Morning ShiftJEE Main 2023 (Online) 11th April Evening ShiftJEE Main 2023 (Online) 11th April Morning ShiftJEE Main 2023 (Online) 10th April Evening ShiftJEE Main 2023 (Online) 10th April Morning ShiftJEE Main 2023 (Online) 8th April Evening ShiftJEE Main 2023 (Online) 8th April Morning ShiftJEE Main 2023 (Online) 6th April Evening ShiftJEE Main 2023 (Online) 6th April Morning ShiftJEE Main 2023 (Online) 1st February Evening ShiftJEE Main 2023 (Online) 1st February Morning ShiftJEE Main 2023 (Online) 31st January Evening ShiftJEE Main 2023 (Online) 31st January Morning ShiftJEE Main 2023 (Online) 30th January Evening ShiftJEE Main 2023 (Online) 30th January Morning ShiftJEE Main 2023 (Online) 29th January Evening ShiftJEE Main 2023 (Online) 29th January Morning ShiftJEE Main 2023 (Online) 25th January Evening ShiftJEE Main 2023 (Online) 25th January Morning ShiftJEE Main 2023 (Online) 24th January Evening ShiftJEE Main 2023 (Online) 24th January Morning Shift2022
JEE Main 2022 (Online) 29th July Evening ShiftJEE Main 2022 (Online) 29th July Morning ShiftJEE Main 2022 (Online) 28th July Evening ShiftJEE Main 2022 (Online) 28th July Morning ShiftJEE Main 2022 (Online) 27th July Evening ShiftJEE Main 2022 (Online) 27th July Morning ShiftJEE Main 2022 (Online) 26th July Evening ShiftJEE Main 2022 (Online) 26th July Morning ShiftJEE Main 2022 (Online) 25th July Evening ShiftJEE Main 2022 (Online) 25th July Morning ShiftJEE Main 2022 (Online) 30th June Morning ShiftJEE Main 2022 (Online) 29th June Evening ShiftJEE Main 2022 (Online) 29th June Morning ShiftJEE Main 2022 (Online) 28th June Evening ShiftJEE Main 2022 (Online) 28th June Morning ShiftJEE Main 2022 (Online) 27th June Evening ShiftJEE Main 2022 (Online) 27th June Morning ShiftJEE Main 2022 (Online) 26th June Evening ShiftJEE Main 2022 (Online) 26th June Morning ShiftJEE Main 2022 (Online) 25th June Evening ShiftJEE Main 2022 (Online) 25th June Morning ShiftJEE Main 2022 (Online) 24th June Evening ShiftJEE Main 2022 (Online) 24th June Morning Shift2021
JEE Main 2021 (Online) 1st September Evening ShiftJEE Main 2021 (Online) 31st August Evening ShiftJEE Main 2021 (Online) 31st August Morning ShiftJEE Main 2021 (Online) 27th August Evening ShiftJEE Main 2021 (Online) 27th August Morning ShiftJEE Main 2021 (Online) 26th August Evening ShiftJEE Main 2021 (Online) 26th August Morning ShiftJEE Main 2021 (Online) 27th July Evening ShiftJEE Main 2021 (Online) 27th July Morning ShiftJEE Main 2021 (Online) 25th July Evening ShiftJEE Main 2021 (Online) 25th July Morning ShiftJEE Main 2021 (Online) 22th July Evening ShiftJEE Main 2021 (Online) 20th July Evening ShiftJEE Main 2021 (Online) 20th July Morning ShiftJEE Main 2021 (Online) 18th March Evening ShiftJEE Main 2021 (Online) 18th March Morning ShiftJEE Main 2021 (Online) 17th March Evening ShiftJEE Main 2021 (Online) 17th March Morning ShiftJEE Main 2021 (Online) 16th March Evening ShiftJEE Main 2021 (Online) 16th March Morning ShiftJEE Main 2021 (Online) 26th February Evening ShiftJEE Main 2021 (Online) 26th February Morning ShiftJEE Main 2021 (Online) 25th February Evening ShiftJEE Main 2021 (Online) 25th February Morning ShiftJEE Main 2021 (Online) 24th February Evening ShiftJEE Main 2021 (Online) 24th February Morning Shift2020
JEE Main 2020 (Online) 6th September Evening SlotJEE Main 2020 (Online) 6th September Morning SlotJEE Main 2020 (Online) 5th September Evening SlotJEE Main 2020 (Online) 5th September Morning SlotJEE Main 2020 (Online) 4th September Evening SlotJEE Main 2020 (Online) 4th September Morning SlotJEE Main 2020 (Online) 3rd September Evening SlotJEE Main 2020 (Online) 3rd September Morning SlotJEE Main 2020 (Online) 2nd September Evening SlotJEE Main 2020 (Online) 2nd September Morning SlotJEE Main 2020 (Online) 9th January Evening SlotJEE Main 2020 (Online) 9th January Morning SlotJEE Main 2020 (Online) 8th January Evening SlotJEE Main 2020 (Online) 8th January Morning SlotJEE Main 2020 (Online) 7th January Evening SlotJEE Main 2020 (Online) 7th January Morning Slot2019
JEE Main 2019 (Online) 12th April Evening SlotJEE Main 2019 (Online) 12th April Morning SlotJEE Main 2019 (Online) 10th April Evening SlotJEE Main 2019 (Online) 10th April Morning SlotJEE Main 2019 (Online) 9th April Evening SlotJEE Main 2019 (Online) 9th April Morning SlotJEE Main 2019 (Online) 8th April Evening SlotJEE Main 2019 (Online) 8th April Morning SlotJEE Main 2019 (Online) 12th January Evening SlotJEE Main 2019 (Online) 12th January Morning SlotJEE Main 2019 (Online) 11th January Evening SlotJEE Main 2019 (Online) 11th January Morning SlotJEE Main 2019 (Online) 10th January Evening SlotJEE Main 2019 (Online) 10th January Morning SlotJEE Main 2019 (Online) 9th January Evening SlotJEE Main 2019 (Online) 9th January Morning Slot2018
JEE Main 2018 (Online) 16th April Morning SlotJEE Main 2018 (Offline)JEE Main 2018 (Online) 15th April Evening SlotJEE Main 2018 (Online) 15th April Morning Slot2017
JEE Main 2017 (Online) 9th April Morning SlotJEE Main 2017 (Online) 8th April Morning SlotJEE Main 2017 (Offline)2016
JEE Main 2016 (Online) 10th April Morning SlotJEE Main 2016 (Online) 9th April Morning SlotJEE Main 2016 (Offline)2015
JEE Main 2015 (Offline)2014
JEE Main 2014 (Offline)2013
JEE Main 2013 (Offline)2012
AIEEE 20122011
AIEEE 20112010
AIEEE 20102009
AIEEE 20092008
AIEEE 20082007
AIEEE 20072006
AIEEE 20062005
AIEEE 20052004
AIEEE 20042003
AIEEE 20032002
AIEEE 2002JEE Main 2021 (Online) 31st August Evening Shift
Paper was held on Tue, Aug 31, 2021 9:30 AM
Chemistry
1
Arrange the following conformational isomers of n-butane in order of their increasing potential energy :
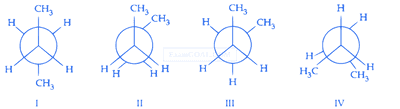

2
The Eu2+ ion is a strong reducing agent in spite of its ground state electronic configuration (outermost) : [Atomic number of Eu = 63]
3
The structures A and B formed in the following reaction are : [Ph = $$-$$C6H5]
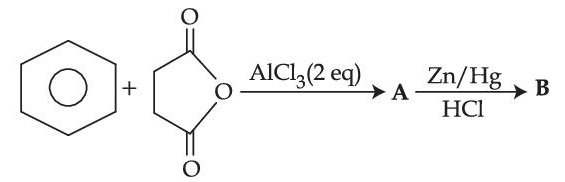

4
In which one of the following sets all species show disproportionation reaction?
5
Match List - I with List - II
Choose the most appropriate answer from the options given below :
| List - I (Parmeter) |
List - II (Unit) |
||
|---|---|---|---|
| (a) | Cell constant | (i) | $$S\,c{m^2}mo{l^{ - 1}}$$ |
| (b) | Molar conductivity | (ii) | Dimensionless |
| (c) | Conductivity | (iii) | $${m^{ - 1}}$$ |
| (d) | Degree of dissociation of electrolyte | (iv) | $${\Omega ^{ - 1}}{m^{ - 1}}$$ |
Choose the most appropriate answer from the options given below :
6
The major products A and B formed in the following reaction sequence are :
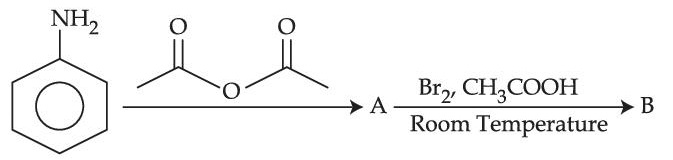

7
Which of the following is not an example of fibrous protein?
8
For the reaction given below :-
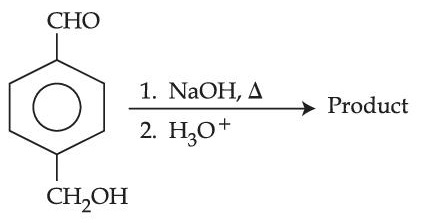
The compound which is not formed as a product in the reaction is a :

The compound which is not formed as a product in the reaction is a :
9
Spin only magnetic moment in BM of [Fe(CO)4(C2O4)]+ is :
10
The incorrect expression among the following is :
11
Match List - I with List - II :
Choose the most appropriate answer from the options given below :
| List - I (Metal Ion) |
List - II (Group of Qualitative analysis) |
||
|---|---|---|---|
| (a) | $$M{n^{2 + }}$$ | (i) | Group - III |
| (b) | $$A{s^{3 + }}$$ | (ii) | Group - IIA |
| (c) | $$C{u^{2 + }}$$ | (iii) | Group - IV |
| (d) | $$A{l^{3 + }}$$ | (iv) | Group - IIB |
Choose the most appropriate answer from the options given below :
12
The major product of the following reaction is :


13
For the following sequence of reactions, the correct
products are :
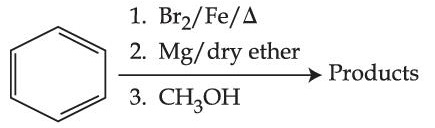
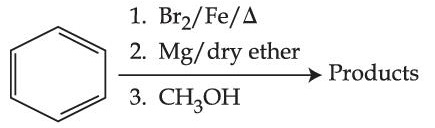
14
Identify correct A, B and C in the reaction sequence given below :


15
1.22 g of an organic acid is separately dissolved in 100 g of benzene (Kb = 2.6 K kg mol$$-$$1) and 100 g of acetone (Kb = 1.7 K kg mol$$-$$1). The acid is known to dimerize in benzene but remain as a monomer in acetone. The boiling point of the solution in acetone increases by 0.17$$^\circ$$C. The increase in boiling point of solution in benzene in $$^\circ$$C is x $$\times$$ 10$$-$$2. The value of x is ______________. (Nearest integer) [Atomic mass : C = 12.0, H = 1.0, O =16.0]
16
The value of magnetic quantum number of the outermost electron of Zn+ ion is ______________.
17
The pH of a solution obtained by mixing 50 mL of 1 M HCl and 30 mL of 1 M NaOH is x $$\times$$ 10$$-$$4. The value of x is ____________. (Nearest integer) [log 2.5 = 0.3979]
18
For the reaction A $$\to$$ B, the rate constant k(in s$$-$$1) is given by
$${\log _{10}}k = 20.35 - {{(2.47 \times {{10}^3})} \over T}$$
The energy of activation in kJ mol$$-$$1 is ____________. (Nearest integer) [Given : R = 8.314 J K$$-$$1 mol$$-$$1]
$${\log _{10}}k = 20.35 - {{(2.47 \times {{10}^3})} \over T}$$
The energy of activation in kJ mol$$-$$1 is ____________. (Nearest integer) [Given : R = 8.314 J K$$-$$1 mol$$-$$1]
19
Sodium oxide reacts with water to produce sodium hydroxide. 20.0 g of sodium oxide is dissolved in 500 mL of water. Neglecting the change in volume, the concentration of the resulting NaOH solution is ______________ $$\times$$ 10$$-$$1 M. (Nearest integer) [Atomic mass : Na = 23.0, O = 16.0, H = 1.0]
20
According to molecular orbital theory, the number of unpaired electron(s) in $$O_2^{2 - }$$ is :
21
The transformation occurring in Duma's method is given below :
$${C_2}{H_7}N + \left( {2x + {y \over 2}} \right)CuO \to xC{O_2} + {y \over 2}{H_2}O + {z \over 2}{N_2} + \left( {2x + {y \over 2}} \right)Cu$$
The value of y is ______________. (Integer answer)
$${C_2}{H_7}N + \left( {2x + {y \over 2}} \right)CuO \to xC{O_2} + {y \over 2}{H_2}O + {z \over 2}{N_2} + \left( {2x + {y \over 2}} \right)Cu$$
The value of y is ______________. (Integer answer)
Mathematics
1
If $$\alpha$$ + $$\beta$$ + $$\gamma$$ = 2$$\pi$$, then the system of equations
x + (cos $$\gamma$$)y + (cos $$\beta$$)z = 0
(cos $$\gamma$$)x + y + (cos $$\alpha$$)z = 0
(cos $$\beta$$)x + (cos $$\alpha$$)y + z = 0
has :
x + (cos $$\gamma$$)y + (cos $$\beta$$)z = 0
(cos $$\gamma$$)x + y + (cos $$\alpha$$)z = 0
(cos $$\beta$$)x + (cos $$\alpha$$)y + z = 0
has :
2
The domain of the function
$$f(x) = {\sin ^{ - 1}}\left( {{{3{x^2} + x - 1} \over {{{(x - 1)}^2}}}} \right) + {\cos ^{ - 1}}\left( {{{x - 1} \over {x + 1}}} \right)$$ is :
$$f(x) = {\sin ^{ - 1}}\left( {{{3{x^2} + x - 1} \over {{{(x - 1)}^2}}}} \right) + {\cos ^{ - 1}}\left( {{{x - 1} \over {x + 1}}} \right)$$ is :
3
Let S = {1, 2, 3, 4, 5, 6}. Then the probability that a randomly chosen onto function g from S to S satisfies g(3) = 2g(1) is :
4
Let f : N $$\to$$ N be a function such that f(m + n) = f(m) + f(n) for every m, n$$\in$$N. If f(6) = 18, then f(2) . f(3) is equal to :
5
If $$\alpha = \mathop {\lim }\limits_{x \to {\pi \over 4}} {{{{\tan }^3}x - \tan x} \over {\cos \left( {x + {\pi \over 4}} \right)}}$$ and $$\beta = \mathop {\lim }\limits_{x \to 0 } {(\cos x)^{\cot x}}$$ are the roots of the equation, ax2 + bx $$-$$ 4 = 0, then the ordered pair (a, b) is :
6
The locus of mid-points of the line segments joining ($$-$$3, $$-$$5) and the points on the ellipse $${{{x^2}} \over 4} + {{{y^2}} \over 9} = 1$$ is :
7
If $${{dy} \over {dx}} = {{{2^x}y + {2^y}{{.2}^x}} \over {{2^x} + {2^{x + y}}{{\log }_e}2}}$$, y(0) = 0, then for y = 1, the value of x lies in the interval :
8
If $$y{{dy} \over {dx}} = x\left[ {{{{y^2}} \over {{x^2}}} + {{\phi \left( {{{{y^2}} \over {{x^2}}}} \right)} \over {\phi '\left( {{{{y^2}} \over {{x^2}}}} \right)}}} \right]$$, x > 0, $$\phi$$ > 0, and y(1) = $$-$$1, then $$\phi \left( {{{{y^2}} \over 4}} \right)$$ is equal to :
9
The sum of the roots of the equation
$$x + 1 - 2{\log _2}(3 + {2^x}) + 2{\log _4}(10 - {2^{ - x}}) = 0$$, is :
$$x + 1 - 2{\log _2}(3 + {2^x}) + 2{\log _4}(10 - {2^{ - x}}) = 0$$, is :
10
If z is a complex number such that $${{z - i} \over {z - 1}}$$ is purely imaginary, then the minimum value of | z $$-$$ (3 + 3i) | is :
11
Let a1, a2, a3, ..... be an A.P. If $${{{a_1} + {a_2} + .... + {a_{10}}} \over {{a_1} + {a_2} + .... + {a_p}}} = {{100} \over {{p^2}}}$$, p $$\ne$$ 10, then $${{{a_{11}}} \over {{a_{10}}}}$$ is equal to :
12
Let A be the set of all points ($$\alpha$$, $$\beta$$) such that the area of triangle formed by the points (5, 6), (3, 2) and ($$\alpha$$, $$\beta$$) is 12 square units. Then the least possible length of a line segment joining the origin to a point in A, is :
13
Let f be any continuous function on [0, 2] and twice differentiable on (0, 2). If f(0) = 0, f(1) = 1 and f(2) = 2, then
14
If [x] is the greatest integer $$\le$$ x, then
$${\pi ^2}\int\limits_0^2 {\left( {\sin {{\pi x} \over 2}} \right)(x - [x]} {)^{[x]}}dx$$ is equal to :
$${\pi ^2}\int\limits_0^2 {\left( {\sin {{\pi x} \over 2}} \right)(x - [x]} {)^{[x]}}dx$$ is equal to :
15
The mean and variance of 7 observations are 8 and 16 respectively. If two observations are 6 and 8, then the variance of the remaining 5 observations is :
16
If the coefficient of a7b8 in the expansion of (a + 2b + 4ab)10 is K.216, then K is equal to _____________.
17
The number of 4-digit numbers which are neither multiple of 7 nor multiple of 3 is ____________.
18
If $$\int {{{\sin x} \over {{{\sin }^3}x + {{\cos }^3}x}}dx = } $$
$$\alpha {\log _e}|1 + \tan x| + \beta {\log _e}|1 - \tan x + {\tan ^2}x| + \gamma {\tan ^{ - 1}}\left( {{{2\tan x - 1} \over {\sqrt 3 }}} \right) + C$$, when C is constant of integration, then the value of $$18(\alpha + \beta + {\gamma ^2})$$ is ______________.
$$\alpha {\log _e}|1 + \tan x| + \beta {\log _e}|1 - \tan x + {\tan ^2}x| + \gamma {\tan ^{ - 1}}\left( {{{2\tan x - 1} \over {\sqrt 3 }}} \right) + C$$, when C is constant of integration, then the value of $$18(\alpha + \beta + {\gamma ^2})$$ is ______________.
19
The number of elements in the set $$\left\{ {A = \left( {\matrix{
a & b \cr
0 & d \cr
} } \right):a,b,d \in \{ - 1,0,1\} \,and\,{{(I - A)}^3} = I - {A^3}} \right\}$$, where I is 2 $$\times$$ 2 identity matrix, is :
20
If the line y = mx bisects the area enclosed by the lines x = 0, y = 0, x = $${3 \over 2}$$ and the curve y = 1 + 4x $$-$$ x2, then 12 m is equal to _____________.
21
Let f(x) be a cubic polynomial with f(1) = $$-$$10, f($$-$$1) = 6, and has a local minima at x = 1, and f'(x) has a local minima at x = $$-$$1. Then f(3) is equal to ____________.
Physics
1
Four identical hollow cylindrical columns of mild steel support a big structure of mass 50 $$\times$$ 103 kg. The inner and outer radii of each column are 50 cm and 100 cm respectively. Assuming uniform local distribution, calculate the compression strain of each column. [Use Y = 2.0 $$\times$$ 1011 Pa, g = 9.8 m/s2]
2
A current of 1.5 A is flowing through a triangle, of side 9 cm each. The magnetic field at the centroid of the triangle is :
(Assume that the current is flowing in the clockwise direction.)
(Assume that the current is flowing in the clockwise direction.)
3
A system consists of two identical spheres each of mass 1.5 kg and radius 50 cm at the end of light rod. The distance between the centres of the two spheres is 5 m. What will be the moment of inertia of the system about an axis perpendicular to the rod passing through its midpoint?
4
Statement I :
Two forces $$\left( {\overrightarrow P + \overrightarrow Q } \right)$$ and $$\left( {\overrightarrow P - \overrightarrow Q } \right)$$ where $$\overrightarrow P \bot \overrightarrow Q $$, when act at an angle $$\theta$$1 to each other, the magnitude of their resultant is $$\sqrt {3({P^2} + {Q^2})} $$, when they act at an angle $$\theta$$2, the magnitude of their resultant becomes $$\sqrt {2({P^2} + {Q^2})} $$. This is possible only when $${\theta _1} < {\theta _2}$$.
Statement II :
In the situation given above.
$$\theta$$1 = 60$$^\circ$$ and $$\theta$$2 = 90$$^\circ$$
In the light of the above statements, choose the most appropriate answer from the options given below :-
Two forces $$\left( {\overrightarrow P + \overrightarrow Q } \right)$$ and $$\left( {\overrightarrow P - \overrightarrow Q } \right)$$ where $$\overrightarrow P \bot \overrightarrow Q $$, when act at an angle $$\theta$$1 to each other, the magnitude of their resultant is $$\sqrt {3({P^2} + {Q^2})} $$, when they act at an angle $$\theta$$2, the magnitude of their resultant becomes $$\sqrt {2({P^2} + {Q^2})} $$. This is possible only when $${\theta _1} < {\theta _2}$$.
Statement II :
In the situation given above.
$$\theta$$1 = 60$$^\circ$$ and $$\theta$$2 = 90$$^\circ$$
In the light of the above statements, choose the most appropriate answer from the options given below :-
5
A free electron of 2.6 eV energy collides with a H+ ion. This results in the formation of a hydrogen atom in the first excited state and a photon is released. Find the frequency of the emitted photon. (h = 6.6 $$\times$$ 10$$-$$34 Js)
6
Two thin metallic spherical shells of radii r1 and r2 (r1 < r2) are placed with their centres coinciding. A material of thermal conductivity K is filled in the space between the shells. The inner shell is maintained at temperature $$\theta$$1 and the outer shell at temperature $$\theta$$2($$\theta$$1 < $$\theta$$2). The rate at which heat flows radially through the material is :-
7
If VA and VB are the input voltages (either 5V or 0V) and V0 is the output voltage then the two gates represented in the following circuit (A) and (B) are :-

8
Consider two separate ideal gases of electrons and protons having same number of particles. The temperature of both the gases are same. The ratio of the uncertainty in determining the position of an electron to that of a proton is proportional to :-
9
A bob of mass 'm' suspended by a thread of length l undergoes simple harmonic oscillations with time period T. If the bob is immersed in a liquid that has density $${1 \over 4}$$ times that of the bob and the length of the thread is increased by 1/3rd of the original length, then the time period of the simple harmonic oscillations will be :-
10
Statement : 1
If three forces $${\overrightarrow F _1},{\overrightarrow F _2}$$ and $${\overrightarrow F _3}$$ are represented by three sides of a triangle and $${\overrightarrow F _1} + {\overrightarrow F _2} = - {\overrightarrow F _3}$$, then these three forces are concurrent forces and satisfy the condition for equilibrium.
Statement : 2
A triangle made up of three forces $${\overrightarrow F _1}$$, $${\overrightarrow F _2}$$ and $${\overrightarrow F _3}$$ as its sides taken in the same order, satisfy the condition for translatory equilibrium.
In the light of the above statements, choose the most appropriate answer from the options given below :
If three forces $${\overrightarrow F _1},{\overrightarrow F _2}$$ and $${\overrightarrow F _3}$$ are represented by three sides of a triangle and $${\overrightarrow F _1} + {\overrightarrow F _2} = - {\overrightarrow F _3}$$, then these three forces are concurrent forces and satisfy the condition for equilibrium.
Statement : 2
A triangle made up of three forces $${\overrightarrow F _1}$$, $${\overrightarrow F _2}$$ and $${\overrightarrow F _3}$$ as its sides taken in the same order, satisfy the condition for translatory equilibrium.
In the light of the above statements, choose the most appropriate answer from the options given below :
11
If velocity [V], time [T] and force [F] are chosen as the base quantities, the dimensions of the mass will be :
12
The magnetic field vector of an electromagnetic wave is given by $$B = {B_0}{{\widehat i + \widehat j} \over {\sqrt 2 }}\cos (kz - \omega t)$$; where $$\widehat i,\widehat j$$ represents unit vector along x and y-axis respectively. At t = 0s, two electric charges q1 of 4$$\pi$$ coulomb and q2 of 2$$\pi$$ coulomb located at $$\left( {0,0,{\pi \over k}} \right)$$ and $$\left( {0,0,{{3\pi } \over k}} \right)$$, respectively, have the same velocity of 0.5 c $$\widehat i$$, (where c is the velocity of light). The ratio of the force acting on charge q1 to q2 is :-
13
The equivalent resistance of the given circuit between the terminals A and B is :
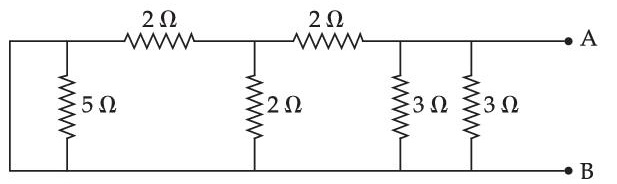

14
Choose the incorrect statement :
(1) The electric lines of force entering into a Gaussian surface provide negative flux.
(2) A charge 'q' is placed at the centre of a cube. The flux through all the faces will be the same.
(3) In a uniform electric field net flux through a closed Gaussian surface containing no net charge, is zero.
(4) When electric field is parallel to a Gaussian surface, it provides a finite non-zero flux.
Choose the most appropriate answer from the options given below
(1) The electric lines of force entering into a Gaussian surface provide negative flux.
(2) A charge 'q' is placed at the centre of a cube. The flux through all the faces will be the same.
(3) In a uniform electric field net flux through a closed Gaussian surface containing no net charge, is zero.
(4) When electric field is parallel to a Gaussian surface, it provides a finite non-zero flux.
Choose the most appropriate answer from the options given below
15
A mixture of hydrogen and oxygen has volume 500 cm3, temperature 300 K, pressure 400 kPa and mass 0.76 g. The ratio of masses of oxygen to hydrogen will be :-
16
A block moving horizontally on a smooth surface with a speed of 40 m/s splits into two parts with masses in the ratio of 1 : 2. If the smaller part moves at 60 m/s in the same direction, then the fractional change in kinetic energy is :-
17
A coil is placed in a magnetic field $$\overrightarrow B $$ as shown below :
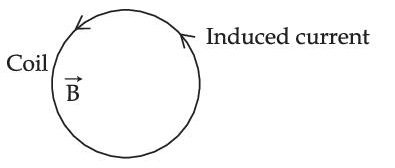
A current is induced in the coil because $$\overrightarrow B $$ is :

A current is induced in the coil because $$\overrightarrow B $$ is :
18
For a body executing S.H.M. :
(1) Potential energy is always equal to its K.E.
(2) Average potential and kinetic energy over any given time interval are always equal.
(3) Sum of the kinetic and potential energy at any point of time is constant.
(4) Average K.E. in one time period is equal to average potential energy in one time period.
Choose the most appropriate option from the options given below :
(1) Potential energy is always equal to its K.E.
(2) Average potential and kinetic energy over any given time interval are always equal.
(3) Sum of the kinetic and potential energy at any point of time is constant.
(4) Average K.E. in one time period is equal to average potential energy in one time period.
Choose the most appropriate option from the options given below :
19
Statement - I :
To get a steady dc output from the pulsating voltage received from a full wave rectifier we can connect a capacitor across the output parallel to the load RL.
Statement - II :
To get a steady dc output from the pulsating voltage received from a full wave rectifier we can connect an inductor in series with RL.
In the light of the above statements, choose the most appropriate answer from the options given below :
To get a steady dc output from the pulsating voltage received from a full wave rectifier we can connect a capacitor across the output parallel to the load RL.
Statement - II :
To get a steady dc output from the pulsating voltage received from a full wave rectifier we can connect an inductor in series with RL.
In the light of the above statements, choose the most appropriate answer from the options given below :
20
If RE be the radius of Earth, then the ratio between the acceleration due to gravity at a depth 'r' below and a height 'r' above the earth surface is : (Given : r < RE)
21
A parallel plate capacitor of capacitance 200 $$\mu$$F is connected to a battery of 200 V. A dielectric slab of dielectric constant 2 is now inserted into the space between plates of capacitor while the battery remain connected. The change in the electrostatic energy in the capacitor will be ____________J.
22
A long solenoid with 1000 turns/m has a core material with relative permeability 500 and volume 103 cm3. If the core material is replaced by another material having relative permeability of 750 with same volume maintaining same current of 0.75 A in the solenoid, the fractional change in the magnetic moment of the core would be approximately $$\left( {{x \over {499}}} \right)$$. Find the value of x.
23
A particle is moving with constant acceleration 'a'. Following graph shows v2 versus x(displacement) plot. The acceleration of the particle is ___________ m/s2.
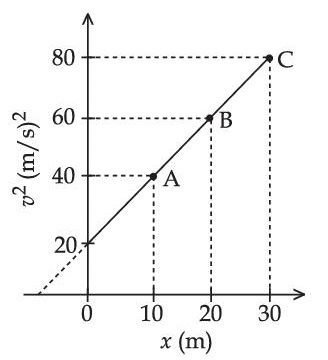

24
In a Young's double slit experiment, the slits are separated by 0.3 mm and the screen is 1.5 m away from the plane of slits. Distance between fourth bright fringes on both sides of central bright is 2.4 cm. The frequency of light used is ______________ $$\times$$ 1014 Hz.
25
The diameter of a spherical bob is measured using a vernier callipers. 9 divisions of the main scale, in the vernier callipers, are equal to 10 divisions of vernier scale. One main scale division is 1 mm. The main scale reading is 10 mm and 8th division of vernier scale was found to coincide exactly with one of the main scale division. If the given vernier callipers has positive zero error of 0.04 cm, then the radius of the bob is ___________ $$\times$$ 10$$-$$2 cm.
26
A sample of gas with $$\gamma$$ = 1.5 is taken through an adiabatic process in which the volume is compressed from 1200 cm3 to 300 cm3. If the initial pressure is 200 kPa. The absolute value of the workdone by the gas in the process = _____________ J.
27
At very high frequencies, the effective impendence of the given circuit will be ________________ $$\Omega$$.
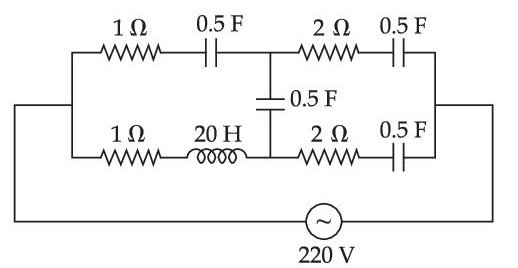

28
Cross-section view of a prism is the equilateral triangle ABC in the figure. The minimum deviation is observed using this prism when the angle of incidence is equal to the prism angle. The time taken by light to travel from P (midpoint of BC) to A is ______________ $$\times$$ 10$$-$$10 s. (Given, speed of light in vacuum = 3 $$\times$$ 108 m/s and cos30$$^\circ$$ = $${{\sqrt 3 } \over 2}$$)
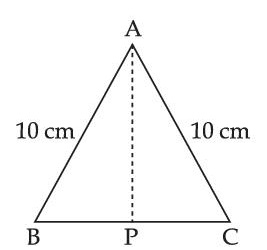

29
A resistor dissipates 192 J of energy in 1s when a current of 4A is passed through it. Now, when the current is doubled, the amount of thermal energy dissipated in 5s in _________ J.