Chemistry
1
Which one of the following compounds will give orange precipitate when treated with 2, 4-dinitrophenyl hydrazine?
2
The oxidation states of 'P' in H4P2O7, H4P2O5 and H4P2O6, respectively, are :
3
For a reaction of order n, the unit of the rate constant is :
4
Given below are two statements :
Statement I : Aniline is less basic than acetamide.
Statement II : In aniline, the lone pair of electrons on nitrogen atom is delocalized over benzene ring due to resonance and hence less available to a proton.
Choose the most appropriate option;
Statement I : Aniline is less basic than acetamide.
Statement II : In aniline, the lone pair of electrons on nitrogen atom is delocalized over benzene ring due to resonance and hence less available to a proton.
Choose the most appropriate option;
5
The type of hybridisation and magnetic property of the complex [MnCl6]3$$-$$, respectively, are :
6
The number of geometrical isomers found in the metal
complexes [PtCl2(NH3)2], [Ni(CO)4], [Ru(H2O)3Cl3 and [CoCl2(NH3)4]+ respectively, are :
complexes [PtCl2(NH3)2], [Ni(CO)4], [Ru(H2O)3Cl3 and [CoCl2(NH3)4]+ respectively, are :
7
Presence of which reagent will affect the reversibility of the following reaction, and change it to a irreversible reaction :
CH4 + I2 $$\mathrel{\mathop{\kern0pt\rightleftharpoons} \limits_{{\mathop{\rm Re}\nolimits} versible}^{hv}} $$ CH3 $$-$$ I + HI
CH4 + I2 $$\mathrel{\mathop{\kern0pt\rightleftharpoons} \limits_{{\mathop{\rm Re}\nolimits} versible}^{hv}} $$ CH3 $$-$$ I + HI
8
Which one among the following chemical tests is used to distinguish monosaccharide from disaccharide?
9
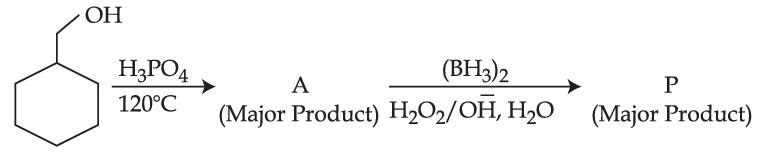
Consider the above reaction and identify the Product P :
10
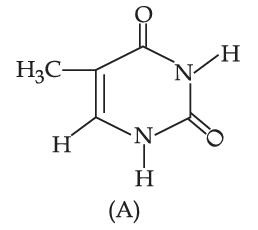
The compound 'A' is a complementary base of _______________ in DNA stands.
11
Staggered and eclipsed conformers of ethane are :
12
Match List - I with List - II :
Choose the most appropriate answer from the options given below
| List - I | List - II | ||
|---|---|---|---|
| (a) | NaOH | (i) | Acidic |
| (b) | $$Be{(OH)_2}$$ | (ii) | Basic |
| (c) | $$Ca{(OH)_2}$$ | (iii) | Amphoteric |
| (d) | $$B{(OH)_3}$$ | ||
| (e) | $$Al{(OH)_3}$$ |
Choose the most appropriate answer from the options given below
13
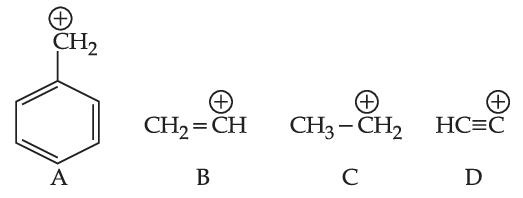
The correct order of stability of given carbocation is :
14
The density of NaOH solution is 1.2 g cm$$-$$3. The molality of this solution is _____________ m. (Round off to the Nearest Integer)
[Use : Atomic mass : Na : 23.0 u, O : 16.0 u, H : 1.0 u, Density of H2O : 1.0 g cm$$-$$3]
[Use : Atomic mass : Na : 23.0 u, O : 16.0 u, H : 1.0 u, Density of H2O : 1.0 g cm$$-$$3]
15
The conductivity of a weak acid HA of concentration 0.001 mol L$$-$$1 is 2.0 $$\times$$ 10$$-$$5 S cm$$-$$1. If $$\Lambda _m^o$$(HA) = 190 S cm2 mol$$-$$1, the ionization constant (Ka) of HA is equal to ______________ $$\times$$ 10$$-$$6. (Round off to the Nearest Integer)
16
1.46 g of a biopolymer dissolved in a 100 mL water at 300 K exerted an osmotic pressure of 2.42 $$\times$$ 10$$-$$3 bar.
The molar mass of the biopolymer is _____________ $$\times$$ 104 g mol$$-$$1. (Round off to the Nearest Integer)
[Use : R = 0.083 L bar mol$$-$$1 K$$-$$1]
The molar mass of the biopolymer is _____________ $$\times$$ 104 g mol$$-$$1. (Round off to the Nearest Integer)
[Use : R = 0.083 L bar mol$$-$$1 K$$-$$1]
17
An organic compound is subjected to chlorination to get compound A using 5.0 g of chlorine. When 0.5 g of compound A is reacted with AgNO3 [Carius Method], the percentage of chlorine in compound A is ____________ when it forms 0.3849 g of AgCl. (Round off to the Nearest Integer)
(Atomic masses of Ag and Cl are 107.87 and 35.5 respectively)
(Atomic masses of Ag and Cl are 107.87 and 35.5 respectively)
18
The number of geometrical isomers possible in triamminetrinitrocobalt (III) is X and in trioxalatochromate (III) is Y. Then the value of X + Y is _______________.
19
In gaseous triethyl amine the "$$-$$C$$-$$N$$-$$C$$-$$" bond angle is _________ degree.
20
For water at 100$$^\circ$$ C and 1 bar,
$$\Delta$$vap H $$-$$ $$\Delta$$vap U = _____________ $$\times$$ 102 J mol$$-$$1. (Round off to the Nearest Integer)
[Use : R = 8.31 J mol$$-$$1 K$$-$$1]
[Assume volume of H2O(l) is much smaller than volume of H2O(g). Assume H2O(g) treated as an ideal gas]
$$\Delta$$vap H $$-$$ $$\Delta$$vap U = _____________ $$\times$$ 102 J mol$$-$$1. (Round off to the Nearest Integer)
[Use : R = 8.31 J mol$$-$$1 K$$-$$1]
[Assume volume of H2O(l) is much smaller than volume of H2O(g). Assume H2O(g) treated as an ideal gas]
21
PCl5 $$\rightleftharpoons$$ PCl3 + Cl2
Kc = 1.844
3.0 moles of PCl5 is introduced in a 1 L closed reaction vessel at 380 K. The number of moles of PCl5 at equilibrium is ______________ $$\times$$ 10$$-$$3. (Round off to the Nearest Integer)
Kc = 1.844
3.0 moles of PCl5 is introduced in a 1 L closed reaction vessel at 380 K. The number of moles of PCl5 at equilibrium is ______________ $$\times$$ 10$$-$$3. (Round off to the Nearest Integer)
22
The difference between bond orders of CO and NO$$^ \oplus $$ is $${x \over 2}$$ where x = _____________. (Round off to the Nearest Integer)
Mathematics
1
If the mean and variance of the following data : 6, 10, 7, 13, a, 12, b, 12 are 9 and $${{37} \over 4}$$
respectively, then (a $$-$$ b)2 is equal to :
respectively, then (a $$-$$ b)2 is equal to :
2
Let $$\overrightarrow a = \widehat i + \widehat j + 2\widehat k$$ and $$\overrightarrow b = - \widehat i + 2\widehat j + 3\widehat k$$. Then the vector product $$\left( {\overrightarrow a + \overrightarrow b } \right) \times \left( {\left( {\overrightarrow a \times \left( {\left( {\overrightarrow a - \overrightarrow b } \right) \times \overrightarrow b } \right)} \right) \times \overrightarrow b } \right)$$ is equal to :
3
The value of the definite integral
$$\int\limits_{ - {\pi \over 4}}^{{\pi \over 4}} {{{dx} \over {(1 + {e^{x\cos x}})({{\sin }^4}x + {{\cos }^4}x)}}} $$ is equal to :
$$\int\limits_{ - {\pi \over 4}}^{{\pi \over 4}} {{{dx} \over {(1 + {e^{x\cos x}})({{\sin }^4}x + {{\cos }^4}x)}}} $$ is equal to :
4
Let C be the set of all complex numbers. Let
$${S_1} = \{ z \in C||z - 3 - 2i{|^2} = 8\} $$
$${S_2} = \{ z \in C|{\mathop{\rm Re}\nolimits} (z) \ge 5\} $$ and
$${S_3} = \{ z \in C||z - \overline z | \ge 8\} $$.
Then the number of elements in $${S_1} \cap {S_2} \cap {S_3}$$ is equal to :
$${S_1} = \{ z \in C||z - 3 - 2i{|^2} = 8\} $$
$${S_2} = \{ z \in C|{\mathop{\rm Re}\nolimits} (z) \ge 5\} $$ and
$${S_3} = \{ z \in C||z - \overline z | \ge 8\} $$.
Then the number of elements in $${S_1} \cap {S_2} \cap {S_3}$$ is equal to :
5
If the area of the bounded region
$$R = \left\{ {(x,y):\max \{ 0,{{\log }_e}x\} \le y \le {2^x},{1 \over 2} \le x \le 2} \right\}$$ is ,
$$\alpha {({\log _e}2)^{ - 1}} + \beta ({\log _e}2) + \gamma $$, then the value of $${(\alpha + \beta - 2\lambda )^2}$$ is equal to :
$$R = \left\{ {(x,y):\max \{ 0,{{\log }_e}x\} \le y \le {2^x},{1 \over 2} \le x \le 2} \right\}$$ is ,
$$\alpha {({\log _e}2)^{ - 1}} + \beta ({\log _e}2) + \gamma $$, then the value of $${(\alpha + \beta - 2\lambda )^2}$$ is equal to :
6
A ray of light through (2, 1) is reflected at a point P on the y-axis and then passes through the point (5, 3). If this reflected ray is the directrix of an ellipse with eccentricity $${1 \over 3}$$ and the distance of the nearer focus from this directrix is $${8 \over {\sqrt {53} }}$$, then the equation of the other directrix can be :
7
If the coefficients of x7 in $${\left( {{x^2} + {1 \over {bx}}} \right)^{11}}$$ and x$$-$$7 in $${\left( {{x} - {1 \over {bx^2}}} \right)^{11}}$$, b $$\ne$$ 0, are equal, then the value of b is equal to :
8
If $$\sin \theta + \cos \theta = {1 \over 2}$$, then 16(sin(2$$\theta$$) + cos(4$$\theta$$) + sin(6$$\theta$$)) is equal to :
9
Let $$A = \left[ {\matrix{
1 & 2 \cr
{ - 1} & 4 \cr
} } \right]$$. If A$$-$$1 = $$\alpha$$I + $$\beta$$A, $$\alpha$$, $$\beta$$ $$\in$$ R, I is a 2 $$\times$$ 2 identity matrix then 4($$\alpha$$ $$-$$ $$\beta$$) is equal to :
10
Let $$f:\left( { - {\pi \over 4},{\pi \over 4}} \right) \to R$$ be defined as $$f(x) = \left\{ {\matrix{
{{{(1 + |\sin x|)}^{{{3a} \over {|\sin x|}}}}} & , & { - {\pi \over 4} < x < 0} \cr
b & , & {x = 0} \cr
{{e^{\cot 4x/\cot 2x}}} & , & {0 < x < {\pi \over 4}} \cr
} } \right.$$
If f is continuous at x = 0, then the value of 6a + b2 is equal to :
If f is continuous at x = 0, then the value of 6a + b2 is equal to :
11
Let y = y(x) be solution of the differential equation
$${\log _{}}\left( {{{dy} \over {dx}}} \right) = 3x + 4y$$, with y(0) = 0.
If $$y\left( { - {2 \over 3}{{\log }_e}2} \right) = \alpha {\log _e}2$$, then the value of $$\alpha$$ is equal to :
$${\log _{}}\left( {{{dy} \over {dx}}} \right) = 3x + 4y$$, with y(0) = 0.
If $$y\left( { - {2 \over 3}{{\log }_e}2} \right) = \alpha {\log _e}2$$, then the value of $$\alpha$$ is equal to :
12
Let f : R $$\to$$ R be a function such that f(2) = 4 and f'(2) = 1. Then, the value of $$\mathop {\lim }\limits_{x \to 2} {{{x^2}f(2) - 4f(x)} \over {x - 2}}$$ is equal to :
13
Let P and Q be two distinct points on a circle which has center at C(2, 3) and which passes through origin O. If OC is perpendicular to both the line segments CP and CQ, then the set {P, Q} is equal to :
14
Let $$\alpha$$, $$\beta$$ be two roots of the
equation x2 + (20)1/4x + (5)1/2 = 0. Then $$\alpha$$8 + $$\beta$$8 is equal to
equation x2 + (20)1/4x + (5)1/2 = 0. Then $$\alpha$$8 + $$\beta$$8 is equal to
15
The probability that a randomly selected 2-digit number belongs to the set {n $$\in$$ N : (2n $$-$$ 2) is a multiple of 3} is equal to :
16
Let $$A = \{ (x,y) \in R \times R|2{x^2} + 2{y^2} - 2x - 2y = 1\} $$, $$B = \{ (x,y) \in R \times R|4{x^2} + 4{y^2} - 16y + 7 = 0\} $$ and $$C = \{ (x,y) \in R \times R|{x^2} + {y^2} - 4x - 2y + 5 \le {r^2}\} $$.
Then the minimum value of |r| such that $$A \cup B \subseteq C$$ is equal to
Then the minimum value of |r| such that $$A \cup B \subseteq C$$ is equal to
17
For real numbers $$\alpha$$ and $$\beta$$, consider the following system of linear equations :
x + y $$-$$ z = 2, x + 2y + $$\alpha$$z = 1, 2x $$-$$ y + z = $$\beta$$. If the system has infinite solutions, then $$\alpha$$ + $$\beta$$ is equal to ______________.
x + y $$-$$ z = 2, x + 2y + $$\alpha$$z = 1, 2x $$-$$ y + z = $$\beta$$. If the system has infinite solutions, then $$\alpha$$ + $$\beta$$ is equal to ______________.
18
Let $$\overrightarrow a = \widehat i + \widehat j + \widehat k,\overrightarrow b $$ and $$\overrightarrow c = \widehat j - \widehat k$$ be three vectors such that $$\overrightarrow a \times \overrightarrow b = \overrightarrow c $$ and $$\overrightarrow a \,.\,\overrightarrow b = 1$$. If the length of projection vector of the vector $$\overrightarrow b $$ on the vector $$\overrightarrow a \times \overrightarrow c $$ is l, then the value of 3l2 is equal to _____________.
19
If $${\log _3}2,{\log _3}({2^x} - 5),{\log _3}\left( {{2^x} - {7 \over 2}} \right)$$ are in an arithmetic progression, then the value of x is equal to _____________.
20
Let the domain of the function
$$f(x) = {\log _4}\left( {{{\log }_5}\left( {{{\log }_3}(18x - {x^2} - 77)} \right)} \right)$$ be (a, b). Then the value of the integral $$\int\limits_a^b {{{{{\sin }^3}x} \over {({{\sin }^3}x + {{\sin }^3}(a + b - x)}}} dx$$ is equal to _____________.
$$f(x) = {\log _4}\left( {{{\log }_5}\left( {{{\log }_3}(18x - {x^2} - 77)} \right)} \right)$$ be (a, b). Then the value of the integral $$\int\limits_a^b {{{{{\sin }^3}x} \over {({{\sin }^3}x + {{\sin }^3}(a + b - x)}}} dx$$ is equal to _____________.
21
Let $$f(x) = \left| {\matrix{
{{{\sin }^2}x} & { - 2 + {{\cos }^2}x} & {\cos 2x} \cr
{2 + {{\sin }^2}x} & {{{\cos }^2}x} & {\cos 2x} \cr
{{{\sin }^2}x} & {{{\cos }^2}x} & {1 + \cos 2x} \cr
} } \right|,x \in [0,\pi ]$$. Then the maximum value of f(x) is equal to ______________.
22
Let $$F:[3,5] \to R$$ be a twice differentiable function on (3, 5) such that
$$F(x) = {e^{ - x}}\int\limits_3^x {(3{t^2} + 2t + 4F'(t))dt} $$. If $$F'(4) = {{\alpha {e^\beta } - 224} \over {{{({e^\beta } - 4)}^2}}}$$, then $$\alpha$$ + $$\beta$$ is equal to _______________.
$$F(x) = {e^{ - x}}\int\limits_3^x {(3{t^2} + 2t + 4F'(t))dt} $$. If $$F'(4) = {{\alpha {e^\beta } - 224} \over {{{({e^\beta } - 4)}^2}}}$$, then $$\alpha$$ + $$\beta$$ is equal to _______________.
23
Let S = {1, 2, 3, 4, 5, 6, 7}. Then the number of possible functions f : S $$\to$$ S
such that f(m . n) = f(m) . f(n) for every m, n $$\in$$ S and m . n $$\in$$ S is equal to _____________.
such that f(m . n) = f(m) . f(n) for every m, n $$\in$$ S and m . n $$\in$$ S is equal to _____________.
24
If $$y = y(x),y \in \left[ {0,{\pi \over 2}} \right)$$ is the solution of the differential equation $$\sec y{{dy} \over {dx}} - \sin (x + y) - \sin (x - y) = 0$$, with y(0) = 0, then $$5y'\left( {{\pi \over 2}} \right)$$ is equal to ______________.
25
Let $$f:[0,3] \to R$$ be defined by $$f(x) = \min \{ x - [x],1 + [x] - x\} $$ where [x] is the greatest integer less than or equal to x. Let P denote the set containing all x $$\in$$ [0, 3] where f i discontinuous, and Q denote the set containing all x $$\in$$ (0, 3) where f is not differentiable. Then the sum of number of elements in P and Q is equal to ______________.
Physics
1
In the given figure, a battery of emf E is connected across a conductor PQ of length 'l' and different area of cross-sections having radii r1 and r2 (r2 < r1).
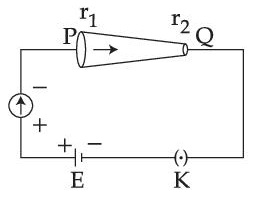
Choose the correct option as one moves from P to Q :

Choose the correct option as one moves from P to Q :
2
The number of molecules in one litre of an ideal gas at 300 K and 2 atmospheric pressure with mean kinetic energy 2 $$\times$$ 10$$-$$9 J per molecules is :
3
The relative permittivity of distilled water is 81. The velocity of light in it will be :
(Given $$\mu$$r = 1)
(Given $$\mu$$r = 1)
4
| List-I | List-II |
|---|---|
| (a) MI of the rod (length L, Mass M, about an axis $$ \bot $$ to the rod passing through the midpoint) | (i) $$8M{L^2}/3$$ |
| (b) MI of the rod (length L, Mass 2M, about an axis $$ \bot $$ to the rod passing through one of its end) | (ii) $$M{L^2}/3$$ |
| (c) MI of the rod (length 2L, Mass M, about an axis $$ \bot $$ to the rod passing through its midpoint) | (iii) $$M{L^2}/12$$ |
| (d) MI of the rod (Length 2L, Mass 2M, about an axis $$ \bot $$ to the rod passing through one of its end) | (iv) $$2M{L^2}/3$$ |
Choose the correct answer from the options given below:
5
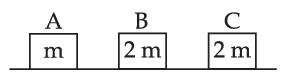
Three objects A, B and C are kept in a straight line on a frictionless horizontal surface. The masses of A, B and C are m, 2m and 2m respectively. A moves towards B with a speed of 9 m/s and makes an elastic collision with it. Thereafter B makes a completely inelastic collision with C. All motions occur along same straight line. The final speed of C is :

6
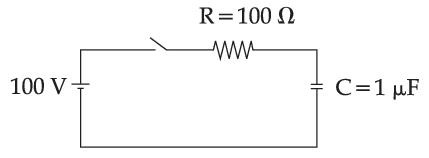
A capacitor of capacitance C = 1 $$\mu$$F is suddenly connected to a battery of 100 volt through a resistance R = 100 $$\Omega$$. The time taken for the capacitor to be charged to get 50 V is :
[Take ln 2 = 0.69]
7
In the reported figure, a capacitor is formed by placing a compound dielectric between the plates of parallel plate capacitor. The expression for the capacity of the said capacitor will be :
(Given area of plate = A)
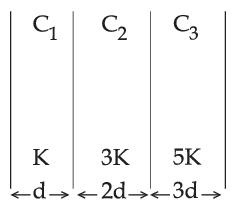
(Given area of plate = A)

8
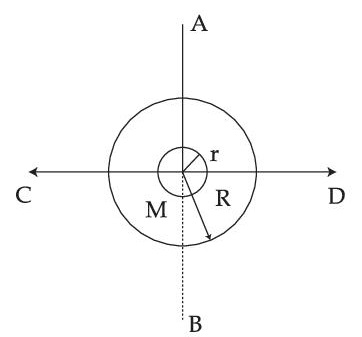
The figure shows two solid discs with radius R and r respectively. If mass per unit area is same for both, what is the ratio of MI of bigger disc around axis AB (Which is $$ \bot $$ to the plane of the disc and passing through its centre) of MI of smaller disc around one of its diameters lying on its plane? Given 'M' is the mass of the larger disc. (MI stands for moment of inertia)

9
In Young's double slit experiment, if the source of light changes from orange to blue then :
10
In the reported figure, there is a cyclic process ABCDA on a sample of 1 mol of a diatomic gas. The temperature of the gas during the process A $$\to$$ B and C $$\to$$ D are T1 and T2 (T1 > T2) respectively.

Choose the correct option out of the following for work done if processes BC and DA are adiabatic.

Choose the correct option out of the following for work done if processes BC and DA are adiabatic.
11
Assertion A : If A, B, C, D are four points on a semi-circular are with centre at 'O' such that $$\left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {BC} } \right| = \left| {\overrightarrow {CD} } \right|$$, then $$\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} = 4\overrightarrow {AO} + \overrightarrow {OB} + \overrightarrow {OC} $$
Reason R : Polygon law of vector addition yields $$\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CD} + \overrightarrow {AD} = 2\overrightarrow {AO} $$
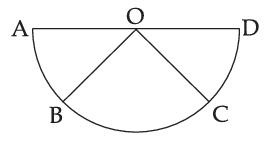
In the light of the above statements, choose the most appropriate answer from the options given below :
Reason R : Polygon law of vector addition yields $$\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CD} + \overrightarrow {AD} = 2\overrightarrow {AO} $$

In the light of the above statements, choose the most appropriate answer from the options given below :
12
A light cylindrical vessel is kept on a horizontal surface. Area of base is A. A hole of cross-sectional area 'a' is made just at its bottom side. The minimum coefficient of friction necessary to prevent sliding the vessel due to the impact force of the emerging liquid is (a < < A) :
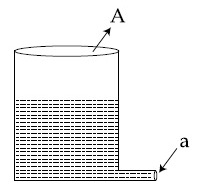

13
A particle starts executing simple harmonic motion (SHM) of amplitude 'a' and total energy E. At any instant, its kinetic energy is $${{3E} \over 4}$$ then its displacement 'y' is given by :
14
Two capacitors of capacities 2C and C are joined in parallel and charged up to potential V. The battery is removed and the capacitor of capacity C is filled completely with a medium of dielectric constant K. The potential difference across the capacitors will now be :
15
A ball is thrown up with a certain velocity so that it reaches a height 'h'. Find the ratio of the two different times of the ball reaching $${h \over 3}$$ in both the directions.
16
A 0.07 H inductor and a 12$$\Omega$$ resistor are connected in series to a 220V, 50 Hz ac source. The approximate current in the circuit and the phase angle between current and source voltage are respectively. [Take $$\pi$$ as $${{22} \over 7}$$]
17
Two identical tennis balls each having mass 'm' and charge 'q' are suspended from a fixed point by threads of length 'l'. What is the equilibrium separation when each thread makes a small angle '$$\theta$$' with the vertical?
18
Assertion A : If in five complete rotations of the circular scale, the distance travelled on main scale of the screw gauge is 5 mm and there are 50 total divisions on circular scale, then least count is 0.001 cm.
Reason R :
Least Count = $${{Pitch} \over {Total\,divisions\,on\,circular\,scale}}$$
In the light of the above statements, choose the most appropriate answer from the options given below :
Reason R :
Least Count = $${{Pitch} \over {Total\,divisions\,on\,circular\,scale}}$$
In the light of the above statements, choose the most appropriate answer from the options given below :
19
Consider an electrical circuit containing a two way switch 'S'. Initially S is open and then T1 is connected to T2. As the current in R = 6$$\Omega$$ attains a maximum value of steady state level, T1 is disconnected from T2 and immediately connected to T3. Potential drop across r = 3$$\Omega$$ resistor immediately after T1 is connected to T3 is __________ V. (Round off to the Nearest Integer)
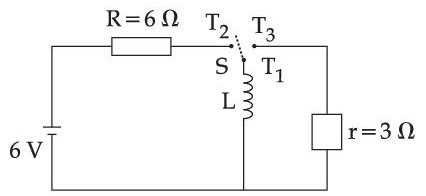

20
Suppose two planets (spherical in shape) in radii R and 2R, but mass M and 9M respectively have a centre to centre separation 8 R as shown in the figure. A satellite of mass 'm' is projected from the surface of the planet of mass 'M' directly towards the centre of the second planet. The minimum speed 'v' required for the satellite to reach the surface of the second planet is $$\sqrt {{a \over 7}{{GM} \over R}} $$ then the value of 'a' is ____________.
[Given : The two planets are fixed in their position]
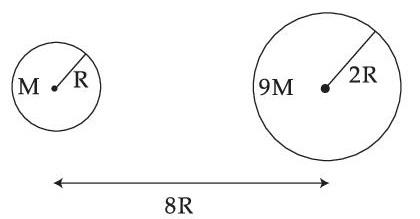
[Given : The two planets are fixed in their position]

21
In Bohr's atomic model, the electron is assumed to revolve in a circular orbit of radius 0.5 $$\mathop A\limits^o $$. If the speed of electron is 2.2 $$\times$$ 166 m/s, then the current associated with the electron will be _____________ $$\times$$ 10$$-$$2 mA. [Take $$\pi$$ as $${{22} \over 7}$$]
22
A particle of mass 9.1 $$\times$$ 10$$-$$31 kg travels in a medium with a speed of 106 m/s and a photon of a radiation of linear momentum 10$$-$$27 kg m/s travels in vacuum. The wavelength of photon is __________ times the wavelength of the particle.
23
A prism of refractive index n1 and another prism of refractive index n2 are stuck together (as shown in the figure). n1 and n2 depend on $$\lambda$$, the wavelength of light, according to the relation
$${n_1} = 1.2 + {{10.8 \times {{10}^{ - 14}}} \over {{\lambda ^2}}}$$ and $${n_2} = 1.45 + {{1.8 \times {{10}^{ - 14}}} \over {{\lambda ^2}}}$$
The wavelength for which rays incident at any angle on the interface BC pass through without bending at that interface will be _____________ nm.

$${n_1} = 1.2 + {{10.8 \times {{10}^{ - 14}}} \over {{\lambda ^2}}}$$ and $${n_2} = 1.45 + {{1.8 \times {{10}^{ - 14}}} \over {{\lambda ^2}}}$$
The wavelength for which rays incident at any angle on the interface BC pass through without bending at that interface will be _____________ nm.

24
A stone of mass 20 g is projected from a rubber catapult of length 0.1 m and area of cross section 10$$-$$6 m2 stretched by an amount 0.04 m. The velocity of the projected stone is ______________ m/s.
(Young's modulus of rubber = 0.5 $$\times$$ 109 N/m2)
(Young's modulus of rubber = 0.5 $$\times$$ 109 N/m2)
25
In a uniform magnetic field, the magnetic needle has a magnetic moment 9.85 $$\times$$ 10$$-$$2 A/m2 and moment of inertia 5 $$\times$$ 10$$-$$6 kg m2. If it performs 10 complete oscillations in 5 seconds then the magnitude of the magnetic field is _______________ mT. [Take $$\pi$$2 as 9.85]
1
JEE Main 2021 (Online) 27th July Morning Shift
MCQ (Single Correct Answer)
+4
-1
The number of molecules in one litre of an ideal gas at 300 K and 2 atmospheric pressure with mean kinetic energy 2 $$\times$$ 10$$-$$9 J per molecules is :
2
JEE Main 2021 (Online) 27th July Morning Shift
MCQ (Single Correct Answer)
+4
-1
The relative permittivity of distilled water is 81. The velocity of light in it will be :
(Given $$\mu$$r = 1)
(Given $$\mu$$r = 1)
3
JEE Main 2021 (Online) 27th July Morning Shift
MCQ (Single Correct Answer)
+4
-1
| List-I | List-II |
|---|---|
| (a) MI of the rod (length L, Mass M, about an axis $$ \bot $$ to the rod passing through the midpoint) | (i) $$8M{L^2}/3$$ |
| (b) MI of the rod (length L, Mass 2M, about an axis $$ \bot $$ to the rod passing through one of its end) | (ii) $$M{L^2}/3$$ |
| (c) MI of the rod (length 2L, Mass M, about an axis $$ \bot $$ to the rod passing through its midpoint) | (iii) $$M{L^2}/12$$ |
| (d) MI of the rod (Length 2L, Mass 2M, about an axis $$ \bot $$ to the rod passing through one of its end) | (iv) $$2M{L^2}/3$$ |
Choose the correct answer from the options given below:
4
JEE Main 2021 (Online) 27th July Morning Shift
MCQ (Single Correct Answer)
+4
-1
Three objects A, B and C are kept in a straight line on a frictionless horizontal surface. The masses of A, B and C are m, 2m and 2m respectively. A moves towards B with a speed of 9 m/s and makes an elastic collision with it. Thereafter B makes a completely inelastic collision with C. All motions occur along same straight line. The final speed of C is :


Subject
Chemistry
22
Mathematics
25
Physics
25
More Papers of JEE Main
2025
JEE Main 2025 (Online) 8th April Evening ShiftJEE Main 2025 (Online) 7th April Evening ShiftJEE Main 2025 (Online) 7th April Morning ShiftJEE Main 2025 (Online) 4th April Evening ShiftJEE Main 2025 (Online) 4th April Morning ShiftJEE Main 2025 (Online) 3rd April Evening ShiftJEE Main 2025 (Online) 3rd April Morning ShiftJEE Main 2025 (Online) 2nd April Evening ShiftJEE Main 2025 (Online) 2nd April Morning ShiftJEE Main 2025 (Online) 29th January Evening ShiftJEE Main 2025 (Online) 29th January Morning ShiftJEE Main 2025 (Online) 28th January Evening ShiftJEE Main 2025 (Online) 28th January Morning ShiftJEE Main 2025 (Online) 24th January Evening ShiftJEE Main 2025 (Online) 24th January Morning ShiftJEE Main 2025 (Online) 23rd January Evening ShiftJEE Main 2025 (Online) 23rd January Morning ShiftJEE Main 2025 (Online) 22nd January Evening ShiftJEE Main 2025 (Online) 22nd January Morning Shift2024
JEE Main 2024 (Online) 9th April Evening ShiftJEE Main 2024 (Online) 9th April Morning ShiftJEE Main 2024 (Online) 8th April Evening ShiftJEE Main 2024 (Online) 8th April Morning ShiftJEE Main 2024 (Online) 6th April Evening ShiftJEE Main 2024 (Online) 6th April Morning ShiftJEE Main 2024 (Online) 5th April Evening ShiftJEE Main 2024 (Online) 5th April Morning ShiftJEE Main 2024 (Online) 4th April Evening ShiftJEE Main 2024 (Online) 4th April Morning ShiftJEE Main 2024 (Online) 1st February Evening ShiftJEE Main 2024 (Online) 1st February Morning ShiftJEE Main 2024 (Online) 31st January Evening ShiftJEE Main 2024 (Online) 31st January Morning ShiftJEE Main 2024 (Online) 30th January Evening ShiftJEE Main 2024 (Online) 30th January Morning ShiftJEE Main 2024 (Online) 29th January Evening ShiftJEE Main 2024 (Online) 29th January Morning ShiftJEE Main 2024 (Online) 27th January Evening ShiftJEE Main 2024 (Online) 27th January Morning Shift2023
JEE Main 2023 (Online) 15th April Morning ShiftJEE Main 2023 (Online) 13th April Evening ShiftJEE Main 2023 (Online) 13th April Morning ShiftJEE Main 2023 (Online) 12th April Morning ShiftJEE Main 2023 (Online) 11th April Evening ShiftJEE Main 2023 (Online) 11th April Morning ShiftJEE Main 2023 (Online) 10th April Evening ShiftJEE Main 2023 (Online) 10th April Morning ShiftJEE Main 2023 (Online) 8th April Evening ShiftJEE Main 2023 (Online) 8th April Morning ShiftJEE Main 2023 (Online) 6th April Evening ShiftJEE Main 2023 (Online) 6th April Morning ShiftJEE Main 2023 (Online) 1st February Evening ShiftJEE Main 2023 (Online) 1st February Morning ShiftJEE Main 2023 (Online) 31st January Evening ShiftJEE Main 2023 (Online) 31st January Morning ShiftJEE Main 2023 (Online) 30th January Evening ShiftJEE Main 2023 (Online) 30th January Morning ShiftJEE Main 2023 (Online) 29th January Evening ShiftJEE Main 2023 (Online) 29th January Morning ShiftJEE Main 2023 (Online) 25th January Evening ShiftJEE Main 2023 (Online) 25th January Morning ShiftJEE Main 2023 (Online) 24th January Evening ShiftJEE Main 2023 (Online) 24th January Morning Shift2022
JEE Main 2022 (Online) 29th July Evening ShiftJEE Main 2022 (Online) 29th July Morning ShiftJEE Main 2022 (Online) 28th July Evening ShiftJEE Main 2022 (Online) 28th July Morning ShiftJEE Main 2022 (Online) 27th July Evening ShiftJEE Main 2022 (Online) 27th July Morning ShiftJEE Main 2022 (Online) 26th July Evening ShiftJEE Main 2022 (Online) 26th July Morning ShiftJEE Main 2022 (Online) 25th July Evening ShiftJEE Main 2022 (Online) 25th July Morning ShiftJEE Main 2022 (Online) 30th June Morning ShiftJEE Main 2022 (Online) 29th June Evening ShiftJEE Main 2022 (Online) 29th June Morning ShiftJEE Main 2022 (Online) 28th June Evening ShiftJEE Main 2022 (Online) 28th June Morning ShiftJEE Main 2022 (Online) 27th June Evening ShiftJEE Main 2022 (Online) 27th June Morning ShiftJEE Main 2022 (Online) 26th June Evening ShiftJEE Main 2022 (Online) 26th June Morning ShiftJEE Main 2022 (Online) 25th June Evening ShiftJEE Main 2022 (Online) 25th June Morning ShiftJEE Main 2022 (Online) 24th June Evening ShiftJEE Main 2022 (Online) 24th June Morning Shift2021
JEE Main 2021 (Online) 1st September Evening ShiftJEE Main 2021 (Online) 31st August Evening ShiftJEE Main 2021 (Online) 31st August Morning ShiftJEE Main 2021 (Online) 27th August Evening ShiftJEE Main 2021 (Online) 27th August Morning ShiftJEE Main 2021 (Online) 26th August Evening ShiftJEE Main 2021 (Online) 26th August Morning ShiftJEE Main 2021 (Online) 27th July Evening ShiftJEE Main 2021 (Online) 27th July Morning ShiftJEE Main 2021 (Online) 25th July Evening ShiftJEE Main 2021 (Online) 25th July Morning ShiftJEE Main 2021 (Online) 22th July Evening ShiftJEE Main 2021 (Online) 20th July Evening ShiftJEE Main 2021 (Online) 20th July Morning ShiftJEE Main 2021 (Online) 18th March Evening ShiftJEE Main 2021 (Online) 18th March Morning ShiftJEE Main 2021 (Online) 17th March Evening ShiftJEE Main 2021 (Online) 17th March Morning ShiftJEE Main 2021 (Online) 16th March Evening ShiftJEE Main 2021 (Online) 16th March Morning ShiftJEE Main 2021 (Online) 26th February Evening ShiftJEE Main 2021 (Online) 26th February Morning ShiftJEE Main 2021 (Online) 25th February Evening ShiftJEE Main 2021 (Online) 25th February Morning ShiftJEE Main 2021 (Online) 24th February Evening ShiftJEE Main 2021 (Online) 24th February Morning Shift2020
JEE Main 2020 (Online) 6th September Evening SlotJEE Main 2020 (Online) 6th September Morning SlotJEE Main 2020 (Online) 5th September Evening SlotJEE Main 2020 (Online) 5th September Morning SlotJEE Main 2020 (Online) 4th September Evening SlotJEE Main 2020 (Online) 4th September Morning SlotJEE Main 2020 (Online) 3rd September Evening SlotJEE Main 2020 (Online) 3rd September Morning SlotJEE Main 2020 (Online) 2nd September Evening SlotJEE Main 2020 (Online) 2nd September Morning SlotJEE Main 2020 (Online) 9th January Evening SlotJEE Main 2020 (Online) 9th January Morning SlotJEE Main 2020 (Online) 8th January Evening SlotJEE Main 2020 (Online) 8th January Morning SlotJEE Main 2020 (Online) 7th January Evening SlotJEE Main 2020 (Online) 7th January Morning Slot2019
JEE Main 2019 (Online) 12th April Evening SlotJEE Main 2019 (Online) 12th April Morning SlotJEE Main 2019 (Online) 10th April Evening SlotJEE Main 2019 (Online) 10th April Morning SlotJEE Main 2019 (Online) 9th April Evening SlotJEE Main 2019 (Online) 9th April Morning SlotJEE Main 2019 (Online) 8th April Evening SlotJEE Main 2019 (Online) 8th April Morning SlotJEE Main 2019 (Online) 12th January Evening SlotJEE Main 2019 (Online) 12th January Morning SlotJEE Main 2019 (Online) 11th January Evening SlotJEE Main 2019 (Online) 11th January Morning SlotJEE Main 2019 (Online) 10th January Evening SlotJEE Main 2019 (Online) 10th January Morning SlotJEE Main 2019 (Online) 9th January Evening SlotJEE Main 2019 (Online) 9th January Morning Slot2018
JEE Main 2018 (Online) 16th April Morning SlotJEE Main 2018 (Offline)JEE Main 2018 (Online) 15th April Evening SlotJEE Main 2018 (Online) 15th April Morning Slot2017
JEE Main 2017 (Online) 9th April Morning SlotJEE Main 2017 (Online) 8th April Morning SlotJEE Main 2017 (Offline)2016
JEE Main 2016 (Online) 10th April Morning SlotJEE Main 2016 (Online) 9th April Morning SlotJEE Main 2016 (Offline)2015
JEE Main 2015 (Offline)2014
JEE Main 2014 (Offline)2013
JEE Main 2013 (Offline)2012
AIEEE 20122011
AIEEE 20112010
AIEEE 20102009
AIEEE 20092008
AIEEE 20082007
AIEEE 20072006
AIEEE 20062005
AIEEE 20052004
AIEEE 20042003
AIEEE 20032002
AIEEE 2002