2025
JEE Main 2025 (Online) 8th April Evening ShiftJEE Main 2025 (Online) 7th April Evening ShiftJEE Main 2025 (Online) 7th April Morning ShiftJEE Main 2025 (Online) 4th April Evening ShiftJEE Main 2025 (Online) 4th April Morning ShiftJEE Main 2025 (Online) 3rd April Evening ShiftJEE Main 2025 (Online) 3rd April Morning ShiftJEE Main 2025 (Online) 2nd April Evening ShiftJEE Main 2025 (Online) 2nd April Morning ShiftJEE Main 2025 (Online) 29th January Evening ShiftJEE Main 2025 (Online) 29th January Morning ShiftJEE Main 2025 (Online) 28th January Evening ShiftJEE Main 2025 (Online) 28th January Morning ShiftJEE Main 2025 (Online) 24th January Evening ShiftJEE Main 2025 (Online) 24th January Morning ShiftJEE Main 2025 (Online) 23rd January Evening ShiftJEE Main 2025 (Online) 23rd January Morning ShiftJEE Main 2025 (Online) 22nd January Evening ShiftJEE Main 2025 (Online) 22nd January Morning Shift2024
JEE Main 2024 (Online) 9th April Evening ShiftJEE Main 2024 (Online) 9th April Morning ShiftJEE Main 2024 (Online) 8th April Evening ShiftJEE Main 2024 (Online) 8th April Morning ShiftJEE Main 2024 (Online) 6th April Evening ShiftJEE Main 2024 (Online) 6th April Morning ShiftJEE Main 2024 (Online) 5th April Evening ShiftJEE Main 2024 (Online) 5th April Morning ShiftJEE Main 2024 (Online) 4th April Evening ShiftJEE Main 2024 (Online) 4th April Morning ShiftJEE Main 2024 (Online) 1st February Evening ShiftJEE Main 2024 (Online) 1st February Morning ShiftJEE Main 2024 (Online) 31st January Evening ShiftJEE Main 2024 (Online) 31st January Morning ShiftJEE Main 2024 (Online) 30th January Evening ShiftJEE Main 2024 (Online) 30th January Morning ShiftJEE Main 2024 (Online) 29th January Evening ShiftJEE Main 2024 (Online) 29th January Morning ShiftJEE Main 2024 (Online) 27th January Evening ShiftJEE Main 2024 (Online) 27th January Morning Shift2023
JEE Main 2023 (Online) 15th April Morning ShiftJEE Main 2023 (Online) 13th April Evening ShiftJEE Main 2023 (Online) 13th April Morning ShiftJEE Main 2023 (Online) 12th April Morning ShiftJEE Main 2023 (Online) 11th April Evening ShiftJEE Main 2023 (Online) 11th April Morning ShiftJEE Main 2023 (Online) 10th April Evening ShiftJEE Main 2023 (Online) 10th April Morning ShiftJEE Main 2023 (Online) 8th April Evening ShiftJEE Main 2023 (Online) 8th April Morning ShiftJEE Main 2023 (Online) 6th April Evening ShiftJEE Main 2023 (Online) 6th April Morning ShiftJEE Main 2023 (Online) 1st February Evening ShiftJEE Main 2023 (Online) 1st February Morning ShiftJEE Main 2023 (Online) 31st January Evening ShiftJEE Main 2023 (Online) 31st January Morning ShiftJEE Main 2023 (Online) 30th January Evening ShiftJEE Main 2023 (Online) 30th January Morning ShiftJEE Main 2023 (Online) 29th January Evening ShiftJEE Main 2023 (Online) 29th January Morning ShiftJEE Main 2023 (Online) 25th January Evening ShiftJEE Main 2023 (Online) 25th January Morning ShiftJEE Main 2023 (Online) 24th January Evening ShiftJEE Main 2023 (Online) 24th January Morning Shift2022
JEE Main 2022 (Online) 29th July Evening ShiftJEE Main 2022 (Online) 29th July Morning ShiftJEE Main 2022 (Online) 28th July Evening ShiftJEE Main 2022 (Online) 28th July Morning ShiftJEE Main 2022 (Online) 27th July Evening ShiftJEE Main 2022 (Online) 27th July Morning ShiftJEE Main 2022 (Online) 26th July Evening ShiftJEE Main 2022 (Online) 26th July Morning ShiftJEE Main 2022 (Online) 25th July Evening ShiftJEE Main 2022 (Online) 25th July Morning ShiftJEE Main 2022 (Online) 30th June Morning ShiftJEE Main 2022 (Online) 29th June Evening ShiftJEE Main 2022 (Online) 29th June Morning ShiftJEE Main 2022 (Online) 28th June Evening ShiftJEE Main 2022 (Online) 28th June Morning ShiftJEE Main 2022 (Online) 27th June Evening ShiftJEE Main 2022 (Online) 27th June Morning ShiftJEE Main 2022 (Online) 26th June Evening ShiftJEE Main 2022 (Online) 26th June Morning ShiftJEE Main 2022 (Online) 25th June Evening ShiftJEE Main 2022 (Online) 25th June Morning ShiftJEE Main 2022 (Online) 24th June Evening ShiftJEE Main 2022 (Online) 24th June Morning Shift2021
JEE Main 2021 (Online) 1st September Evening ShiftJEE Main 2021 (Online) 31st August Evening ShiftJEE Main 2021 (Online) 31st August Morning ShiftJEE Main 2021 (Online) 27th August Evening ShiftJEE Main 2021 (Online) 27th August Morning ShiftJEE Main 2021 (Online) 26th August Evening ShiftJEE Main 2021 (Online) 26th August Morning ShiftJEE Main 2021 (Online) 27th July Evening ShiftJEE Main 2021 (Online) 27th July Morning ShiftJEE Main 2021 (Online) 25th July Evening ShiftJEE Main 2021 (Online) 25th July Morning ShiftJEE Main 2021 (Online) 22th July Evening ShiftJEE Main 2021 (Online) 20th July Evening ShiftJEE Main 2021 (Online) 20th July Morning ShiftJEE Main 2021 (Online) 18th March Evening ShiftJEE Main 2021 (Online) 18th March Morning ShiftJEE Main 2021 (Online) 17th March Evening ShiftJEE Main 2021 (Online) 17th March Morning ShiftJEE Main 2021 (Online) 16th March Evening ShiftJEE Main 2021 (Online) 16th March Morning ShiftJEE Main 2021 (Online) 26th February Evening ShiftJEE Main 2021 (Online) 26th February Morning ShiftJEE Main 2021 (Online) 25th February Evening ShiftJEE Main 2021 (Online) 25th February Morning ShiftJEE Main 2021 (Online) 24th February Evening ShiftJEE Main 2021 (Online) 24th February Morning Shift2020
JEE Main 2020 (Online) 6th September Evening SlotJEE Main 2020 (Online) 6th September Morning SlotJEE Main 2020 (Online) 5th September Evening SlotJEE Main 2020 (Online) 5th September Morning SlotJEE Main 2020 (Online) 4th September Evening SlotJEE Main 2020 (Online) 4th September Morning SlotJEE Main 2020 (Online) 3rd September Evening SlotJEE Main 2020 (Online) 3rd September Morning SlotJEE Main 2020 (Online) 2nd September Evening SlotJEE Main 2020 (Online) 2nd September Morning SlotJEE Main 2020 (Online) 9th January Evening SlotJEE Main 2020 (Online) 9th January Morning SlotJEE Main 2020 (Online) 8th January Evening SlotJEE Main 2020 (Online) 8th January Morning SlotJEE Main 2020 (Online) 7th January Evening SlotJEE Main 2020 (Online) 7th January Morning Slot2019
JEE Main 2019 (Online) 12th April Evening SlotJEE Main 2019 (Online) 12th April Morning SlotJEE Main 2019 (Online) 10th April Evening SlotJEE Main 2019 (Online) 10th April Morning SlotJEE Main 2019 (Online) 9th April Evening SlotJEE Main 2019 (Online) 9th April Morning SlotJEE Main 2019 (Online) 8th April Evening SlotJEE Main 2019 (Online) 8th April Morning SlotJEE Main 2019 (Online) 12th January Evening SlotJEE Main 2019 (Online) 12th January Morning SlotJEE Main 2019 (Online) 11th January Evening SlotJEE Main 2019 (Online) 11th January Morning SlotJEE Main 2019 (Online) 10th January Evening SlotJEE Main 2019 (Online) 10th January Morning SlotJEE Main 2019 (Online) 9th January Evening SlotJEE Main 2019 (Online) 9th January Morning Slot2018
JEE Main 2018 (Online) 16th April Morning SlotJEE Main 2018 (Offline)JEE Main 2018 (Online) 15th April Evening SlotJEE Main 2018 (Online) 15th April Morning Slot2017
JEE Main 2017 (Online) 9th April Morning SlotJEE Main 2017 (Online) 8th April Morning SlotJEE Main 2017 (Offline)2016
JEE Main 2016 (Online) 10th April Morning SlotJEE Main 2016 (Online) 9th April Morning SlotJEE Main 2016 (Offline)2015
JEE Main 2015 (Offline)2014
JEE Main 2014 (Offline)2013
JEE Main 2013 (Offline)2012
AIEEE 20122011
AIEEE 20112010
AIEEE 20102009
AIEEE 20092008
AIEEE 20082007
AIEEE 20072006
AIEEE 20062005
AIEEE 20052004
AIEEE 20042003
AIEEE 20032002
AIEEE 2002JEE Main 2021 (Online) 27th July Evening Shift
Paper was held on Tue, Jul 27, 2021 9:30 AM
Chemistry
1

Consider the above reaction, the major product "P" formed is :
2
Given below are two statement : one is labelled as Assertion A and the other is labelled as Reason R.
Assertion A : SO2(g) is absorbed to a large extent than H2(g) on activated charcoal.
Reason R : SO2(g) has a higher critical temperature than H2(g).
In the light of the above statements, choose the most appropriate answer from the options given below.
Assertion A : SO2(g) is absorbed to a large extent than H2(g) on activated charcoal.
Reason R : SO2(g) has a higher critical temperature than H2(g).
In the light of the above statements, choose the most appropriate answer from the options given below.
3
The correct order of first ionisation enthalpy is :
4
Given below are two statements :
Statement I : Hyperconjugation is a permanent effect.
Statement II : Hyperconjugation in ethyl cation $$\left( {C{H_3} - \mathop C\limits^ + {H_2}} \right)$$ involves the overlapping of $${C_{s{p^2}}} - {H_{1s}}$$ bond with empty 2p orbital of other carbon.
Choose the correct option :
Statement I : Hyperconjugation is a permanent effect.
Statement II : Hyperconjugation in ethyl cation $$\left( {C{H_3} - \mathop C\limits^ + {H_2}} \right)$$ involves the overlapping of $${C_{s{p^2}}} - {H_{1s}}$$ bond with empty 2p orbital of other carbon.
Choose the correct option :
5
Given below are two statements :
Statement I : $${[Mn{(CN)_6}]^{3 - }}$$, $${[Fe{(CN)_6}]^{3 - }}$$ and $${[Co{({C_2}{O_4})_3}]^{3 - }}$$ are d2sp3 hybridised.
Statement II : $${[MnCl)_6}{]^{3 - }}$$ and $${[Fe{F_6}]^{3 - }}$$ are paramagnetic and have 4 and 5 unpaired electrons, respectively.
In the light of the above statements, choose the correct answer from the options given below :
Statement I : $${[Mn{(CN)_6}]^{3 - }}$$, $${[Fe{(CN)_6}]^{3 - }}$$ and $${[Co{({C_2}{O_4})_3}]^{3 - }}$$ are d2sp3 hybridised.
Statement II : $${[MnCl)_6}{]^{3 - }}$$ and $${[Fe{F_6}]^{3 - }}$$ are paramagnetic and have 4 and 5 unpaired electrons, respectively.
In the light of the above statements, choose the correct answer from the options given below :
6
To an aqueous solution containing ions such as Al3+, Zn2+, Ca2+, Fe3+, Ni2+, Ba2+ and Cu2+ was added conc. HCl, followed by H2S.
The total number of cations precipitated during this reaction is/are :
The total number of cations precipitated during this reaction is/are :
7
Compound A gives D-Galactose and D-Glucose on hydrolysis. The compound A is :
8
$$R - CN\mathrel{\mathop{\kern0pt\longrightarrow}
\limits_{(ii){H_2}O}^{(i)DIBAL - H}} R - Y$$
Consider the above reaction and identify "Y"
Consider the above reaction and identify "Y"
9

Consider the above reaction, and choose the correct statement :
10
Match List - I with List - II :
Choose the correct answer from the options given below :
| List - I (compound) |
List - II (effect/affected species) |
||
|---|---|---|---|
| (a) | Carbon monoxide | (i) | Carcinogenic |
| (b) | Sulphur dioxide | (ii) | Metabolized by pyrus plants |
| (c) | Polychlorinated biphenyls | (iii) | haemoglobin |
| (d) | Oxides of Nitrogen | (iv) | Stiffness of flower buds |
Choose the correct answer from the options given below :
11
What is A in the following reaction?


12
The correct sequence of correct reagents for the following transformation is :


13
The equilibrium constant for the reaction
A(s) $$\rightleftharpoons$$ M(s) + $${1 \over 2}$$O2(g)
is Kp = 4. At equilibrium, the partial pressure of O2 is _________ atm. (Round off to the nearest integer)
A(s) $$\rightleftharpoons$$ M(s) + $${1 \over 2}$$O2(g)
is Kp = 4. At equilibrium, the partial pressure of O2 is _________ atm. (Round off to the nearest integer)
14
When 400 mL of 0.2 M H2SO4 solution is mixed with 600 mL of 0.1 M NaOH solution, the increase in temperature of the final solution is __________ $$\times$$ 10$$-$$2 K. (Round off to the nearest integer).
[Use : H+ (aq) + OH$$-$$ (aq) $$\to$$ H2O : $$\Delta$$$$\gamma$$H = $$-$$57.1 kJ mol$$-$$1]
Specific heat of H2O = 4.18 J K$$-$$1 g$$-$$1
density of H2O = 1.0 g cm$$-$$3
Assume no change in volume of solution on mixing.
[Use : H+ (aq) + OH$$-$$ (aq) $$\to$$ H2O : $$\Delta$$$$\gamma$$H = $$-$$57.1 kJ mol$$-$$1]
Specific heat of H2O = 4.18 J K$$-$$1 g$$-$$1
density of H2O = 1.0 g cm$$-$$3
Assume no change in volume of solution on mixing.
15
2SO2(g) + O2(g) $$\to$$ 2SO3(g)
The above reaction is carried out in a vessel starting with partial pressure PSO2 = 250 m bar, PO2 = 750 m bar and PSO3 = 0 bar. When the reaction is complete, the total pressure in the reaction vessel is _______ m bar. (Round off of the nearest integer).
The above reaction is carried out in a vessel starting with partial pressure PSO2 = 250 m bar, PO2 = 750 m bar and PSO3 = 0 bar. When the reaction is complete, the total pressure in the reaction vessel is _______ m bar. (Round off of the nearest integer).
16
10.0 mL of 0.05 M KMnO4 solution was consumed in a titration with 10.0 mL of given oxalic acid dihydrate solution. The strength of given oxalic acid solution is _________ $$\times$$ 10$$-$$2 g/L.
(Round off to the nearest integer)
(Round off to the nearest integer)
17
The total number of electrons in all bonding molecular orbitals of $$O_2^{2 - }$$ is ______________.
(Round off to the nearest integer)
(Round off to the nearest integer)
18
3 moles of metal complex with formula Co(en)2Cl3 gives 3 moles of silver chloride on treatment with excess of silver nitrate. The secondary valency of Co in the complex is ___________.
(Round off to the nearest integer)
(Round off to the nearest integer)
19
In a solvent 50% of an acid HA dimerizes and the rest dissociates. The van't Hoff factor of the acid is __________ $$\times$$ 10$$-$$2.
(Round off to the nearest integer)
(Round off to the nearest integer)
20
The dihedral angle in staggered form of Newman projection of 1, 1, 1-Trichloro ethane is ___________ degree. (Round off to the nearest integer)
21
For the first order reaction A $$\to$$ 2B, 1 mole of reactant A gives 0.2 moles of B after 100 minutes. The half life of the reaction is __________ min. (Round off to the nearest integer).
[Use : ln 2 = 0.69, ln 10 = 2.3]
Properties of logarithms : ln xy = y ln x;
$$\ln \left( {{x \over y}} \right) = \ln x - \ln y$$
(Round off to the nearest integer)
[Use : ln 2 = 0.69, ln 10 = 2.3]
Properties of logarithms : ln xy = y ln x;
$$\ln \left( {{x \over y}} \right) = \ln x - \ln y$$
(Round off to the nearest integer)
22
For the cell
Cu(s) | Cu2+ (aq) (0.1 M) || Ag+(aq) (0.01 M) | Ag(s)
the cell potential E1 = 0.3095 V
For the cell
Cu(s) | Cu2+ (aq) (0.01 M) || Ag+(aq) (0.001 M) | Ag(s)
the cell potential = ____________ $$\times$$ 10$$-$$2 V. (Round off the nearest integer).
[Use : $${{2.303RT} \over F}$$ = 0.059]
Cu(s) | Cu2+ (aq) (0.1 M) || Ag+(aq) (0.01 M) | Ag(s)
the cell potential E1 = 0.3095 V
For the cell
Cu(s) | Cu2+ (aq) (0.01 M) || Ag+(aq) (0.001 M) | Ag(s)
the cell potential = ____________ $$\times$$ 10$$-$$2 V. (Round off the nearest integer).
[Use : $${{2.303RT} \over F}$$ = 0.059]
Mathematics
1
The point P (a, b) undergoes the following three transformations successively :
(a) reflection about the line y = x.
(b) translation through 2 units along the positive direction of x-axis.
(c) rotation through angle $${\pi \over 4}$$ about the origin in the anti-clockwise direction.
If the co-ordinates of the final position of the point P are $$\left( { - {1 \over {\sqrt 2 }},{7 \over {\sqrt 2 }}} \right)$$, then the value of 2a + b is equal to :
(a) reflection about the line y = x.
(b) translation through 2 units along the positive direction of x-axis.
(c) rotation through angle $${\pi \over 4}$$ about the origin in the anti-clockwise direction.
If the co-ordinates of the final position of the point P are $$\left( { - {1 \over {\sqrt 2 }},{7 \over {\sqrt 2 }}} \right)$$, then the value of 2a + b is equal to :
2
A possible value of 'x', for which the ninth term in the expansion of $${\left\{ {{3^{{{\log }_3}\sqrt {{{25}^{x - 1}} + 7} }} + {3^{\left( { - {1 \over 8}} \right){{\log }_3}({5^{x - 1}} + 1)}}} \right\}^{10}}$$ in the increasing powers of $${3^{\left( { - {1 \over 8}} \right){{\log }_3}({5^{x - 1}} + 1)}}$$ is equal to 180, is :
3
Let f : R $$\to$$ R be defined as $$f(x + y) + f(x - y) = 2f(x)f(y),f\left( {{1 \over 2}} \right) = - 1$$. Then, the value of $$\sum\limits_{k = 1}^{20} {{1 \over {\sin (k)\sin (k + f(k))}}} $$ is equal to :
4
Let C be the set of all complex numbers. Let
S1 = {z$$\in$$C : |z $$-$$ 2| $$\le$$ 1} and
S2 = {z$$\in$$C : z(1 + i) + $$\overline z $$(1 $$-$$ i) $$\ge$$ 4}.
Then, the maximum value of $${\left| {z - {5 \over 2}} \right|^2}$$ for z$$\in$$S1 $$\cap$$ S2 is equal to :
S1 = {z$$\in$$C : |z $$-$$ 2| $$\le$$ 1} and
S2 = {z$$\in$$C : z(1 + i) + $$\overline z $$(1 $$-$$ i) $$\ge$$ 4}.
Then, the maximum value of $${\left| {z - {5 \over 2}} \right|^2}$$ for z$$\in$$S1 $$\cap$$ S2 is equal to :
5
If $$\tan \left( {{\pi \over 9}} \right),x,\tan \left( {{{7\pi } \over {18}}} \right)$$ are in arithmetic progression and $$\tan \left( {{\pi \over 9}} \right),y,\tan \left( {{{5\pi } \over {18}}} \right)$$ are also in arithmetic progression, then $$|x - 2y|$$ is equal to :
6
Let the mean and variance of the frequency distribution
$$\matrix{ {x:} & {{x_1} = 2} & {{x_2} = 6} & {{x_3} = 8} & {{x_4} = 9} \cr {f:} & 4 & 4 & \alpha & \beta \cr } $$
be 6 and 6.8 respectively. If x3 is changed from 8 to 7, then the mean for the new data will be :
$$\matrix{ {x:} & {{x_1} = 2} & {{x_2} = 6} & {{x_3} = 8} & {{x_4} = 9} \cr {f:} & 4 & 4 & \alpha & \beta \cr } $$
be 6 and 6.8 respectively. If x3 is changed from 8 to 7, then the mean for the new data will be :
7
The area of the region bounded by y $$-$$ x = 2 and x2 = y is equal to :
8
Let y = y(x) be the solution of the differential
equation (x $$-$$ x3)dy = (y + yx2 $$-$$ 3x4)dx, x > 2. If y(3) = 3, then y(4) is equal to :
equation (x $$-$$ x3)dy = (y + yx2 $$-$$ 3x4)dx, x > 2. If y(3) = 3, then y(4) is equal to :
9
The value of
$$\mathop {\lim }\limits_{x \to 0} \left( {{x \over {\root 8 \of {1 - \sin x} - \root 8 \of {1 + \sin x} }}} \right)$$ is equal to :
$$\mathop {\lim }\limits_{x \to 0} \left( {{x \over {\root 8 \of {1 - \sin x} - \root 8 \of {1 + \sin x} }}} \right)$$ is equal to :
10
Two sides of a parallelogram are along the lines 4x + 5y = 0 and 7x + 2y = 0. If the equation of one of the diagonals of the parallelogram is 11x + 7y = 9, then other diagonal passes through the point :
11
Let $$\alpha = \mathop {\max }\limits_{x \in R} \{ {8^{2\sin 3x}}{.4^{4\cos 3x}}\} $$ and $$\beta = \mathop {\min }\limits_{x \in R} \{ {8^{2\sin 3x}}{.4^{4\cos 3x}}\} $$. If $$8{x^2} + bx + c = 0$$ is a quadratic equation whose roots are $$\alpha$$1/5 and $$\beta$$1/5, then the value of c $$-$$ b is equal to :
12
Let $$f:[0,\infty ) \to [0,3]$$ be a function defined by
$$f(x) = \left\{ {\matrix{ {\max \{ \sin t:0 \le t \le x\} ,} & {0 \le x \le \pi } \cr {2 + \cos x,} & {x > \pi } \cr } } \right.$$
Then which of the following is true?
$$f(x) = \left\{ {\matrix{ {\max \{ \sin t:0 \le t \le x\} ,} & {0 \le x \le \pi } \cr {2 + \cos x,} & {x > \pi } \cr } } \right.$$
Then which of the following is true?
13
Let N be the set of natural numbers and a relation R on N be defined by $$R = \{ (x,y) \in N \times N:{x^3} - 3{x^2}y - x{y^2} + 3{y^3} = 0\} $$. Then the relation R is :
14
Consider a circle C which touches the y-axis at (0, 6) and cuts off an intercept $$6\sqrt 5 $$ on the x-axis. Then the radius of the circle C is equal to :
15
Let f : (a, b) $$\to$$ R be twice differentiable function such that $$f(x) = \int_a^x {g(t)dt} $$ for a differentiable function g(x). If f(x) = 0 has exactly five distinct roots in (a, b), then g(x)g'(x) = 0 has at least :
16
If the real part of the complex number $$z = {{3 + 2i\cos \theta } \over {1 - 3i\cos \theta }},\theta \in \left( {0,{\pi \over 2}} \right)$$ is zero, then the value of sin23$$\theta$$ + cos2$$\theta$$ is equal to _______________.
17
If $$\int_0^\pi {({{\sin }^3}x){e^{ - {{\sin }^2}x}}dx = \alpha - {\beta \over e}\int_0^1 {\sqrt t {e^t}dt} } $$, then $$\alpha$$ + $$\beta$$ is equal to ____________.
18
The number of real roots of the equation e4x $$-$$ e3x $$-$$ 4e2x $$-$$ ex + 1 = 0 is equal to ______________.
19
Let y = y(x) be the solution of the differential equation dy = e$$\alpha$$x + y dx; $$\alpha$$ $$\in$$ N. If y(loge2) = loge2 and y(0) = loge$$\left( {{1 \over 2}} \right)$$, then the value of $$\alpha$$ is equal to _____________.
20
Let n be a non-negative integer. Then the number of divisors of the form "4n + 1" of the number (10)10 . (11)11 . (13)13 is equal to __________.
21
Let A = {n $$\in$$ N | n2 $$\le$$ n + 10,000}, B = {3k + 1 | k$$\in$$ N} an dC = {2k | k$$\in$$N}, then the sum of all the elements of the set A $$\cap$$(B $$-$$ C) is equal to _____________.
22
If $$A = \left[ {\matrix{
1 & 1 & 1 \cr
0 & 1 & 1 \cr
0 & 0 & 1 \cr
} } \right]$$ and M = A + A2 + A3 + ....... + A20, then the sum of all the elements of the matrix M is equal to _____________.
Physics
1
An electron and proton are separated by a large distance. The electron starts approaching the proton with energy 3 eV. The proton captures the electron and forms a hydrogen atom in second excited state. The resulting photon is incident on a photosensitive metal of threshold wavelength 4000$$\mathop A\limits^o $$. What is the maximum kinetic energy of the emitted photoelectron?
2
The expected graphical representation of the variation of angle of deviation '$$\delta$$' with angle of incidence 'i' in a prism is :
3
A raindrop with radius R = 0.2 mm falls from a cloud at a height h = 2000 m above the ground. Assume that the drop is spherical throughout its fall and the force of buoyance may be neglected, then the terminal speed attained by the raindrop is :
[Density of water fw = 1000 kg m$$-$$3 and Density of air fa = 1.2 kg m$$-$$3, g = 10 m/s2, Coefficient of viscosity of air = 1.8 $$\times$$ 10$$-$$5 Nsm$$-$$2]
[Density of water fw = 1000 kg m$$-$$3 and Density of air fa = 1.2 kg m$$-$$3, g = 10 m/s2, Coefficient of viscosity of air = 1.8 $$\times$$ 10$$-$$5 Nsm$$-$$2]
4
One mole of an ideal gas is taken through an adiabatic process where the temperature rises from 27$$^\circ$$ C to 37$$^\circ$$ C. If the ideal gas is composed of polyatomic molecule that has 4 vibrational modes, which of the following is true? [R = 8.314 J mol$$-$$1 k$$-$$1]
5
An object of mass 0.5 kg is executing simple harmonic motion. It amplitude is 5 cm and time period (T) is 0.2 s. What will be the potential energy of the object at an instant $$t = {T \over 4}s$$ starting from mean position. Assume that the initial phase of the oscillation is zero.
6
Match List I with List II.
Choose the correct answer from the options given below
| List - I | List - II | ||
|---|---|---|---|
| (a) | Capacitance, C | (i) | $${M^1}{L^1}{T^{ - 3}}{A^{ - 1}}$$ |
| (b) | Permittivity of free space, $${\varepsilon _0}$$ | (ii) | $${M^{ - 1}}{L^{ - 3}}{T^4}{A^2}$$ |
| (c) | Permeability of free space, $${\mu _0}$$ | (iii) | $${M^{ - 1}}{L^{ - 2}}{T^4}{A^2}$$ |
| (d) | Electric field, E | (iv) | $${M^1}{L^1}{T^{ - 2}}{A^{ - 2}}$$ |
Choose the correct answer from the options given below
7
Given below is the plot of a potential energy function U(x) for a system, in which a particle is in one dimensional motion, while a conservative force F(x) acts on it. Suppose that Emech = 8 J, the incorrect statement for this system is :
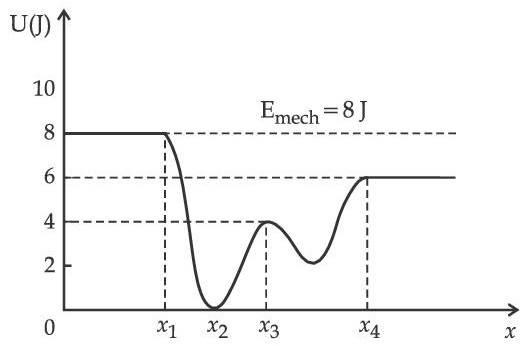
[ where K.E. = kinetic energy ]

[ where K.E. = kinetic energy ]
8
A 100$$\Omega$$ resistance, a 0.1 $$\mu$$F capacitor and an inductor are connected in series across a 250 V supply at variable frequency. Calculate the value of inductance of inductor at which resonance will occur. Given that the resonant frequency is 60 Hz.
9
A simple pendulum of mass 'm', length 'l' and charge '+ q' suspended in the electric field produced by two conducting parallel plates as shown. The value of deflection of pendulum in equilibrium position will be


10
Find the truth table for the function Y of A and B represented in the following figure.


11
Figure A and B shown to long straight wires of circular cross-section (a and b with a < b), carrying current I which is uniformly distributed across the cross-section. The magnitude of magnetic field B varies with radius r and can be represented as :
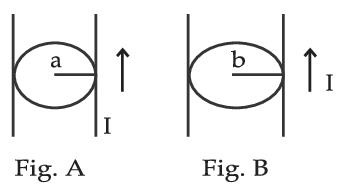

12
Two identical particles of mass 1 kg each go round a circle of radius R, under the action of their mutual gravitational attraction. The angular speed of each particle is :
13
What will be the magnitude of electric field at point O as shown in the figure? Each side of the figure is l and perpendicular to each other?


14
A physical quantity 'y' is represented by the formula $$y = {m^2}{r^{ - 4}}{g^x}{l^{ - {3 \over 2}}}$$
If the percentage errors found in y, m, r, l and g are 18, 1, 0.5, 4 and p respectively, then find the value of x and p.
If the percentage errors found in y, m, r, l and g are 18, 1, 0.5, 4 and p respectively, then find the value of x and p.
15
An automobile of mass 'm' accelerates starting from origin and initially at rest, while the engine supplies constant power P. The position is given as a function of time by :
16
The planet Mars has two moons, if one of them has a period 7 hours, 30 minutes and an orbital radius of 9.0 $$\times$$ 103 km. Find the mass of Mars.
$$\left\{ {Given\,{{4{\pi ^2}} \over G} = 6 \times {{10}^{11}}{N^{ - 1}}{m^{ - 2}}k{g^2}} \right\}$$
$$\left\{ {Given\,{{4{\pi ^2}} \over G} = 6 \times {{10}^{11}}{N^{ - 1}}{m^{ - 2}}k{g^2}} \right\}$$
17
A particle of mass M originally at rest is subjected to a force whose direction is constant but magnitude varies with time according to the relation
$$F = {F_0}\left[ {1 - {{\left( {{{t - T} \over T}} \right)}^2}} \right]$$
Where F0 and T are constants. The force acts only for the time interval 2T. The velocity v of the particle after time 2T is :
$$F = {F_0}\left[ {1 - {{\left( {{{t - T} \over T}} \right)}^2}} \right]$$
Where F0 and T are constants. The force acts only for the time interval 2T. The velocity v of the particle after time 2T is :
18
The resistance of a conductor at 15$$^\circ$$C is 16$$\Omega$$ and at 100$$^\circ$$C is 20$$\Omega$$. What will be the temperature coefficient of resistance of the conductor?
19
In the given figure, two wheels P and Q are connected by a belt B. The radius of P is three times as that of Q. In case of same rotational kinetic energy, the ratio of rotational inertias $$\left( {{{{I_1}} \over {{I_2}}}} \right)$$ will be x : 1. The value of x will be _____________.


20
The difference in the number of waves when yellow light propagates through air and vacuum columns of the same thickness is one. The thickness of the air column is ___________ mm. [Refractive index of air = 1.0003, wavelength of yellow light in vacuum = 6000 $$\mathop A\limits^o $$]
21
In the given figure the magnetic flux through the loop increases according to the relation $$\phi$$B(t) = 10t2 + 20t, where $$\phi$$B is in milliwebers and t is in seconds.
The magnitude of current through R = 2$$\Omega$$ resistor at t = 5 s is ___________ mA.

The magnitude of current through R = 2$$\Omega$$ resistor at t = 5 s is ___________ mA.

22
A particle executes simple harmonic motion represented by displacement function as
x(t) = A sin($$\omega$$t + $$\phi$$)
If the position and velocity of the particle at t = 0 s are 2 cm and 2$$\omega$$ cm s$$-$$1 respectively, then its amplitude is $$x\sqrt 2 $$ cm where the value of x is _________________.
x(t) = A sin($$\omega$$t + $$\phi$$)
If the position and velocity of the particle at t = 0 s are 2 cm and 2$$\omega$$ cm s$$-$$1 respectively, then its amplitude is $$x\sqrt 2 $$ cm where the value of x is _________________.
23
A swimmer wants to cross a river from point A to point B. Line AB makes an angle of 30$$^\circ$$ with the flow of river. Magnitude of velocity of the swimmer is same as that of the river. The angle $$\theta$$ with the line AB should be _________$$^\circ$$, so that the swimmer reaches point B.


24
For the circuit shown, the value of current at time t = 3.2 s will be _________ A.

[Voltage distribution V(t) is shown by Fig. (1) and the circuit is shown in Fig. (2)]

[Voltage distribution V(t) is shown by Fig. (1) and the circuit is shown in Fig. (2)]
25
A small block slides down from the top of hemisphere of radius R = 3 m as shown in the figure. The height 'h' at which the block will lose contact with the surface of the sphere is __________ m.
(Assume there is no friction between the block and the hemisphere)
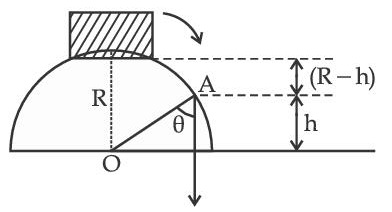
(Assume there is no friction between the block and the hemisphere)

26
The K$$\alpha$$ X-ray of molybdenum has wavelength 0.071 nm. If the energy of a molybdenum atoms with a K electron knocked out is 27.5 keV, the energy of this atom when an L electron is knocked out will be __________ keV. (Round off to the nearest integer)
[h = 4.14 $$\times$$ 10$$-$$15 eVs, c = 3 $$\times$$ 108 ms$$-$$1]
[h = 4.14 $$\times$$ 10$$-$$15 eVs, c = 3 $$\times$$ 108 ms$$-$$1]
27
The water is filled upto height of 12 m in a tank having vertical sidewalls. A hole is made in one of the walls at a depth 'h' below the water level. The value of 'h' for which the emerging steam of water strikes the ground at the maximum range is ________ m.