Chemistry
1
Deficiency of vitamin K causes :
2
In the following molecule,

Hybridisation of Carbon a, b, and c respectively are :

Hybridisation of Carbon a, b, and c respectively are :
3

Consider the given reaction, percentage yield of :
4
Given below are two statements :
Statement I : C2H5OH and AgCN both can generate nucleophile.
Statement II : KCN and AgCN both will generate nitrile nucleophile with all reaction conditions.
Choose the most appropriate option :
Statement I : C2H5OH and AgCN both can generate nucleophile.
Statement II : KCN and AgCN both will generate nitrile nucleophile with all reaction conditions.
Choose the most appropriate option :
5
The oxide that shows magnetic property is :
6
In the reaction of hypobromite with amide, the carbonyl carbon is lost as :
7
The secondary valency and the number of hydrogen bonded water molecule(s) in CuSO4 . 5H2O, respectively, are :
8
The first ionization energy of magnesium is smaller as compared to that of elements X and Y, but higher than that of Z. The elements X, Y and Z, respectively, are :
9
Given below are two statements :
Statement I : Bohr's theory accounts for the stability and line spectrum of Li+ ion.
Statement II : Bohr's theory was unable to explain the splitting of spectral lines in the presence of a magnetic field.
In the light of the above statements, choose the most appropriate answer from the options given below :
Statement I : Bohr's theory accounts for the stability and line spectrum of Li+ ion.
Statement II : Bohr's theory was unable to explain the splitting of spectral lines in the presence of a magnetic field.
In the light of the above statements, choose the most appropriate answer from the options given below :
10
The oxidation states of nitrogen in NO, NO2, N2O and NO$$_3^ - $$ are in the order of :
11
An organic compound "A" on treatment with benzene sulphonyl chloride gives compound B. B is soluble in dil. NaOH solution. Compound A is :
12
Main products formed during a reaction of 1-methoxy naphthalene with hydroiodic acid are :
13

Consider the above reaction, the product 'X' and 'Y' respectively are :
14
In Tollen's test for aldehyde, the overall number of electron(s) transferred to the Tollen's reagent formula [Ag(NH3)2]+ per aldehyde group to form silver mirror is ___________. (Round off to the Nearest Integer).
15
10.0 mL of Na2CO3 solution is titrated against 0.2 M HCl solution. The following titre values were obtained in 5 readings :
4.8 mL, 4.9 mL, 5.0 mL, 5.0 mL and 5.0 mL
Based on these readings, and convention of titrimetric estimation the concentration of Na2CO3 solution is ___________ mM.
(Round off to the Nearest Integer).
4.8 mL, 4.9 mL, 5.0 mL, 5.0 mL and 5.0 mL
Based on these readings, and convention of titrimetric estimation the concentration of Na2CO3 solution is ___________ mM.
(Round off to the Nearest Integer).
16
The number of species below that have two lone pairs of electrons in their central atom is _________. (Round off to the Nearest Integer).
SF4, BF$$_4^ - $$, ClF3, AsF3, PCl5, BrF5, XeF4, SF6
SF4, BF$$_4^ - $$, ClF3, AsF3, PCl5, BrF5, XeF4, SF6
17

Consider the above reaction where 6.1 g of Benzoic acid is used to get 7.8 g of m-bromo benzoic acid. The percentage yield of the product is __________
(Round off to the Nearest Integer).
[Given : Atomic masses : C : 12.0 u, H : 1.0 u, O : 16.0 u, Br : 80.0 u]
18
The molar conductivities at infinite dilution of barium chloride, sulphuric acid and hydrochloric acid are 280, 860 and 426 S cm2 mol$$-$$1 respectively. The molar conductivity at infinite dilution of barium sulphate is _________ S cm2 mol$$-$$1. (Round off to the Nearest Integer ).
19
The gas phase reaction $$2A(g) \rightleftharpoons {A_2}(g)$$ at 400 K has $$\Delta$$Go = + 25.2 kJ mol-1.
The equilibrium constant KC for this reaction is ________ $$\times$$ 10$$-$$2. (Round off to the Nearest Integer).
[Use : R = 8.3 J mol$$-$$1 K$$-$$1, ln 10 = 2.3 log10 2 = 0.30, 1 atm = 1 bar]
[antilog ($$-$$0.3) = 0.501]
The equilibrium constant KC for this reaction is ________ $$\times$$ 10$$-$$2. (Round off to the Nearest Integer).
[Use : R = 8.3 J mol$$-$$1 K$$-$$1, ln 10 = 2.3 log10 2 = 0.30, 1 atm = 1 bar]
[antilog ($$-$$0.3) = 0.501]
20
A reaction has a half life of 1 min. The time required for 99.9% completion of the reaction is _________ min. (Round off to the Nearest Integer). [Use : ln 2 = 0.69; ln 10 = 2.3]
21
The solubility of CdSO4 in water is 8.0 $$\times$$ 10$$-$$4 mol L$$-$$1. Its solubility in 0.01 M H2SO4 solution is __________ $$\times$$ 10$$-$$6 mol L$$-$$1. (Round off to the Nearest Integer). (Assume that solubility is much less than 0.01 M)
22
A solute A dimerizes in water. The boiling point of a 2 molal solution of A is 100.52$$^\circ$$C. The percentage association of A is __________. (Round off to the Nearest Integer).
[Use : Kb for water = 0.52 K kg mol$$-$$1 Boiling point of water = 100$$^\circ$$C]
[Use : Kb for water = 0.52 K kg mol$$-$$1 Boiling point of water = 100$$^\circ$$C]
Mathematics
1
Let y = y(x) be the solution of the differential equation
$${{dy} \over {dx}} = (y + 1)\left( {(y + 1){e^{{x^2}/2}} - x} \right)$$, 0 < x < 2.1, with y(2) = 0. Then the value of $${{dy} \over {dx}}$$ at x = 1 is equal to :
$${{dy} \over {dx}} = (y + 1)\left( {(y + 1){e^{{x^2}/2}} - x} \right)$$, 0 < x < 2.1, with y(2) = 0. Then the value of $${{dy} \over {dx}}$$ at x = 1 is equal to :
2
Let the system of linear equations
4x + $$\lambda$$y + 2z = 0
2x $$-$$ y + z = 0
$$\mu$$x + 2y + 3z = 0, $$\lambda$$, $$\mu$$$$\in$$R.
has a non-trivial solution. Then which of the following is true?
4x + $$\lambda$$y + 2z = 0
2x $$-$$ y + z = 0
$$\mu$$x + 2y + 3z = 0, $$\lambda$$, $$\mu$$$$\in$$R.
has a non-trivial solution. Then which of the following is true?
3
The area bounded by the curve 4y2 = x2(4 $$-$$ x)(x $$-$$ 2) is equal to :
4
If 15sin4$$\alpha$$ + 10cos4$$\alpha$$ = 6, for some $$\alpha$$$$\in$$R, then the value of
27sec6$$\alpha$$ + 8cosec6$$\alpha$$ is equal to :
27sec6$$\alpha$$ + 8cosec6$$\alpha$$ is equal to :
5
Let $$\overrightarrow a $$ and $$\overrightarrow b $$ be two non-zero vectors perpendicular to each other and $$|\overrightarrow a | = |\overrightarrow b |$$. If $$|\overrightarrow a \times \overrightarrow b | = |\overrightarrow a |$$, then the angle between the vectors $$\left( {\overrightarrow a + \overrightarrow b + \left( {\overrightarrow a \times \overrightarrow b } \right)} \right)$$ and $${\overrightarrow a }$$ is equal to :
6
Let a complex number be w = 1 $$-$$ $${\sqrt 3 }$$i. Let another complex number z be such that |zw| = 1 and arg(z) $$-$$ arg(w) = $${\pi \over 2}$$. Then the area of the triangle with vertices origin, z and w is equal to :
7
Let f : R $$ \to $$ R be a function defined as
$$f(x) = \left\{ \matrix{ {{\sin (a + 1)x + \sin 2x} \over {2x}},if\,x < 0 \hfill \cr b,\,if\,x\, = 0 \hfill \cr {{\sqrt {x + b{x^3}} - \sqrt x } \over {b{x^{5/2}}}},\,if\,x > 0 \hfill \cr} \right.$$
If f is continuous at x = 0, then the value of a + b is equal to :
$$f(x) = \left\{ \matrix{ {{\sin (a + 1)x + \sin 2x} \over {2x}},if\,x < 0 \hfill \cr b,\,if\,x\, = 0 \hfill \cr {{\sqrt {x + b{x^3}} - \sqrt x } \over {b{x^{5/2}}}},\,if\,x > 0 \hfill \cr} \right.$$
If f is continuous at x = 0, then the value of a + b is equal to :
8
Let g(x) = $$\int_0^x {f(t)dt} $$, where f is continuous function in [ 0, 3 ] such that $${1 \over 3}$$ $$ \le $$ f(t) $$ \le $$ 1 for all t$$\in$$ [0, 1] and 0 $$ \le $$ f(t) $$ \le $$ $${1 \over 2}$$ for all t$$\in$$ (1, 3]. The largest possible interval in which g(3) lies is :
9
Let in a series of 2n observations, half of them are equal to a and remaining half are equal to $$-$$a. Also by adding a constant b in each of these observations, the mean and standard deviation of new set become 5 and 20, respectively. Then the value of a2 + b2 is equal to :
10
In a triangle ABC, if $$|\overrightarrow {BC} | = 8,|\overrightarrow {CA} | = 7,|\overrightarrow {AB} | = 10$$, then the projection of the vector $$\overrightarrow {AB} $$ on $$\overrightarrow {AC} $$ is equal to :
11
Define a relation R over a class of n $$\times$$ n real matrices A and B as
"ARB iff there exists a non-singular matrix P such that PAP$$-$$1 = B".
Then which of the following is true?
"ARB iff there exists a non-singular matrix P such that PAP$$-$$1 = B".
Then which of the following is true?
12
Let the centroid of an equilateral triangle ABC be at the origin. Let one of the sides of the equilateral triangle be along the straight line x + y = 3. If R and r be the radius of circumcircle and incircle respectively of $$\Delta$$ABC, then (R + r) is equal to :
13
Let f : R $$-$$ {3} $$ \to $$ R $$-$$ {1} be defined by f(x) = $${{x - 2} \over {x - 3}}$$.
Let g : R $$ \to $$ R be given as g(x) = 2x $$-$$ 3. Then, the sum of all the values of x for which f$$-$$1(x) + g$$-$$1(x) = $${{13} \over 2}$$ is equal to :
Let g : R $$ \to $$ R be given as g(x) = 2x $$-$$ 3. Then, the sum of all the values of x for which f$$-$$1(x) + g$$-$$1(x) = $${{13} \over 2}$$ is equal to :
14
Let S1 be the sum of first 2n terms of an arithmetic progression. Let S2 be the sum of first 4n terms of the same arithmetic progression. If (S2 $$-$$ S1) is 1000, then the sum of the first 6n terms of the arithmetic progression is equal to :
15
If $$\sum\limits_{r = 1}^{10} {r!({r^3} + 6{r^2} + 2r + 5) = \alpha (11!)} $$, then the value of $$\alpha$$ is equal to ___________.
16
If f(x) and g(x) are two polynomials such that the polynomial P(x) = f(x3) + x g(x3) is divisible by x2 + x + 1, then P(1) is equal to ___________.
17
The term independent of x in the expansion of
$${\left[ {{{x + 1} \over {{x^{2/3}} - {x^{1/3}} + 1}} - {{x - 1} \over {x - {x^{1/2}}}}} \right]^{10}}$$, x $$\ne$$ 1, is equal to ____________.
$${\left[ {{{x + 1} \over {{x^{2/3}} - {x^{1/3}} + 1}} - {{x - 1} \over {x - {x^{1/2}}}}} \right]^{10}}$$, x $$\ne$$ 1, is equal to ____________.
18
Let y = y(x) be the solution of the differential equation
xdy $$-$$ ydx = $$\sqrt {({x^2} - {y^2})} dx$$, x $$ \ge $$ 1, with y(1) = 0. If the area bounded by the line x = 1, x = e$$\pi$$, y = 0 and y = y(x) is $$\alpha$$e2$$\pi$$ + $$\beta$$, then the value of 10($$\alpha$$ + $$\beta$$) is equal to __________.
xdy $$-$$ ydx = $$\sqrt {({x^2} - {y^2})} dx$$, x $$ \ge $$ 1, with y(1) = 0. If the area bounded by the line x = 1, x = e$$\pi$$, y = 0 and y = y(x) is $$\alpha$$e2$$\pi$$ + $$\beta$$, then the value of 10($$\alpha$$ + $$\beta$$) is equal to __________.
19
Let I be an identity matrix of order 2 $$\times$$ 2 and P = $$\left[ {\matrix{
2 & { - 1} \cr
5 & { - 3} \cr
} } \right]$$. Then the value of n$$\in$$N for which Pn = 5I $$-$$ 8P is equal to ____________.
20
Let f : R $$ \to $$ R satisfy the equation f(x + y) = f(x) . f(y) for all x, y $$\in$$R and f(x) $$\ne$$ 0 for any x$$\in$$R. If the function f is differentiable at x = 0 and f'(0) = 3, then
$$\mathop {\lim }\limits_{h \to 0} {1 \over h}(f(h) - 1)$$ is equal to ____________.
$$\mathop {\lim }\limits_{h \to 0} {1 \over h}(f(h) - 1)$$ is equal to ____________.
21
Let P(x) be a real polynomial of degree 3 which vanishes at x = $$-$$3. Let P(x) have local minima at x = 1, local maxima at x = $$-$$1 and $$\int\limits_{ - 1}^1 {P(x)dx} $$ = 18, then the sum of all the coefficients of the polynomial P(x) is equal to _________.
Physics
1
A plane electromagnetic wave propagating along y-direction can have the following pair of electric field $$\left( {\overrightarrow E } \right)$$ and magnetic field $$\left( {\overrightarrow B } \right)$$ components.
2
If the angular velocity of earth's spin is increased such that the bodies at the equator start floating, the duration of the day would be approximately : [Take g = 10 ms$$-$$2, the radius of earth, R = 6400 $$\times$$ 103 m, Take $$\pi$$ = 3.14]
3
An object of mass m1 collides with another object of mass m2, which is at rest. After the collision the objects move with equal speeds in opposite direction. The ratio of the masses m2 : m1 is :
4
In a series LCR circuit, the inductive reactance (XL) is 10$$\Omega$$ and the capacitive reactance (XC) is 4$$\Omega$$. The resistance (R) in the circuit is 6$$\Omega$$. The power factor of the circuit is :
5
A particle of mass m moves in a circular orbit under the central potential field, $$U(r) = - {C \over r}$$, where C is a positive constant. The correct radius $$-$$ velocity graph of the particle's motion is :
6
The angular momentum of a planet of mass M moving around the sun in an elliptical orbit is $${\overrightarrow L }$$. The magnitude of the areal velocity of the planet is :
7
Three rays of light, namely red (R), green (G) and blue (B) are incident on the face PQ of a right angled prism PQR as shown in the figure.

The refractive indices of the material of the prism for red, green and blue wavelength are 1.27, 1.42 and 1.49 respectively. The colour of the ray(s) emerging out of the face PR is :

The refractive indices of the material of the prism for red, green and blue wavelength are 1.27, 1.42 and 1.49 respectively. The colour of the ray(s) emerging out of the face PR is :
8
Consider a uniform wire of mass M and length L. It is bent into a semicircle. Its moment of inertia about a line perpendicular to the plane of the wire passing through the center is :
9
The velocity $$-$$ displacement graph of a particle is shown in the figure.
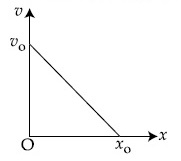
The acceleration $$-$$ displacement graph of the same particle is represented by :

The acceleration $$-$$ displacement graph of the same particle is represented by :
10
Consider a sample of oxygen behaving like an ideal gas. At 300 K, the ratio of root mean square (rms) velocity to the average velocity of gas molecule would be :
(Molecular weight of oxygen is 32g/mol; R = 8.3 J K$$-$$1 mol$$-$$1)
(Molecular weight of oxygen is 32g/mol; R = 8.3 J K$$-$$1 mol$$-$$1)
11
The time taken for the magnetic energy to reach 25% of its maximum value, when a solenoid of resistance R, inductance L is connected to a battery, is :
12
A solid cylinder of mass m is wrapped with an inextensible light string and, is placed on a rough inclined plane as shown in the figure. The frictional force acting between the cylinder and the inclined plane is :
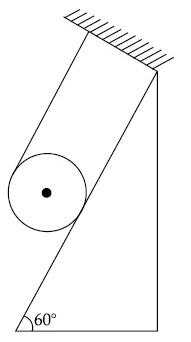
[The coefficient of static friction, $$\mu$$s' is 0.4]

[The coefficient of static friction, $$\mu$$s' is 0.4]
13
The function of time representing a simple harmonic motion with a period of $${\pi \over \omega }$$ is :
14
For an adiabatic expansion of an ideal gas, the fractional change in its pressure is equal to (where $$\gamma$$ is the ratio of specific heats) :
15
A proton and an $$\alpha$$-particle, having kinetic energies Kp and K$$\alpha$$ respectively, enter into a magnetic field at right angles.
The ratio of the radii of trajectory of proton to that of $$\alpha$$-particle is 2 : 1. The ratio of Kp : K$$\alpha$$ is :
The ratio of the radii of trajectory of proton to that of $$\alpha$$-particle is 2 : 1. The ratio of Kp : K$$\alpha$$ is :
16
An ideal gas in a cylinder is separated by a piston in such a way that the entropy of one part is S1 and that of the other part is S2. Given that S1 > S2. If the piston is removed then the total entropy of the system will be :
17
Which of the following statements are correct?
(A) Electric monopoles do not exist whereas magnetic monopoles exist.
(B) Magnetic field lines due to a solenoid at its ends and outside cannot be completely straight and confined.
(C) Magnetic field lines are completely confined within a toroid.
(D) Magnetic field lines inside a bar magnet are not parallel.
(E) $$\chi $$ = $$-$$1 is the condition for a perfect diamagnetic material, where x is its magnetic susceptibility.
Choose the correct answer from the options given below :
(A) Electric monopoles do not exist whereas magnetic monopoles exist.
(B) Magnetic field lines due to a solenoid at its ends and outside cannot be completely straight and confined.
(C) Magnetic field lines are completely confined within a toroid.
(D) Magnetic field lines inside a bar magnet are not parallel.
(E) $$\chi $$ = $$-$$1 is the condition for a perfect diamagnetic material, where x is its magnetic susceptibility.
Choose the correct answer from the options given below :
18
Two wires of same length and thickness having specific resistances 6$$\Omega$$ cm and 3$$\Omega$$ cm respectively are connected in parallel. The effective resistivity is $$\rho$$$$\Omega$$ cm. The value of $$\rho$$, to the nearest integer, is ____________.
19
Consider a 72 cm long wire AB as shown in the figure. The galvanometer jockey is placed at P on AB at a distance x cm from A. The galvanometer shows zero deflection.

The value of x, to the nearest integer, is ___________.

The value of x, to the nearest integer, is ___________.
20
A galaxy is moving away from the earth at a speed of 286 kms$$-$$1. The shift in the wavelength of a redline at 630 nm is x $$\times$$ 10$$-$$10 m. The value of x, to the nearest integer, is ____________. [Take the value of speed of light c, as 3 $$\times$$ 108 ms$$-$$1]
21
A ball of mass 4 kg, moving with a velocity of 10 ms$$-$$1, collides with a spring of length 8 m and force constant 100 Nm$$-$$1. The length of the compressed spring is x m. The value of x, to the nearest integer, is ____________.
22
Consider a water tank as shown in the figure. It's cross-sectional area is 0.4 m2. The tank has an opening B near the bottom whose cross-section area is 1 cm2. A load of 24 kg is applied on the water at the top when the height of the water level is 40 cm above the bottom, the velocity of water coming out the opening B is v ms-1.
The value of v, to the nearest integer, is ___________. [Take value of g to be 10 ms-2]
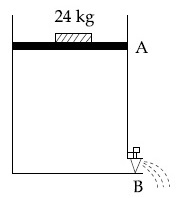
The value of v, to the nearest integer, is ___________. [Take value of g to be 10 ms-2]

23
The radius of a sphere is measured to be (7.50 $$\pm$$ 0.85) cm. Suppose the percentage error in its volume is x.
The value of x, to the nearest x, is __________.
The value of x, to the nearest x, is __________.
24
The projectile motion of a particle of mass 5 g is shown in the figure.

The initial velocity of the particle is $$5\sqrt 2 $$ ms-1 and the air resistance is assumed to be negligible. The magnitude of the change in momentum between the points A and B is x $$\times$$ 10-2 kgms-1. The value of x, to the nearest integer, is __________.

The initial velocity of the particle is $$5\sqrt 2 $$ ms-1 and the air resistance is assumed to be negligible. The magnitude of the change in momentum between the points A and B is x $$\times$$ 10-2 kgms-1. The value of x, to the nearest integer, is __________.
25
An infinite number of point charges, each carrying 1 $$\mu$$C charge, are placed along the y-axis at y = 1 m, 2 m, 4 m, 8 m ...............
The total force on a 1C point charge, placed at the origin, is x $$\times$$ 103 N.
The value of x, to the nearest integer, is __________. [Take $${1 \over {4\pi {\varepsilon _0}}} = 9 \times {10^9}$$ Nm2/C2]
The total force on a 1C point charge, placed at the origin, is x $$\times$$ 103 N.
The value of x, to the nearest integer, is __________. [Take $${1 \over {4\pi {\varepsilon _0}}} = 9 \times {10^9}$$ Nm2/C2]
1
JEE Main 2021 (Online) 18th March Evening Shift
Numerical
+4
-1
A ball of mass 4 kg, moving with a velocity of 10 ms$$-$$1, collides with a spring of length 8 m and force constant 100 Nm$$-$$1. The length of the compressed spring is x m. The value of x, to the nearest integer, is ____________.
Your input ____
2
JEE Main 2021 (Online) 18th March Evening Shift
Numerical
+4
-1
Consider a water tank as shown in the figure. It's cross-sectional area is 0.4 m2. The tank has an opening B near the bottom whose cross-section area is 1 cm2. A load of 24 kg is applied on the water at the top when the height of the water level is 40 cm above the bottom, the velocity of water coming out the opening B is v ms-1.
The value of v, to the nearest integer, is ___________. [Take value of g to be 10 ms-2]

The value of v, to the nearest integer, is ___________. [Take value of g to be 10 ms-2]

Your input ____
3
JEE Main 2021 (Online) 18th March Evening Shift
Numerical
+4
-1
The radius of a sphere is measured to be (7.50 $$\pm$$ 0.85) cm. Suppose the percentage error in its volume is x.
The value of x, to the nearest x, is __________.
The value of x, to the nearest x, is __________.
Your input ____
4
JEE Main 2021 (Online) 18th March Evening Shift
Numerical
+4
-1
The projectile motion of a particle of mass 5 g is shown in the figure.

The initial velocity of the particle is $$5\sqrt 2 $$ ms-1 and the air resistance is assumed to be negligible. The magnitude of the change in momentum between the points A and B is x $$\times$$ 10-2 kgms-1. The value of x, to the nearest integer, is __________.

The initial velocity of the particle is $$5\sqrt 2 $$ ms-1 and the air resistance is assumed to be negligible. The magnitude of the change in momentum between the points A and B is x $$\times$$ 10-2 kgms-1. The value of x, to the nearest integer, is __________.
Your input ____
Subject
Chemistry
22
Mathematics
21
Physics
25
More Papers of JEE Main
2025
JEE Main 2025 (Online) 8th April Evening ShiftJEE Main 2025 (Online) 7th April Evening ShiftJEE Main 2025 (Online) 7th April Morning ShiftJEE Main 2025 (Online) 4th April Evening ShiftJEE Main 2025 (Online) 4th April Morning ShiftJEE Main 2025 (Online) 3rd April Evening ShiftJEE Main 2025 (Online) 3rd April Morning ShiftJEE Main 2025 (Online) 2nd April Evening ShiftJEE Main 2025 (Online) 2nd April Morning ShiftJEE Main 2025 (Online) 29th January Evening ShiftJEE Main 2025 (Online) 29th January Morning ShiftJEE Main 2025 (Online) 28th January Evening ShiftJEE Main 2025 (Online) 28th January Morning ShiftJEE Main 2025 (Online) 24th January Evening ShiftJEE Main 2025 (Online) 24th January Morning ShiftJEE Main 2025 (Online) 23rd January Evening ShiftJEE Main 2025 (Online) 23rd January Morning ShiftJEE Main 2025 (Online) 22nd January Evening ShiftJEE Main 2025 (Online) 22nd January Morning Shift2024
JEE Main 2024 (Online) 9th April Evening ShiftJEE Main 2024 (Online) 9th April Morning ShiftJEE Main 2024 (Online) 8th April Evening ShiftJEE Main 2024 (Online) 8th April Morning ShiftJEE Main 2024 (Online) 6th April Evening ShiftJEE Main 2024 (Online) 6th April Morning ShiftJEE Main 2024 (Online) 5th April Evening ShiftJEE Main 2024 (Online) 5th April Morning ShiftJEE Main 2024 (Online) 4th April Evening ShiftJEE Main 2024 (Online) 4th April Morning ShiftJEE Main 2024 (Online) 1st February Evening ShiftJEE Main 2024 (Online) 1st February Morning ShiftJEE Main 2024 (Online) 31st January Evening ShiftJEE Main 2024 (Online) 31st January Morning ShiftJEE Main 2024 (Online) 30th January Evening ShiftJEE Main 2024 (Online) 30th January Morning ShiftJEE Main 2024 (Online) 29th January Evening ShiftJEE Main 2024 (Online) 29th January Morning ShiftJEE Main 2024 (Online) 27th January Evening ShiftJEE Main 2024 (Online) 27th January Morning Shift2023
JEE Main 2023 (Online) 15th April Morning ShiftJEE Main 2023 (Online) 13th April Evening ShiftJEE Main 2023 (Online) 13th April Morning ShiftJEE Main 2023 (Online) 12th April Morning ShiftJEE Main 2023 (Online) 11th April Evening ShiftJEE Main 2023 (Online) 11th April Morning ShiftJEE Main 2023 (Online) 10th April Evening ShiftJEE Main 2023 (Online) 10th April Morning ShiftJEE Main 2023 (Online) 8th April Evening ShiftJEE Main 2023 (Online) 8th April Morning ShiftJEE Main 2023 (Online) 6th April Evening ShiftJEE Main 2023 (Online) 6th April Morning ShiftJEE Main 2023 (Online) 1st February Evening ShiftJEE Main 2023 (Online) 1st February Morning ShiftJEE Main 2023 (Online) 31st January Evening ShiftJEE Main 2023 (Online) 31st January Morning ShiftJEE Main 2023 (Online) 30th January Evening ShiftJEE Main 2023 (Online) 30th January Morning ShiftJEE Main 2023 (Online) 29th January Evening ShiftJEE Main 2023 (Online) 29th January Morning ShiftJEE Main 2023 (Online) 25th January Evening ShiftJEE Main 2023 (Online) 25th January Morning ShiftJEE Main 2023 (Online) 24th January Evening ShiftJEE Main 2023 (Online) 24th January Morning Shift2022
JEE Main 2022 (Online) 29th July Evening ShiftJEE Main 2022 (Online) 29th July Morning ShiftJEE Main 2022 (Online) 28th July Evening ShiftJEE Main 2022 (Online) 28th July Morning ShiftJEE Main 2022 (Online) 27th July Evening ShiftJEE Main 2022 (Online) 27th July Morning ShiftJEE Main 2022 (Online) 26th July Evening ShiftJEE Main 2022 (Online) 26th July Morning ShiftJEE Main 2022 (Online) 25th July Evening ShiftJEE Main 2022 (Online) 25th July Morning ShiftJEE Main 2022 (Online) 30th June Morning ShiftJEE Main 2022 (Online) 29th June Evening ShiftJEE Main 2022 (Online) 29th June Morning ShiftJEE Main 2022 (Online) 28th June Evening ShiftJEE Main 2022 (Online) 28th June Morning ShiftJEE Main 2022 (Online) 27th June Evening ShiftJEE Main 2022 (Online) 27th June Morning ShiftJEE Main 2022 (Online) 26th June Evening ShiftJEE Main 2022 (Online) 26th June Morning ShiftJEE Main 2022 (Online) 25th June Evening ShiftJEE Main 2022 (Online) 25th June Morning ShiftJEE Main 2022 (Online) 24th June Evening ShiftJEE Main 2022 (Online) 24th June Morning Shift2021
JEE Main 2021 (Online) 1st September Evening ShiftJEE Main 2021 (Online) 31st August Evening ShiftJEE Main 2021 (Online) 31st August Morning ShiftJEE Main 2021 (Online) 27th August Evening ShiftJEE Main 2021 (Online) 27th August Morning ShiftJEE Main 2021 (Online) 26th August Evening ShiftJEE Main 2021 (Online) 26th August Morning ShiftJEE Main 2021 (Online) 27th July Evening ShiftJEE Main 2021 (Online) 27th July Morning ShiftJEE Main 2021 (Online) 25th July Evening ShiftJEE Main 2021 (Online) 25th July Morning ShiftJEE Main 2021 (Online) 22th July Evening ShiftJEE Main 2021 (Online) 20th July Evening ShiftJEE Main 2021 (Online) 20th July Morning ShiftJEE Main 2021 (Online) 18th March Evening ShiftJEE Main 2021 (Online) 18th March Morning ShiftJEE Main 2021 (Online) 17th March Evening ShiftJEE Main 2021 (Online) 17th March Morning ShiftJEE Main 2021 (Online) 16th March Evening ShiftJEE Main 2021 (Online) 16th March Morning ShiftJEE Main 2021 (Online) 26th February Evening ShiftJEE Main 2021 (Online) 26th February Morning ShiftJEE Main 2021 (Online) 25th February Evening ShiftJEE Main 2021 (Online) 25th February Morning ShiftJEE Main 2021 (Online) 24th February Evening ShiftJEE Main 2021 (Online) 24th February Morning Shift2020
JEE Main 2020 (Online) 6th September Evening SlotJEE Main 2020 (Online) 6th September Morning SlotJEE Main 2020 (Online) 5th September Evening SlotJEE Main 2020 (Online) 5th September Morning SlotJEE Main 2020 (Online) 4th September Evening SlotJEE Main 2020 (Online) 4th September Morning SlotJEE Main 2020 (Online) 3rd September Evening SlotJEE Main 2020 (Online) 3rd September Morning SlotJEE Main 2020 (Online) 2nd September Evening SlotJEE Main 2020 (Online) 2nd September Morning SlotJEE Main 2020 (Online) 9th January Evening SlotJEE Main 2020 (Online) 9th January Morning SlotJEE Main 2020 (Online) 8th January Evening SlotJEE Main 2020 (Online) 8th January Morning SlotJEE Main 2020 (Online) 7th January Evening SlotJEE Main 2020 (Online) 7th January Morning Slot2019
JEE Main 2019 (Online) 12th April Evening SlotJEE Main 2019 (Online) 12th April Morning SlotJEE Main 2019 (Online) 10th April Evening SlotJEE Main 2019 (Online) 10th April Morning SlotJEE Main 2019 (Online) 9th April Evening SlotJEE Main 2019 (Online) 9th April Morning SlotJEE Main 2019 (Online) 8th April Evening SlotJEE Main 2019 (Online) 8th April Morning SlotJEE Main 2019 (Online) 12th January Evening SlotJEE Main 2019 (Online) 12th January Morning SlotJEE Main 2019 (Online) 11th January Evening SlotJEE Main 2019 (Online) 11th January Morning SlotJEE Main 2019 (Online) 10th January Evening SlotJEE Main 2019 (Online) 10th January Morning SlotJEE Main 2019 (Online) 9th January Evening SlotJEE Main 2019 (Online) 9th January Morning Slot2018
JEE Main 2018 (Online) 16th April Morning SlotJEE Main 2018 (Offline)JEE Main 2018 (Online) 15th April Evening SlotJEE Main 2018 (Online) 15th April Morning Slot2017
JEE Main 2017 (Online) 9th April Morning SlotJEE Main 2017 (Online) 8th April Morning SlotJEE Main 2017 (Offline)2016
JEE Main 2016 (Online) 10th April Morning SlotJEE Main 2016 (Online) 9th April Morning SlotJEE Main 2016 (Offline)2015
JEE Main 2015 (Offline)2014
JEE Main 2014 (Offline)2013
JEE Main 2013 (Offline)2012
AIEEE 20122011
AIEEE 20112010
AIEEE 20102009
AIEEE 20092008
AIEEE 20082007
AIEEE 20072006
AIEEE 20062005
AIEEE 20052004
AIEEE 20042003
AIEEE 20032002
AIEEE 2002