2025
JEE Main 2025 (Online) 8th April Evening ShiftJEE Main 2025 (Online) 7th April Evening ShiftJEE Main 2025 (Online) 7th April Morning ShiftJEE Main 2025 (Online) 4th April Evening ShiftJEE Main 2025 (Online) 4th April Morning ShiftJEE Main 2025 (Online) 3rd April Evening ShiftJEE Main 2025 (Online) 3rd April Morning ShiftJEE Main 2025 (Online) 2nd April Evening ShiftJEE Main 2025 (Online) 2nd April Morning ShiftJEE Main 2025 (Online) 29th January Evening ShiftJEE Main 2025 (Online) 29th January Morning ShiftJEE Main 2025 (Online) 28th January Evening ShiftJEE Main 2025 (Online) 28th January Morning ShiftJEE Main 2025 (Online) 24th January Evening ShiftJEE Main 2025 (Online) 24th January Morning ShiftJEE Main 2025 (Online) 23rd January Evening ShiftJEE Main 2025 (Online) 23rd January Morning ShiftJEE Main 2025 (Online) 22nd January Evening ShiftJEE Main 2025 (Online) 22nd January Morning Shift2024
JEE Main 2024 (Online) 9th April Evening ShiftJEE Main 2024 (Online) 9th April Morning ShiftJEE Main 2024 (Online) 8th April Evening ShiftJEE Main 2024 (Online) 8th April Morning ShiftJEE Main 2024 (Online) 6th April Evening ShiftJEE Main 2024 (Online) 6th April Morning ShiftJEE Main 2024 (Online) 5th April Evening ShiftJEE Main 2024 (Online) 5th April Morning ShiftJEE Main 2024 (Online) 4th April Evening ShiftJEE Main 2024 (Online) 4th April Morning ShiftJEE Main 2024 (Online) 1st February Evening ShiftJEE Main 2024 (Online) 1st February Morning ShiftJEE Main 2024 (Online) 31st January Evening ShiftJEE Main 2024 (Online) 31st January Morning ShiftJEE Main 2024 (Online) 30th January Evening ShiftJEE Main 2024 (Online) 30th January Morning ShiftJEE Main 2024 (Online) 29th January Evening ShiftJEE Main 2024 (Online) 29th January Morning ShiftJEE Main 2024 (Online) 27th January Evening ShiftJEE Main 2024 (Online) 27th January Morning Shift2023
JEE Main 2023 (Online) 15th April Morning ShiftJEE Main 2023 (Online) 13th April Evening ShiftJEE Main 2023 (Online) 13th April Morning ShiftJEE Main 2023 (Online) 12th April Morning ShiftJEE Main 2023 (Online) 11th April Evening ShiftJEE Main 2023 (Online) 11th April Morning ShiftJEE Main 2023 (Online) 10th April Evening ShiftJEE Main 2023 (Online) 10th April Morning ShiftJEE Main 2023 (Online) 8th April Evening ShiftJEE Main 2023 (Online) 8th April Morning ShiftJEE Main 2023 (Online) 6th April Evening ShiftJEE Main 2023 (Online) 6th April Morning ShiftJEE Main 2023 (Online) 1st February Evening ShiftJEE Main 2023 (Online) 1st February Morning ShiftJEE Main 2023 (Online) 31st January Evening ShiftJEE Main 2023 (Online) 31st January Morning ShiftJEE Main 2023 (Online) 30th January Evening ShiftJEE Main 2023 (Online) 30th January Morning ShiftJEE Main 2023 (Online) 29th January Evening ShiftJEE Main 2023 (Online) 29th January Morning ShiftJEE Main 2023 (Online) 25th January Evening ShiftJEE Main 2023 (Online) 25th January Morning ShiftJEE Main 2023 (Online) 24th January Evening ShiftJEE Main 2023 (Online) 24th January Morning Shift2022
JEE Main 2022 (Online) 29th July Evening ShiftJEE Main 2022 (Online) 29th July Morning ShiftJEE Main 2022 (Online) 28th July Evening ShiftJEE Main 2022 (Online) 28th July Morning ShiftJEE Main 2022 (Online) 27th July Evening ShiftJEE Main 2022 (Online) 27th July Morning ShiftJEE Main 2022 (Online) 26th July Evening ShiftJEE Main 2022 (Online) 26th July Morning ShiftJEE Main 2022 (Online) 25th July Evening ShiftJEE Main 2022 (Online) 25th July Morning ShiftJEE Main 2022 (Online) 30th June Morning ShiftJEE Main 2022 (Online) 29th June Evening ShiftJEE Main 2022 (Online) 29th June Morning ShiftJEE Main 2022 (Online) 28th June Evening ShiftJEE Main 2022 (Online) 28th June Morning ShiftJEE Main 2022 (Online) 27th June Evening ShiftJEE Main 2022 (Online) 27th June Morning ShiftJEE Main 2022 (Online) 26th June Evening ShiftJEE Main 2022 (Online) 26th June Morning ShiftJEE Main 2022 (Online) 25th June Evening ShiftJEE Main 2022 (Online) 25th June Morning ShiftJEE Main 2022 (Online) 24th June Evening ShiftJEE Main 2022 (Online) 24th June Morning Shift2021
JEE Main 2021 (Online) 1st September Evening ShiftJEE Main 2021 (Online) 31st August Evening ShiftJEE Main 2021 (Online) 31st August Morning ShiftJEE Main 2021 (Online) 27th August Evening ShiftJEE Main 2021 (Online) 27th August Morning ShiftJEE Main 2021 (Online) 26th August Evening ShiftJEE Main 2021 (Online) 26th August Morning ShiftJEE Main 2021 (Online) 27th July Evening ShiftJEE Main 2021 (Online) 27th July Morning ShiftJEE Main 2021 (Online) 25th July Evening ShiftJEE Main 2021 (Online) 25th July Morning ShiftJEE Main 2021 (Online) 22th July Evening ShiftJEE Main 2021 (Online) 20th July Evening ShiftJEE Main 2021 (Online) 20th July Morning ShiftJEE Main 2021 (Online) 18th March Evening ShiftJEE Main 2021 (Online) 18th March Morning ShiftJEE Main 2021 (Online) 17th March Evening ShiftJEE Main 2021 (Online) 17th March Morning ShiftJEE Main 2021 (Online) 16th March Evening ShiftJEE Main 2021 (Online) 16th March Morning ShiftJEE Main 2021 (Online) 26th February Evening ShiftJEE Main 2021 (Online) 26th February Morning ShiftJEE Main 2021 (Online) 25th February Evening ShiftJEE Main 2021 (Online) 25th February Morning ShiftJEE Main 2021 (Online) 24th February Evening ShiftJEE Main 2021 (Online) 24th February Morning Shift2020
JEE Main 2020 (Online) 6th September Evening SlotJEE Main 2020 (Online) 6th September Morning SlotJEE Main 2020 (Online) 5th September Evening SlotJEE Main 2020 (Online) 5th September Morning SlotJEE Main 2020 (Online) 4th September Evening SlotJEE Main 2020 (Online) 4th September Morning SlotJEE Main 2020 (Online) 3rd September Evening SlotJEE Main 2020 (Online) 3rd September Morning SlotJEE Main 2020 (Online) 2nd September Evening SlotJEE Main 2020 (Online) 2nd September Morning SlotJEE Main 2020 (Online) 9th January Evening SlotJEE Main 2020 (Online) 9th January Morning SlotJEE Main 2020 (Online) 8th January Evening SlotJEE Main 2020 (Online) 8th January Morning SlotJEE Main 2020 (Online) 7th January Evening SlotJEE Main 2020 (Online) 7th January Morning Slot2019
JEE Main 2019 (Online) 12th April Evening SlotJEE Main 2019 (Online) 12th April Morning SlotJEE Main 2019 (Online) 10th April Evening SlotJEE Main 2019 (Online) 10th April Morning SlotJEE Main 2019 (Online) 9th April Evening SlotJEE Main 2019 (Online) 9th April Morning SlotJEE Main 2019 (Online) 8th April Evening SlotJEE Main 2019 (Online) 8th April Morning SlotJEE Main 2019 (Online) 12th January Evening SlotJEE Main 2019 (Online) 12th January Morning SlotJEE Main 2019 (Online) 11th January Evening SlotJEE Main 2019 (Online) 11th January Morning SlotJEE Main 2019 (Online) 10th January Evening SlotJEE Main 2019 (Online) 10th January Morning SlotJEE Main 2019 (Online) 9th January Evening SlotJEE Main 2019 (Online) 9th January Morning Slot2018
JEE Main 2018 (Online) 16th April Morning SlotJEE Main 2018 (Offline)JEE Main 2018 (Online) 15th April Evening SlotJEE Main 2018 (Online) 15th April Morning Slot2017
JEE Main 2017 (Online) 9th April Morning SlotJEE Main 2017 (Online) 8th April Morning SlotJEE Main 2017 (Offline)2016
JEE Main 2016 (Online) 10th April Morning SlotJEE Main 2016 (Online) 9th April Morning SlotJEE Main 2016 (Offline)2015
JEE Main 2015 (Offline)2014
JEE Main 2014 (Offline)2013
JEE Main 2013 (Offline)2012
AIEEE 20122011
AIEEE 20112010
AIEEE 20102009
AIEEE 20092008
AIEEE 20082007
AIEEE 20072006
AIEEE 20062005
AIEEE 20052004
AIEEE 20042003
AIEEE 20032002
AIEEE 2002JEE Main 2020 (Online) 9th January Evening Slot
Paper was held on Thu, Jan 9, 2020 9:30 AM
Chemistry
1
Which of the following reactions will not
produce a racemic product?
2
In the following reaction A is :
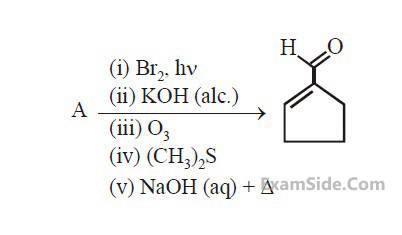

3
The first and second ionisation enthalpies of a
metal are 496 and 4560 kJ mol–1, respectively.
How many moles of HCl and H2SO4,
respectively, will be needed to react completely
with 1 mole of the metal hydroxide ?
4
Consider the following reactions,
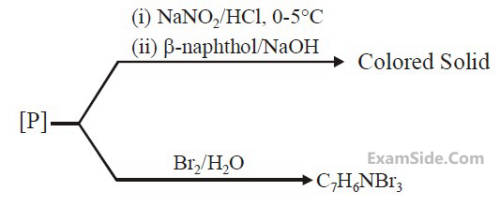
The compound [P] is :

The compound [P] is :
5
Consider the following reactions
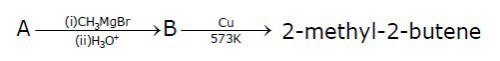
The mass percentage of carbon in A is ______.
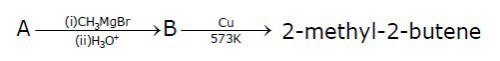
The mass percentage of carbon in A is ______.
6
10.30 mg of O2 is dissolved into a liter of sea
water of density 1.03 g/mL. The concentration
of O2 in ppm is__________.
7
The sum of the total number of bonds between
chromium and oxygen atoms in chromate and
dichromate ions is ____________.
8
A sample of milk splits after 60 min. at 300 K
and after 40 min. at 400 K when the population
of lactobacillus acidophilus in it doubles. The
activa tion energy (in kJ/ mol) for this process
is closest to__________.
(Given, R = 8.3 J mol–1 K–1, $$\ln \left( {{3 \over 2}} \right) = 0.4$$, e–3 = 4.0)
(Given, R = 8.3 J mol–1 K–1, $$\ln \left( {{3 \over 2}} \right) = 0.4$$, e–3 = 4.0)
9
A cylinder containing an ideal gas (0.1 mol of
1.0 dm3) is in thermal equilibrium with a large
volume of 0.5 molal aqueous solution of
ethylene glycol at its freezing point. If the
stoppers S1 and S2 (as shown in the figure) are
suddenly withdrawn, the volume of the gas in
litres after equilibrium is achieved will be____.
(Given, Kf (water) = 2.0 K kg mol–1,
R = 0.08 dm3 atm K–1 mol–1)
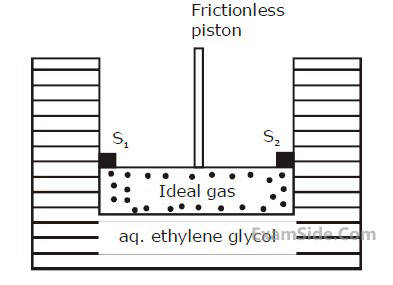
(Given, Kf (water) = 2.0 K kg mol–1,
R = 0.08 dm3 atm K–1 mol–1)

10
The true statement amongst the following is :
11
The number of sp2 hybrid orbitals in a molecule
of benzene is :
12
The isomer(s) of [Co(NH3)4Cl2] that has/have
a Cl–Co–Cl angle of 90°, is/are :
13
The reaction of H3N3B3Cl3 (A) with LiBH4 in
tetrahydrofuran gives inorganic benzene (B).
Further, the reaction of (A) with (C) leads to
H3N3B3(Me)3. Compounds (B) and (C)
respectively, are :
14
A, B and C are three biomolecules. The results
of the tests performed on them are given
below:
$$ \begin{array}{|l|l|l|l|} \hline & \begin{array}{l} \text { Molisch's } \\ \text { Test } \end{array} & \begin{array}{l} \text { Barfoed } \\ \text { Test } \end{array} & \begin{array}{l} \text { Biuret } \\ \text { Test } \end{array} \\ \hline \text { A } & \text { Positive } & \text { Negative } & \text { Negative } \\ \hline \text { B } & \text { Positive } & \text { Positive } & \text { Negative } \\ \hline \text { C } & \text { Negative } & \text { Negative } & \text { Positive } \\ \hline \end{array} $$
A, B and C are respectively :
$$ \begin{array}{|l|l|l|l|} \hline & \begin{array}{l} \text { Molisch's } \\ \text { Test } \end{array} & \begin{array}{l} \text { Barfoed } \\ \text { Test } \end{array} & \begin{array}{l} \text { Biuret } \\ \text { Test } \end{array} \\ \hline \text { A } & \text { Positive } & \text { Negative } & \text { Negative } \\ \hline \text { B } & \text { Positive } & \text { Positive } & \text { Negative } \\ \hline \text { C } & \text { Negative } & \text { Negative } & \text { Positive } \\ \hline \end{array} $$
A, B and C are respectively :
15
5 g of zinc is treated separately with an excess
of
(a) dilute hydrochloric acid and
(b) aqueous sodium hydroxide.
The ratio of the volumes of H2 evolved in these two reactions is :
(a) dilute hydrochloric acid and
(b) aqueous sodium hydroxide.
The ratio of the volumes of H2 evolved in these two reactions is :
16
The solubility product of Cr(OH)3 at 298 K is
6.0 × 10–31. The concentration of hydroxide ions
in a saturated solution of Cr(OH)3 will be :
17
The decreasing order of basicity of the
following amines is :
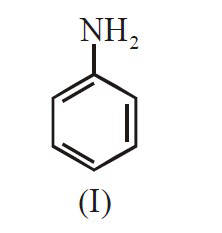
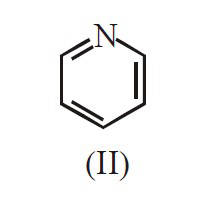

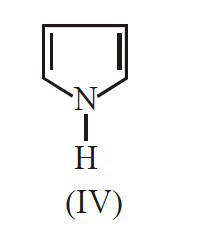




18
In the figure shown below reactant A
(represented by square) is in equilibrium with
product B (represented by circle). The
equilibrium constant is :
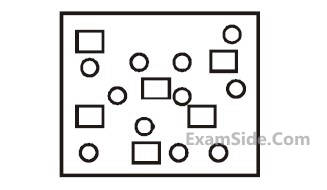

19
Which of the following has the shortest C-Cl
bond?
20
The correct order of the spin-only magnetic
moments of the following complexes is :
(I) [Cr(H2O)6]Br2
(II) Na4[Fe(CN)6]
(III) Na3[Fe(C2O4)3] ($$\Delta $$0 $$>$$ P)
(IV) (Et4N)2[CoCl4]
(I) [Cr(H2O)6]Br2
(II) Na4[Fe(CN)6]
(III) Na3[Fe(C2O4)3] ($$\Delta $$0 $$>$$ P)
(IV) (Et4N)2[CoCl4]
Mathematics
1
Let ƒ and g be differentiable functions on R
such that fog is the identity function. If for some
a, b $$ \in $$ R, g'(a) = 5 and g(a) = b, then ƒ'(b) is
equal to :
2
In the expansion of $${\left( {{x \over {\cos \theta }} + {1 \over {x\sin \theta }}} \right)^{16}}$$, if $${\ell _1}$$ is
the least value of the term independent of x
when $${\pi \over 8} \le \theta \le {\pi \over 4}$$ and $${\ell _2}$$ is the least value of the
term independent of x when $${\pi \over {16}} \le \theta \le {\pi \over 8}$$, then
the ratio $${\ell _2}$$ : $${\ell _1}$$ is equal to :
3
Let a – 2b + c = 1.
If $$f(x)=\left| {\matrix{ {x + a} & {x + 2} & {x + 1} \cr {x + b} & {x + 3} & {x + 2} \cr {x + c} & {x + 4} & {x + 3} \cr } } \right|$$, then:
If $$f(x)=\left| {\matrix{ {x + a} & {x + 2} & {x + 1} \cr {x + b} & {x + 3} & {x + 2} \cr {x + c} & {x + 4} & {x + 3} \cr } } \right|$$, then:
4
If z be a complex number satisfying
|Re(z)| + |Im(z)| = 4, then |z| cannot be :
5
If $$\int {{{d\theta } \over {{{\cos }^2}\theta \left( {\tan 2\theta + \sec 2\theta } \right)}}} = \lambda \tan \theta + 2{\log _e}\left| {f\left( \theta \right)} \right| + C$$
where C is a constant of integration, then the ordered pair ($$\lambda $$, ƒ($$\theta $$)) is equal to :
where C is a constant of integration, then the ordered pair ($$\lambda $$, ƒ($$\theta $$)) is equal to :
6
If $${{dy} \over {dx}} = {{xy} \over {{x^2} + {y^2}}}$$; y(1) = 1; then a value of x
satisfying y(x) = e is :
7
Let a function ƒ : [0, 5] $$ \to $$ R be continuous,
ƒ(1) = 3 and F be defined as :
$$F(x) = \int\limits_1^x {{t^2}g(t)dt} $$ , where $$g(t) = \int\limits_1^t {f(u)du} $$
Then for the function F, the point x = 1 is :
$$F(x) = \int\limits_1^x {{t^2}g(t)dt} $$ , where $$g(t) = \int\limits_1^t {f(u)du} $$
Then for the function F, the point x = 1 is :
8
If 10 different balls are to be placed in 4 distinct
boxes at random, then the probability that two
of these boxes contain exactly 2 and 3 balls is :
9
Let an be the nth term of a G.P. of positive terms.
$$\sum\limits_{n = 1}^{100} {{a_{2n + 1}} = 200} $$ and $$\sum\limits_{n = 1}^{100} {{a_{2n}} = 100} $$,
then $$\sum\limits_{n = 1}^{200} {{a_n}} $$ is equal to :
$$\sum\limits_{n = 1}^{100} {{a_{2n + 1}} = 200} $$ and $$\sum\limits_{n = 1}^{100} {{a_{2n}} = 100} $$,
then $$\sum\limits_{n = 1}^{200} {{a_n}} $$ is equal to :
10
If A = {x $$ \in $$ R : |x| < 2} and B = {x $$ \in $$ R : |x – 2| $$ \ge $$ 3};
then :
11
If $$x = \sum\limits_{n = 0}^\infty {{{\left( { - 1} \right)}^n}{{\tan }^{2n}}\theta } $$ and $$y = \sum\limits_{n = 0}^\infty {{{\cos }^{2n}}\theta } $$
for 0 < $$\theta $$ < $${\pi \over 4}$$, then :
for 0 < $$\theta $$ < $${\pi \over 4}$$, then :
12
Given : $$f(x) = \left\{ {\matrix{
{x\,\,\,\,\,,} & {0 \le x < {1 \over 2}} \cr
{{1 \over 2}\,\,\,\,,} & {x = {1 \over 2}} \cr
{1 - x\,\,\,,} & {{1 \over 2} < x \le 1} \cr
} } \right.$$
and $$g(x) = \left( {x - {1 \over 2}} \right)^2,x \in R$$
Then the area (in sq. units) of the region bounded by the curves, y = ƒ(x) and y = g(x) between the lines, 2x = 1 and 2x = $$\sqrt 3 $$, is :
and $$g(x) = \left( {x - {1 \over 2}} \right)^2,x \in R$$
Then the area (in sq. units) of the region bounded by the curves, y = ƒ(x) and y = g(x) between the lines, 2x = 1 and 2x = $$\sqrt 3 $$, is :
13
Let a, b $$ \in $$ R, a $$ \ne $$ 0 be such that the equation,
ax2 – 2bx + 5 = 0 has a repeated root $$\alpha $$, which
is also a root of the equation, x2 – 2bx – 10 = 0.
If $$\beta $$ is the other root of this equation, then
$$\alpha $$2 + $$\beta $$2 is equal to :
14
A random variable X has the following
probability distribution :
Then P(X > 2) is equal to :
| X: | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| P(X): | K2 | 2K | K | 2K | 5K2 |
Then P(X > 2) is equal to :
15
If $$x = 2\sin \theta - \sin 2\theta $$ and $$y = 2\cos \theta - \cos 2\theta $$,
$$\theta \in \left[ {0,2\pi } \right]$$, then $${{{d^2}y} \over {d{x^2}}}$$ at $$\theta $$ = $$\pi $$ is :
$$\theta \in \left[ {0,2\pi } \right]$$, then $${{{d^2}y} \over {d{x^2}}}$$ at $$\theta $$ = $$\pi $$ is :
16
Let [t] denote the greatest integer $$ \le $$ t
and $$\mathop {\lim }\limits_{x \to 0} x\left[ {{4 \over x}} \right] = A$$.
Then the function, f(x) = [x2]sin($$\pi $$x) is discontinuous, when x is equal to :
Then the function, f(x) = [x2]sin($$\pi $$x) is discontinuous, when x is equal to :
17
The following system of linear equations
7x + 6y – 2z = 0
3x + 4y + 2z = 0
x – 2y – 6z = 0, has
7x + 6y – 2z = 0
3x + 4y + 2z = 0
x – 2y – 6z = 0, has
18
If the curves, x2 – 6x + y2 + 8 = 0 and
x2 – 8y + y2 + 16 – k = 0, (k > 0) touch each other at a point, then the largest value of k is ______.
x2 – 8y + y2 + 16 – k = 0, (k > 0) touch each other at a point, then the largest value of k is ______.
19
Let $$\overrightarrow a $$, $$\overrightarrow b $$ and $$\overrightarrow c $$ be three vectors such that $$\left| {\overrightarrow a } \right| = \sqrt 3 $$,
$$\left| {\overrightarrow b } \right| = 5,\overrightarrow b .\overrightarrow c = 10$$ and the angle between $$\overrightarrow b $$ and $$\overrightarrow c $$
is $${\pi \over 3}$$. If $${\overrightarrow a }$$ is perpendicular to the vector $$\overrightarrow b \times \overrightarrow c $$ , then $$\left| {\overrightarrow a \times \left( {\overrightarrow b \times \overrightarrow c } \right)} \right|$$ is equal to _____.
20
The number of terms common to the two A.P.'s
3, 7, 11, ....., 407 and 2, 9, 16, ....., 709 is ______.
Physics
1
Starting at temperature 300 K, one mole of an
ideal diatomic gas ($$\gamma $$ = 1.4) is first compressed
adiabatically from volume V1 to V2 = $${{{V_1}} \over {16}}$$. It is
then allowed to expand isobarically to volume 2V2. If all the processes are the quasi-static then
the final temperature of the gas (in oK) is (to the nearest integer) _____.
ideal diatomic gas ($$\gamma $$ = 1.4) is first compressed
adiabatically from volume V1 to V2 = $${{{V_1}} \over {16}}$$. It is
then allowed to expand isobarically to volume 2V2. If all the processes are the quasi-static then
the final temperature of the gas (in oK) is (to the nearest integer) _____.
2
An electric field $$\overrightarrow E = 4x\widehat i - \left( {{y^2} + 1} \right)\widehat j$$ N/C
passes through the box shown in figure. The
flux of the electric field through surfaces ABCD
and BCGF are marked as $${\phi _I}$$ and $${\phi _{II}}$$
respectively. The difference between $$\left( {{\phi _I} - {\phi _{II}}} \right)$$ is (in Nm2/C) _______.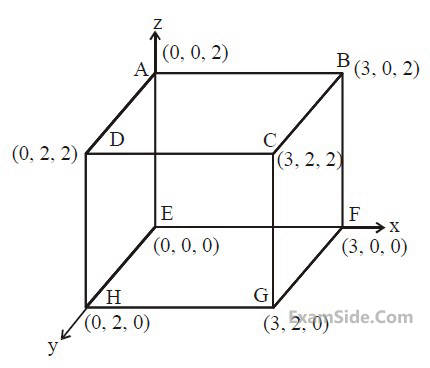
passes through the box shown in figure. The
flux of the electric field through surfaces ABCD
and BCGF are marked as $${\phi _I}$$ and $${\phi _{II}}$$
respectively. The difference between $$\left( {{\phi _I} - {\phi _{II}}} \right)$$ is (in Nm2/C) _______.

3
In a Young's double slit experiment 15 fringes
are observed on a small portion of the screen
when light of wavelength 500 nm is used. Ten
fringes are observed on the same section of
the screen when another light source of
wavelength $$\lambda $$ is used. Then the value of $$\lambda $$ is
(in nm) __________.
4
The circuit shown below is working as a 8 V
dc regulated voltage source. When 12 V is used
as input, the power dissipated (in mW) in each
diode is; (considering both zener diodes are
identical) _________.
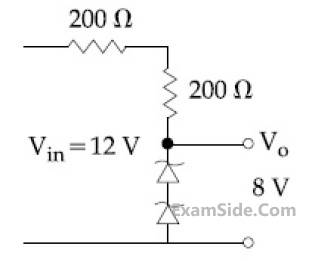

5
In a meter bridge experiment S is a standard
resistance. R is a resistance wire. It is found
that balancing length is $$l$$ = 25 cm. If R is
replaced by a wire of half length and half
diameter that of R of same material, then the
balancing distance $$l'$$ (in cm) will now
be________.
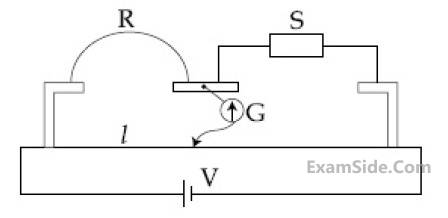

6
Two steel wires having same length are
suspended from a ceiling under the same load.
If the ratio of their energy stored per unit
volume is 1 : 4, the ratio of their diameters is:
7
For the four sets of three measured physical
quantities as given below. Which of the
following options is correct ?
(i) A1 = 24.36, B1 = 0.0724, C1 = 256.2
(ii) A2 = 24.44, B2 = 16.082, C2 = 240.2
(iii) A3 = 25.2, B3 = 19.2812, C3 = 236.183
(iv) A4 = 25, B4 = 236.191, C4 = 19.5
(i) A1 = 24.36, B1 = 0.0724, C1 = 256.2
(ii) A2 = 24.44, B2 = 16.082, C2 = 240.2
(iii) A3 = 25.2, B3 = 19.2812, C3 = 236.183
(iv) A4 = 25, B4 = 236.191, C4 = 19.5
8
Planet A has mass M and radius R. Planet B has
half the mass and half the radius of Planet A.
If the escape velocities from the Planets A and
B are vA and vB, respectively, then $${{{v_A}} \over {{v_B}}} = {n \over 4}$$.
The value of n is :
9
An electron of mass m and magnitude of charge
|e| initially at rest gets accelerated by a constant
electric field E. The rate of change of de-Broglie
wavelength of this electron at time t ignoring
relativistic effects is :
10
A uniformly thick wheel with moment of inertia
I and radius R is free to rotate about its centre
of mass (see fig). A massless string is wrapped
over its rim and two blocks of masses m1 and
m2 (m1 $$ > $$ m2) are attached to the ends of the
string. The system is released from rest. The
angular speed of the wheel when m1 descents
by a distance h is :
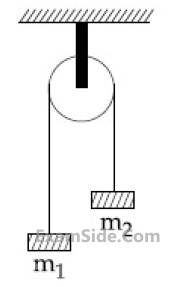

11
Two identical capacitors A and B, charged to
the same potential 5V are connected in two
different circuits as shown below at time t = 0.
If the charge on capacitors A and B at time
t = CR is QA and QB respectively, then (Here
e is the base of natural logarithm)
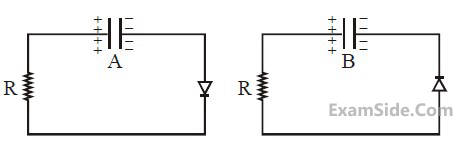

12
The energy required to ionise a hydrogen like
ion in its ground state is 9 Rydbergs. What is
the wavelength of the radiation emitted when
the electron in this ion jumps from the second
excited state to the ground state ?
13
Two gases-argon (atomic radius 0.07 nm,
atomic weight 40) and xenon (atomic radius
0.1 nm, atomic weight 140) have the same
number density and are at the same
temperature. The raito of their respective mean
free times is closest to :
14
An electron gun is placed inside a long solenoid
of radius R on its axis. The solenoid has n
turns/length and carries a current I. The
electron gun shoots an electron along the radius
of the solenoid with speed v. If the electron
does not hit the surface of the solenoid,
maximum possible value of v is (all symbols
have their standard meaning) :
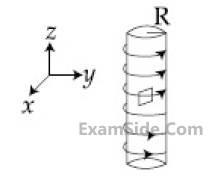

15
A particle of mass m is projected with a speed
u from the ground at an angle
$$\theta = {\pi \over 3}$$ w.r.t.
horizontal (x-axis). When it has reached its
maximum height, it collides completely
inelastically with another particle of the same
mass and velocity $$u\widehat i$$ . The horizontal distance
covered by the combined mass before reaching
the ground is:
16
A particle starts from the origin at t = 0 with an
initial velocity of 3.0 $$\widehat i$$ m/s and moves in the
x-y plane with a constant acceleration $$\left( {6\widehat i + 4\widehat j} \right)$$ m/s2 . The x-coordinate of the particle at the instant when its y-coordinate is 32 m is D meters. The value of D is :-
initial velocity of 3.0 $$\widehat i$$ m/s and moves in the
x-y plane with a constant acceleration $$\left( {6\widehat i + 4\widehat j} \right)$$ m/s2 . The x-coordinate of the particle at the instant when its y-coordinate is 32 m is D meters. The value of D is :-
17
There is a small source of light at some depth
below the surface of water (refractive
index = $${4 \over 3}$$) in a tank of large cross sectional
surface area. Neglecting any reflection from the
bottom and absorption by water, percentage of
light that emerges out of surface is (nearly) :
[Use the fact that surface area of a spherical cap of height h and radius of curvature r is 2$$\pi $$rh]:
[Use the fact that surface area of a spherical cap of height h and radius of curvature r is 2$$\pi $$rh]:
18
A small circular loop of conducting wire has
radius a and carries current I. It is placed in a
uniform magnetic field B perpendicular to its
plane such that when rotated slightly about its
diameter and released, it starts performing
simple harmonic motion of time period T. If the
mass of the loop is m then :
19
The current i in the network is :
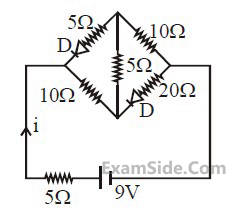

20
A small spherical droplet of density d is floating
exactly half immersed in a liquid of density $$\rho $$
and surface tension T. The radius of the droplet
is (take note that the surface tension applies an
upward force on the droplet) :
21
In LC circuit the inductance L = 40 mH and
capacitance C = 100 $$\mu $$F. If a voltage
V(t) = 10sin(314t) is applied to the circuit, the
current in the circuit is given as :
capacitance C = 100 $$\mu $$F. If a voltage
V(t) = 10sin(314t) is applied to the circuit, the
current in the circuit is given as :
22
A plane electromagnetic wave is propagating
along the direction
$${{\widehat i + \widehat j} \over {\sqrt 2 }}$$
, with its polarization
along the direction $$\widehat k$$ . The correct form of the
magnetic field of the wave would be (here B0
is an appropriate constant) :
23
A rod of length L has non-uniform linear mass
density given by $$\rho $$(x) = $$a + b{\left( {{x \over L}} \right)^2}$$ , where a
and b are constants and 0 $$ \le $$ x $$ \le $$ L. The value
of x for the centre of mass of the rod is at :
density given by $$\rho $$(x) = $$a + b{\left( {{x \over L}} \right)^2}$$ , where a
and b are constants and 0 $$ \le $$ x $$ \le $$ L. The value
of x for the centre of mass of the rod is at :
24
A wire of length L and mass per unit length
6.0 × 10–3 kgm–1 is put under tension of
540 N. Two consecutive frequencies that it
resonates at are : 420 Hz and 490 Hz. Then L
in meters is :
25
A spring mass system (mass m, spring
constant k and natural length $$l$$) rest in
equilibrium on a horizontal disc. The free end
of the spring is fixed at the centre of the disc.
If the disc together with spring mass system,
rotates about it's axis with an angular velocity
$$\omega $$, (k $$ \gg m{\omega ^2}$$) the relative change in the length
of the spring is best given by the option :