Chemistry
1
The increasing order of the atomic radii of the
following elements is :-
(a) C (b) O
(c) F (d) Cl
(e) Br
(a) C (b) O
(c) F (d) Cl
(e) Br
2
Consider the following plots of rate constant
versus $${1 \over T}$$ for four different reactions. Which
of the following orders is correct for the
activation energies of these reactions?


3
Kjeldahl's method cannot be used to estimate
nitrogen for which of the following
compounds?
4
Among the compounds A and B with
molecular formula C9H18O3 , A is having higher
boiling point the B. The possible structures of
A and B are :
5
An unsaturated hydrocarbon X absorbs two
hydrogen molecules on catalytic hydrogenation and also gives following reaction :
 B(3 - oxo - hexanedicarboxylic acid) X will be :-
B(3 - oxo - hexanedicarboxylic acid) X will be :-
 B(3 - oxo - hexanedicarboxylic acid) X will be :-
B(3 - oxo - hexanedicarboxylic acid) X will be :-6
For the following Assertion and Reason, the
correct option is :
Assertion : The pH of water increases with increase in temperature.
Reason : The dissociation of water into H+ and OH– is an exothermic reaction.
Assertion : The pH of water increases with increase in temperature.
Reason : The dissociation of water into H+ and OH– is an exothermic reaction.
7
The radius of the second Bohr orbit, in terms
of the Bohr radius, a0, in Li2+ is :
8
Complexes (ML5) of metals Ni and Fe have
ideal square pyramidal and trigonal
bipyramidal grometries, respectively. The sum
of the 90°, 120° and 180° L-M-L angles in the
two complexes is ________.
9
At constant volume, 4 mol of an ideal gas when
heated from 300 K to 500K changes its internal
energy by 5000 J. The molar heat capacity at
constant volume is _______.
10
In the following sequence of reactions the
maximum number of atoms present in
molecule 'C' in one plane is _________.
 (A is a lowest molecular weight alkyne)
(A is a lowest molecular weight alkyne)
 (A is a lowest molecular weight alkyne)
(A is a lowest molecular weight alkyne)11
For an electrochemical cell
Sn(s) | Sn2+ (aq,1M)||Pb2+ (aq,1M)|Pb(s)
the ratio $${{\left[ {S{n^{2 + }}} \right]} \over {\left[ {P{b^{2 + }}} \right]}}$$ when this cell attains equilibrium is _________.
(Given $$E_{S{n^{2 + }}|Sn}^0 = - 0.14V$$,
$$E_{P{b^{2 + }}|Pb}^0 = - 0.13V$$, $${{2.303RT} \over F} = 0.06$$)
Sn(s) | Sn2+ (aq,1M)||Pb2+ (aq,1M)|Pb(s)
the ratio $${{\left[ {S{n^{2 + }}} \right]} \over {\left[ {P{b^{2 + }}} \right]}}$$ when this cell attains equilibrium is _________.
(Given $$E_{S{n^{2 + }}|Sn}^0 = - 0.14V$$,
$$E_{P{b^{2 + }}|Pb}^0 = - 0.13V$$, $${{2.303RT} \over F} = 0.06$$)
12
The correct order of the calculated spin-only
magnetic moments of complexs (A) to (D) is:
(A) Ni(CO)4
(B) [Ni(H2O)6]Cl2
(C) Na2[Ni(CN)4]
(D) PdCl2(PPh3)2
(A) Ni(CO)4
(B) [Ni(H2O)6]Cl2
(C) Na2[Ni(CN)4]
(D) PdCl2(PPh3)2
13
Hydrogen has three isotopes (A), (B) and (C).
If the number of neutron(s) in (A), (B) and (C)
respectively, are (x), (y) and (z), the sum of (x),
(y) an (z) is :
14
The major product in the following reaction is:


15
Among (a) – (d) the complexes that can display
geometrical isomerism are :
(a) [Pt(NH3)3Cl]+
(b) [Pt(NH3)Cl5]–
(c) [Pt(NH3)2Cl(NO2)]
(d) [Pt(NH3)4ClBr]2+
(a) [Pt(NH3)3Cl]+
(b) [Pt(NH3)Cl5]–
(c) [Pt(NH3)2Cl(NO2)]
(d) [Pt(NH3)4ClBr]2+
16
Two monomers in maltose are :
17
Arrange the following bonds according to their
average bond energies in descending order :
C–Cl, C–Br, C–F, C–I
C–Cl, C–Br, C–F, C–I
18
A metal (A) on heating in nitrogen gas gives
compound B. B on treatment with H2O gives
a colourless gas which when passed through
CuSO4 solution gives a dark blue-violet
coloured solution. A and B respectively, are :
19
The major product [B] in the following
sequence of reactions is :-


Mathematics
1
Let ƒ(x) be a polynomial of degree 3 such that
ƒ(–1) = 10, ƒ(1) = –6, ƒ(x) has a critical point
at x = –1 and ƒ'(x) has a critical point at x = 1.
Then ƒ(x) has a local minima at x = _______.
2
The number of 4 letter words (with or without
meaning) that can be formed from the eleven
letters of the word 'EXAMINATION' is
_______.
3
$$\mathop {\lim }\limits_{x \to 0} {{\int_0^x {t\sin \left( {10t} \right)dt} } \over x}$$ is equal to
4
If $$A = \left( {\matrix{
2 & 2 \cr
9 & 4 \cr
} } \right)$$ and $$I = \left( {\matrix{
1 & 0 \cr
0 & 1 \cr
} } \right)$$ then 10A–1 is
equal to :
5
The mean and variance of 20 observations are
found to be 10 and 4, respectively. On
rechecking, it was found that an observation 9
was incorrect and the correct observation was
11. Then the correct variance is
6
If $${{\sqrt 2 \sin \alpha } \over {\sqrt {1 + \cos 2\alpha } }} = {1 \over 7}$$ and $$\sqrt {{{1 - \cos 2\beta } \over 2}} = {1 \over {\sqrt {10} }}$$
$$\alpha ,\beta \in \left( {0,{\pi \over 2}} \right)$$ then tan($$\alpha $$ + 2$$\beta $$) is equal to _____.
$$\alpha ,\beta \in \left( {0,{\pi \over 2}} \right)$$ then tan($$\alpha $$ + 2$$\beta $$) is equal to _____.
7
Let $$\alpha = {{ - 1 + i\sqrt 3 } \over 2}$$.
If $$a = \left( {1 + \alpha } \right)\sum\limits_{k = 0}^{100} {{\alpha ^{2k}}} $$ and
$$b = \sum\limits_{k = 0}^{100} {{\alpha ^{3k}}} $$, then a and b are the roots of the quadratic equation :
If $$a = \left( {1 + \alpha } \right)\sum\limits_{k = 0}^{100} {{\alpha ^{2k}}} $$ and
$$b = \sum\limits_{k = 0}^{100} {{\alpha ^{3k}}} $$, then a and b are the roots of the quadratic equation :
8
Let A and B be two events such that the
probability that exactly one of them occurs is $${2 \over 5}$$ and the probability that A or B occurs is $${1 \over 2}$$ ,
then the probability of both of them occur
together is :
9
If $$I = \int\limits_1^2 {{{dx} \over {\sqrt {2{x^3} - 9{x^2} + 12x + 4} }}} $$, then :
10
Let S be the set of all real roots of the equation,
3x(3x – 1) + 2 = |3x – 1| + |3x – 2|. Then S :
3x(3x – 1) + 2 = |3x – 1| + |3x – 2|. Then S :
11
If $$\alpha $$ and $$\beta $$ be the coefficients of x4 and x2
respectively in the expansion of
$${\left( {x + \sqrt {{x^2} - 1} } \right)^6} + {\left( {x - \sqrt {{x^2} - 1} } \right)^6}$$, then
$${\left( {x + \sqrt {{x^2} - 1} } \right)^6} + {\left( {x - \sqrt {{x^2} - 1} } \right)^6}$$, then
12
The system of linear equations
$$\lambda $$x + 2y + 2z = 5
2$$\lambda $$x + 3y + 5z = 8
4x + $$\lambda $$y + 6z = 10 has
$$\lambda $$x + 2y + 2z = 5
2$$\lambda $$x + 3y + 5z = 8
4x + $$\lambda $$y + 6z = 10 has
13
Let ƒ : (1, 3) $$ \to $$ R be a function defined by
$$f(x) = {{x\left[ x \right]} \over {1 + {x^2}}}$$ , where [x] denotes the greatest integer $$ \le $$ x. Then the range of ƒ is
$$f(x) = {{x\left[ x \right]} \over {1 + {x^2}}}$$ , where [x] denotes the greatest integer $$ \le $$ x. Then the range of ƒ is
14
If the 10th term of an A.P. is $${1 \over {20}}$$ and its 20th term
is $${1 \over {10}}$$, then the sum of its first 200 terms is
15
Let S be the set of all functions ƒ : [0,1] $$ \to $$ R,
which are continuous on [0,1] and differentiable
on (0,1). Then for every ƒ in S, there exists a
c $$ \in $$ (0,1), depending on ƒ, such that
16
The area (in sq. units) of the region
{(x,y) $$ \in $$ R2 : x2 $$ \le $$ y $$ \le $$ 3 – 2x}, is :
{(x,y) $$ \in $$ R2 : x2 $$ \le $$ y $$ \le $$ 3 – 2x}, is :
17
Let $$\overrightarrow a = \widehat i - 2\widehat j + \widehat k$$ and $$\overrightarrow b = \widehat i - \widehat j + \widehat k$$ be two
vectors. If $$\overrightarrow c $$ is a vector such that $$\overrightarrow b \times \overrightarrow c = \overrightarrow b \times \overrightarrow a $$ and $$\overrightarrow c .\overrightarrow a = 0$$, then $$\overrightarrow c .\overrightarrow b $$ is equal to
Physics
1
A capacitor is made of two square plates each
of side 'a' making a very small angle $$\alpha $$ between
them, as shown in figure. The capacitance will
be close to :


2
An object is gradually moving away from the
focal point of a concave mirror along the axis
of the mirror. The graphical representation of
the magnitude of linear magnification (m)
versus distance of the object from the mirror
(x) is correctly given by :
(Graphs are drawn schematically and are not to scale)
(Graphs are drawn schematically and are not to scale)
3
A particle moves such that its position
vector $$\overrightarrow r \left( t \right) = \cos \omega t\widehat i + \sin \omega t\widehat j$$ where $$\omega $$ is a constant and t is time. Then which of the following statements is true for the velocity
$$\overrightarrow v \left( t \right)$$ and acceleration $$\overrightarrow a \left( t \right)$$ of the particle :
4
Consider two charged metallic spheres S1 and
S2 of radii R1 and R2, respectively. The electric
fields E1 (on S1) and E2 (on S2) on their surfaces
are such that E1/E2 = R1/R2. Then the ratio
V1 (on S1) / V2 (on S2) of the electrostatic
potentials on each sphere is :
5
An electron (mass m) with initial velocity $$\overrightarrow v = {v_0}\widehat i + {v_0}\widehat j$$ is in an electric field $$\overrightarrow E = - {E_0}\widehat k$$. If $$\lambda _0$$ is initial de-Broglie wavelength of electron,
its de-Broglie wave length at time t is given
by :
6
A uniform sphere of mass 500 g rolls without
slipping on a plane horizontal surface with its
centre moving at a speed of 5.00 cm/s. Its
kinetic energy is :
7
Consider a mixture of n moles of helium gas
and 2n moles of oxygen gas (molecules taken
to be rigid) as an ideal gas. Its CP/CV value
will be :
8
A particle of mass m is dropped from a height
h above the ground. At the same time another
particle of the same mass is thrown vertically
upwards from the ground with a speed of $$\sqrt {2gh} $$. If they collide head-on completely
inelastically, the time taken for the combined
mass to reach the ground, in units of $$\sqrt {{h \over g}} $$ is :
9
A very long wire ABDMNDC is shown in
figure carrying current I. AB and BC parts are
straight, long and at right angle. At D wire
forms a circular turn DMND of radius R. AB,
BC parts are tangential to circular turn at N and
D. Magnetic field at the centre of circle is :
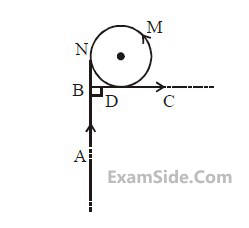

10
In the given circuit, value of Y is :


11
A shown in the figure, a battery of emf $$\varepsilon $$ is
connected to an inductor L and resistance R in
series. The switch is closed at t = 0. The total
charge that flows from the battery, between
t = 0 and t = tc (tc is the time constant of the
circuit) is :
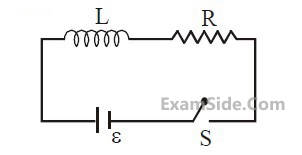

12
A transverse wave travels on a taut steel wire
with a velocity of v when tension in it is
2.06 × 104 N. When the tension is changed to
T, the velocity changed to v/2. The value of T
is close to :
13
Two liquids of densities $${\rho _1}$$ an $${\rho _2}$$ ($${\rho _2}$$ = 2$${\rho _1}$$) are
filled up behind a square wall of side 10 m as
shown in figure. Each liquid has a height of
5 m. The ratio of the forces due to these liquids
exerted on upper part MN to that at the lower part
NO is (Assume that the liquids are not mixing)


14
A particle of mass m and charge q is released
from rest in a uniform electric field. If there is
no other force on the particle, the dependence
of its speed v on the distance x travelled by it
is correctly given by (graphs are schematic and
not drawn to scale)
15
A simple pendulum is being used to determine
th value of gravitational acceleration g at a
certain place. Th length of the pendulum is
25.0 cm and a stop watch with 1s resolution
measures the time taken for 40 oscillations to
be 50 s. The accuracy in g is :
16
A galvanometer having a coil resistance
100 $$\Omega $$ gives a full scale deflection when a
current of 1 mA is passed through it. What is
the value of the resistance which can convert
this galvanometer into a voltmeter giving full
scale deflection for a potential difference of
10 V?
17
A plane electromagnetic wave of frequency
25 GHz is propagating in vacuum along the
z-direction. At a particular point in space and
time, the magnetic field is given by $$\overrightarrow B = 5 \times {10^{ - 8}}\widehat jT$$. The corresponding electric field $$\overrightarrow E $$ is (speed of light c = 3 × 108 ms–1)
18
In a double slit experiment, at a certain point
on the screen the path difference between the
two interfering waves is $${1 \over 8}$$th of a wavelength.
The ratio of the intensity of light at that point
to that at the centre of a bright fringe is :
19
As shown in figure, when a spherical cavity
(centered at O) of radius 1 is cut out of a uniform
sphere of radius R (centered at C), the centre of
mass of remaining (shaded) part of sphere is at
G, i.e, on the surface of the cavity. R can be
detemined by the equation :


20
The series combination of two batteries, both
of the same emf 10 V, but different internal
resistance of 20$$\Omega $$ and 5$$\Omega $$, is connected to the
parallel combination of two resistors 30$$\Omega $$ and
R $$\Omega $$. The voltage difference across the battery
of internal resistance 20$$\Omega $$ is zero, the value of
R (in $$\Omega $$) is : _______
21
An asteroid is moving directly towards the
centre of the earth. When at a distance of
10R (R is the radius of the earth) from the earths
centre, it has a speed of 12 km/s. Neglecting
the effect of earths atmosphere, what will be the
speed of the asteroid when it hits the surface
of the earth (escape velocity from the earth is
11.2 km/s) ? Give your answer to the nearest
integer in kilometer/s _____.
22
The first member of the Balmer series of
hydrogen atom has a wavelength of 6561 Å.
The wavelength of the second member of the
Balmer series (in nm) is:
23
A ball is dropped from the top of a 100 m high
tower on a planet. In the last $${1 \over 2}s$$ before hitting
the ground, it covers a distance of 19 m.
Acceleration due to gravity (in ms–2) near the
surface on that planet is _____.
24
Three containers C1, C2 and C3 have water at
different temperatures. The table below shows
the final temperature T when different amounts
of water (given in litres) are taken from each
containers and mixed (assume no loss of heat
during the process)
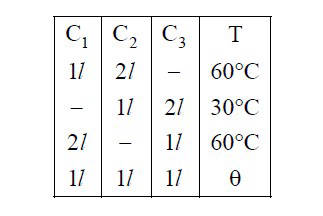 The value of $$\theta $$ (in °C to the nearest integer) is ..........
The value of $$\theta $$ (in °C to the nearest integer) is ..........
 The value of $$\theta $$ (in °C to the nearest integer) is ..........
The value of $$\theta $$ (in °C to the nearest integer) is ..........1
JEE Main 2020 (Online) 8th January Evening Slot
MCQ (Single Correct Answer)
+4
-1
The system of linear equations
$$\lambda $$x + 2y + 2z = 5
2$$\lambda $$x + 3y + 5z = 8
4x + $$\lambda $$y + 6z = 10 has
$$\lambda $$x + 2y + 2z = 5
2$$\lambda $$x + 3y + 5z = 8
4x + $$\lambda $$y + 6z = 10 has
2
JEE Main 2020 (Online) 8th January Evening Slot
MCQ (Single Correct Answer)
+4
-1
Let ƒ : (1, 3) $$ \to $$ R be a function defined by
$$f(x) = {{x\left[ x \right]} \over {1 + {x^2}}}$$ , where [x] denotes the greatest integer $$ \le $$ x. Then the range of ƒ is
$$f(x) = {{x\left[ x \right]} \over {1 + {x^2}}}$$ , where [x] denotes the greatest integer $$ \le $$ x. Then the range of ƒ is
3
JEE Main 2020 (Online) 8th January Evening Slot
MCQ (Single Correct Answer)
+4
-1
If the 10th term of an A.P. is $${1 \over {20}}$$ and its 20th term
is $${1 \over {10}}$$, then the sum of its first 200 terms is
4
JEE Main 2020 (Online) 8th January Evening Slot
MCQ (Single Correct Answer)
+4
-1
Let S be the set of all functions ƒ : [0,1] $$ \to $$ R,
which are continuous on [0,1] and differentiable
on (0,1). Then for every ƒ in S, there exists a
c $$ \in $$ (0,1), depending on ƒ, such that
Subject
Chemistry
19
Mathematics
17
Physics
24
More Papers of JEE Main
2025
JEE Main 2025 (Online) 8th April Evening ShiftJEE Main 2025 (Online) 7th April Evening ShiftJEE Main 2025 (Online) 7th April Morning ShiftJEE Main 2025 (Online) 4th April Evening ShiftJEE Main 2025 (Online) 4th April Morning ShiftJEE Main 2025 (Online) 3rd April Evening ShiftJEE Main 2025 (Online) 3rd April Morning ShiftJEE Main 2025 (Online) 2nd April Evening ShiftJEE Main 2025 (Online) 2nd April Morning ShiftJEE Main 2025 (Online) 29th January Evening ShiftJEE Main 2025 (Online) 29th January Morning ShiftJEE Main 2025 (Online) 28th January Evening ShiftJEE Main 2025 (Online) 28th January Morning ShiftJEE Main 2025 (Online) 24th January Evening ShiftJEE Main 2025 (Online) 24th January Morning ShiftJEE Main 2025 (Online) 23rd January Evening ShiftJEE Main 2025 (Online) 23rd January Morning ShiftJEE Main 2025 (Online) 22nd January Evening ShiftJEE Main 2025 (Online) 22nd January Morning Shift2024
JEE Main 2024 (Online) 9th April Evening ShiftJEE Main 2024 (Online) 9th April Morning ShiftJEE Main 2024 (Online) 8th April Evening ShiftJEE Main 2024 (Online) 8th April Morning ShiftJEE Main 2024 (Online) 6th April Evening ShiftJEE Main 2024 (Online) 6th April Morning ShiftJEE Main 2024 (Online) 5th April Evening ShiftJEE Main 2024 (Online) 5th April Morning ShiftJEE Main 2024 (Online) 4th April Evening ShiftJEE Main 2024 (Online) 4th April Morning ShiftJEE Main 2024 (Online) 1st February Evening ShiftJEE Main 2024 (Online) 1st February Morning ShiftJEE Main 2024 (Online) 31st January Evening ShiftJEE Main 2024 (Online) 31st January Morning ShiftJEE Main 2024 (Online) 30th January Evening ShiftJEE Main 2024 (Online) 30th January Morning ShiftJEE Main 2024 (Online) 29th January Evening ShiftJEE Main 2024 (Online) 29th January Morning ShiftJEE Main 2024 (Online) 27th January Evening ShiftJEE Main 2024 (Online) 27th January Morning Shift2023
JEE Main 2023 (Online) 15th April Morning ShiftJEE Main 2023 (Online) 13th April Evening ShiftJEE Main 2023 (Online) 13th April Morning ShiftJEE Main 2023 (Online) 12th April Morning ShiftJEE Main 2023 (Online) 11th April Evening ShiftJEE Main 2023 (Online) 11th April Morning ShiftJEE Main 2023 (Online) 10th April Evening ShiftJEE Main 2023 (Online) 10th April Morning ShiftJEE Main 2023 (Online) 8th April Evening ShiftJEE Main 2023 (Online) 8th April Morning ShiftJEE Main 2023 (Online) 6th April Evening ShiftJEE Main 2023 (Online) 6th April Morning ShiftJEE Main 2023 (Online) 1st February Evening ShiftJEE Main 2023 (Online) 1st February Morning ShiftJEE Main 2023 (Online) 31st January Evening ShiftJEE Main 2023 (Online) 31st January Morning ShiftJEE Main 2023 (Online) 30th January Evening ShiftJEE Main 2023 (Online) 30th January Morning ShiftJEE Main 2023 (Online) 29th January Evening ShiftJEE Main 2023 (Online) 29th January Morning ShiftJEE Main 2023 (Online) 25th January Evening ShiftJEE Main 2023 (Online) 25th January Morning ShiftJEE Main 2023 (Online) 24th January Evening ShiftJEE Main 2023 (Online) 24th January Morning Shift2022
JEE Main 2022 (Online) 29th July Evening ShiftJEE Main 2022 (Online) 29th July Morning ShiftJEE Main 2022 (Online) 28th July Evening ShiftJEE Main 2022 (Online) 28th July Morning ShiftJEE Main 2022 (Online) 27th July Evening ShiftJEE Main 2022 (Online) 27th July Morning ShiftJEE Main 2022 (Online) 26th July Evening ShiftJEE Main 2022 (Online) 26th July Morning ShiftJEE Main 2022 (Online) 25th July Evening ShiftJEE Main 2022 (Online) 25th July Morning ShiftJEE Main 2022 (Online) 30th June Morning ShiftJEE Main 2022 (Online) 29th June Evening ShiftJEE Main 2022 (Online) 29th June Morning ShiftJEE Main 2022 (Online) 28th June Evening ShiftJEE Main 2022 (Online) 28th June Morning ShiftJEE Main 2022 (Online) 27th June Evening ShiftJEE Main 2022 (Online) 27th June Morning ShiftJEE Main 2022 (Online) 26th June Evening ShiftJEE Main 2022 (Online) 26th June Morning ShiftJEE Main 2022 (Online) 25th June Evening ShiftJEE Main 2022 (Online) 25th June Morning ShiftJEE Main 2022 (Online) 24th June Evening ShiftJEE Main 2022 (Online) 24th June Morning Shift2021
JEE Main 2021 (Online) 1st September Evening ShiftJEE Main 2021 (Online) 31st August Evening ShiftJEE Main 2021 (Online) 31st August Morning ShiftJEE Main 2021 (Online) 27th August Evening ShiftJEE Main 2021 (Online) 27th August Morning ShiftJEE Main 2021 (Online) 26th August Evening ShiftJEE Main 2021 (Online) 26th August Morning ShiftJEE Main 2021 (Online) 27th July Evening ShiftJEE Main 2021 (Online) 27th July Morning ShiftJEE Main 2021 (Online) 25th July Evening ShiftJEE Main 2021 (Online) 25th July Morning ShiftJEE Main 2021 (Online) 22th July Evening ShiftJEE Main 2021 (Online) 20th July Evening ShiftJEE Main 2021 (Online) 20th July Morning ShiftJEE Main 2021 (Online) 18th March Evening ShiftJEE Main 2021 (Online) 18th March Morning ShiftJEE Main 2021 (Online) 17th March Evening ShiftJEE Main 2021 (Online) 17th March Morning ShiftJEE Main 2021 (Online) 16th March Evening ShiftJEE Main 2021 (Online) 16th March Morning ShiftJEE Main 2021 (Online) 26th February Evening ShiftJEE Main 2021 (Online) 26th February Morning ShiftJEE Main 2021 (Online) 25th February Evening ShiftJEE Main 2021 (Online) 25th February Morning ShiftJEE Main 2021 (Online) 24th February Evening ShiftJEE Main 2021 (Online) 24th February Morning Shift2020
JEE Main 2020 (Online) 6th September Evening SlotJEE Main 2020 (Online) 6th September Morning SlotJEE Main 2020 (Online) 5th September Evening SlotJEE Main 2020 (Online) 5th September Morning SlotJEE Main 2020 (Online) 4th September Evening SlotJEE Main 2020 (Online) 4th September Morning SlotJEE Main 2020 (Online) 3rd September Evening SlotJEE Main 2020 (Online) 3rd September Morning SlotJEE Main 2020 (Online) 2nd September Evening SlotJEE Main 2020 (Online) 2nd September Morning SlotJEE Main 2020 (Online) 9th January Evening SlotJEE Main 2020 (Online) 9th January Morning SlotJEE Main 2020 (Online) 8th January Evening SlotJEE Main 2020 (Online) 8th January Morning SlotJEE Main 2020 (Online) 7th January Evening SlotJEE Main 2020 (Online) 7th January Morning Slot2019
JEE Main 2019 (Online) 12th April Evening SlotJEE Main 2019 (Online) 12th April Morning SlotJEE Main 2019 (Online) 10th April Evening SlotJEE Main 2019 (Online) 10th April Morning SlotJEE Main 2019 (Online) 9th April Evening SlotJEE Main 2019 (Online) 9th April Morning SlotJEE Main 2019 (Online) 8th April Evening SlotJEE Main 2019 (Online) 8th April Morning SlotJEE Main 2019 (Online) 12th January Evening SlotJEE Main 2019 (Online) 12th January Morning SlotJEE Main 2019 (Online) 11th January Evening SlotJEE Main 2019 (Online) 11th January Morning SlotJEE Main 2019 (Online) 10th January Evening SlotJEE Main 2019 (Online) 10th January Morning SlotJEE Main 2019 (Online) 9th January Evening SlotJEE Main 2019 (Online) 9th January Morning Slot2018
JEE Main 2018 (Online) 16th April Morning SlotJEE Main 2018 (Offline)JEE Main 2018 (Online) 15th April Evening SlotJEE Main 2018 (Online) 15th April Morning Slot2017
JEE Main 2017 (Online) 9th April Morning SlotJEE Main 2017 (Online) 8th April Morning SlotJEE Main 2017 (Offline)2016
JEE Main 2016 (Online) 10th April Morning SlotJEE Main 2016 (Online) 9th April Morning SlotJEE Main 2016 (Offline)2015
JEE Main 2015 (Offline)2014
JEE Main 2014 (Offline)2013
JEE Main 2013 (Offline)2012
AIEEE 20122011
AIEEE 20112010
AIEEE 20102009
AIEEE 20092008
AIEEE 20082007
AIEEE 20072006
AIEEE 20062005
AIEEE 20052004
AIEEE 20042003
AIEEE 20032002
AIEEE 2002