2025
JEE Main 2025 (Online) 8th April Evening ShiftJEE Main 2025 (Online) 7th April Evening ShiftJEE Main 2025 (Online) 7th April Morning ShiftJEE Main 2025 (Online) 4th April Evening ShiftJEE Main 2025 (Online) 4th April Morning ShiftJEE Main 2025 (Online) 3rd April Evening ShiftJEE Main 2025 (Online) 3rd April Morning ShiftJEE Main 2025 (Online) 2nd April Evening ShiftJEE Main 2025 (Online) 2nd April Morning ShiftJEE Main 2025 (Online) 29th January Evening ShiftJEE Main 2025 (Online) 29th January Morning ShiftJEE Main 2025 (Online) 28th January Evening ShiftJEE Main 2025 (Online) 28th January Morning ShiftJEE Main 2025 (Online) 24th January Evening ShiftJEE Main 2025 (Online) 24th January Morning ShiftJEE Main 2025 (Online) 23rd January Evening ShiftJEE Main 2025 (Online) 23rd January Morning ShiftJEE Main 2025 (Online) 22nd January Evening ShiftJEE Main 2025 (Online) 22nd January Morning Shift2024
JEE Main 2024 (Online) 9th April Evening ShiftJEE Main 2024 (Online) 9th April Morning ShiftJEE Main 2024 (Online) 8th April Evening ShiftJEE Main 2024 (Online) 8th April Morning ShiftJEE Main 2024 (Online) 6th April Evening ShiftJEE Main 2024 (Online) 6th April Morning ShiftJEE Main 2024 (Online) 5th April Evening ShiftJEE Main 2024 (Online) 5th April Morning ShiftJEE Main 2024 (Online) 4th April Evening ShiftJEE Main 2024 (Online) 4th April Morning ShiftJEE Main 2024 (Online) 1st February Evening ShiftJEE Main 2024 (Online) 1st February Morning ShiftJEE Main 2024 (Online) 31st January Evening ShiftJEE Main 2024 (Online) 31st January Morning ShiftJEE Main 2024 (Online) 30th January Evening ShiftJEE Main 2024 (Online) 30th January Morning ShiftJEE Main 2024 (Online) 29th January Evening ShiftJEE Main 2024 (Online) 29th January Morning ShiftJEE Main 2024 (Online) 27th January Evening ShiftJEE Main 2024 (Online) 27th January Morning Shift2023
JEE Main 2023 (Online) 15th April Morning ShiftJEE Main 2023 (Online) 13th April Evening ShiftJEE Main 2023 (Online) 13th April Morning ShiftJEE Main 2023 (Online) 12th April Morning ShiftJEE Main 2023 (Online) 11th April Evening ShiftJEE Main 2023 (Online) 11th April Morning ShiftJEE Main 2023 (Online) 10th April Evening ShiftJEE Main 2023 (Online) 10th April Morning ShiftJEE Main 2023 (Online) 8th April Evening ShiftJEE Main 2023 (Online) 8th April Morning ShiftJEE Main 2023 (Online) 6th April Evening ShiftJEE Main 2023 (Online) 6th April Morning ShiftJEE Main 2023 (Online) 1st February Evening ShiftJEE Main 2023 (Online) 1st February Morning ShiftJEE Main 2023 (Online) 31st January Evening ShiftJEE Main 2023 (Online) 31st January Morning ShiftJEE Main 2023 (Online) 30th January Evening ShiftJEE Main 2023 (Online) 30th January Morning ShiftJEE Main 2023 (Online) 29th January Evening ShiftJEE Main 2023 (Online) 29th January Morning ShiftJEE Main 2023 (Online) 25th January Evening ShiftJEE Main 2023 (Online) 25th January Morning ShiftJEE Main 2023 (Online) 24th January Evening ShiftJEE Main 2023 (Online) 24th January Morning Shift2022
JEE Main 2022 (Online) 29th July Evening ShiftJEE Main 2022 (Online) 29th July Morning ShiftJEE Main 2022 (Online) 28th July Evening ShiftJEE Main 2022 (Online) 28th July Morning ShiftJEE Main 2022 (Online) 27th July Evening ShiftJEE Main 2022 (Online) 27th July Morning ShiftJEE Main 2022 (Online) 26th July Evening ShiftJEE Main 2022 (Online) 26th July Morning ShiftJEE Main 2022 (Online) 25th July Evening ShiftJEE Main 2022 (Online) 25th July Morning ShiftJEE Main 2022 (Online) 30th June Morning ShiftJEE Main 2022 (Online) 29th June Evening ShiftJEE Main 2022 (Online) 29th June Morning ShiftJEE Main 2022 (Online) 28th June Evening ShiftJEE Main 2022 (Online) 28th June Morning ShiftJEE Main 2022 (Online) 27th June Evening ShiftJEE Main 2022 (Online) 27th June Morning ShiftJEE Main 2022 (Online) 26th June Evening ShiftJEE Main 2022 (Online) 26th June Morning ShiftJEE Main 2022 (Online) 25th June Evening ShiftJEE Main 2022 (Online) 25th June Morning ShiftJEE Main 2022 (Online) 24th June Evening ShiftJEE Main 2022 (Online) 24th June Morning Shift2021
JEE Main 2021 (Online) 1st September Evening ShiftJEE Main 2021 (Online) 31st August Evening ShiftJEE Main 2021 (Online) 31st August Morning ShiftJEE Main 2021 (Online) 27th August Evening ShiftJEE Main 2021 (Online) 27th August Morning ShiftJEE Main 2021 (Online) 26th August Evening ShiftJEE Main 2021 (Online) 26th August Morning ShiftJEE Main 2021 (Online) 27th July Evening ShiftJEE Main 2021 (Online) 27th July Morning ShiftJEE Main 2021 (Online) 25th July Evening ShiftJEE Main 2021 (Online) 25th July Morning ShiftJEE Main 2021 (Online) 22th July Evening ShiftJEE Main 2021 (Online) 20th July Evening ShiftJEE Main 2021 (Online) 20th July Morning ShiftJEE Main 2021 (Online) 18th March Evening ShiftJEE Main 2021 (Online) 18th March Morning ShiftJEE Main 2021 (Online) 17th March Evening ShiftJEE Main 2021 (Online) 17th March Morning ShiftJEE Main 2021 (Online) 16th March Evening ShiftJEE Main 2021 (Online) 16th March Morning ShiftJEE Main 2021 (Online) 26th February Evening ShiftJEE Main 2021 (Online) 26th February Morning ShiftJEE Main 2021 (Online) 25th February Evening ShiftJEE Main 2021 (Online) 25th February Morning ShiftJEE Main 2021 (Online) 24th February Evening ShiftJEE Main 2021 (Online) 24th February Morning Shift2020
JEE Main 2020 (Online) 6th September Evening SlotJEE Main 2020 (Online) 6th September Morning SlotJEE Main 2020 (Online) 5th September Evening SlotJEE Main 2020 (Online) 5th September Morning SlotJEE Main 2020 (Online) 4th September Evening SlotJEE Main 2020 (Online) 4th September Morning SlotJEE Main 2020 (Online) 3rd September Evening SlotJEE Main 2020 (Online) 3rd September Morning SlotJEE Main 2020 (Online) 2nd September Evening SlotJEE Main 2020 (Online) 2nd September Morning SlotJEE Main 2020 (Online) 9th January Evening SlotJEE Main 2020 (Online) 9th January Morning SlotJEE Main 2020 (Online) 8th January Evening SlotJEE Main 2020 (Online) 8th January Morning SlotJEE Main 2020 (Online) 7th January Evening SlotJEE Main 2020 (Online) 7th January Morning Slot2019
JEE Main 2019 (Online) 12th April Evening SlotJEE Main 2019 (Online) 12th April Morning SlotJEE Main 2019 (Online) 10th April Evening SlotJEE Main 2019 (Online) 10th April Morning SlotJEE Main 2019 (Online) 9th April Evening SlotJEE Main 2019 (Online) 9th April Morning SlotJEE Main 2019 (Online) 8th April Evening SlotJEE Main 2019 (Online) 8th April Morning SlotJEE Main 2019 (Online) 12th January Evening SlotJEE Main 2019 (Online) 12th January Morning SlotJEE Main 2019 (Online) 11th January Evening SlotJEE Main 2019 (Online) 11th January Morning SlotJEE Main 2019 (Online) 10th January Evening SlotJEE Main 2019 (Online) 10th January Morning SlotJEE Main 2019 (Online) 9th January Evening SlotJEE Main 2019 (Online) 9th January Morning Slot2018
JEE Main 2018 (Online) 16th April Morning SlotJEE Main 2018 (Offline)JEE Main 2018 (Online) 15th April Evening SlotJEE Main 2018 (Online) 15th April Morning Slot2017
JEE Main 2017 (Online) 9th April Morning SlotJEE Main 2017 (Online) 8th April Morning SlotJEE Main 2017 (Offline)2016
JEE Main 2016 (Online) 10th April Morning SlotJEE Main 2016 (Online) 9th April Morning SlotJEE Main 2016 (Offline)2015
JEE Main 2015 (Offline)2014
JEE Main 2014 (Offline)2013
JEE Main 2013 (Offline)2012
AIEEE 20122011
AIEEE 20112010
AIEEE 20102009
AIEEE 20092008
AIEEE 20082007
AIEEE 20072006
AIEEE 20062005
AIEEE 20052004
AIEEE 20042003
AIEEE 20032002
AIEEE 2002JEE Main 2019 (Online) 8th April Evening Slot
Paper was held on Mon, Apr 8, 2019 9:30 AM
Chemistry
1
For the solution of the gases w, x, y and z in
water at 298K, the Henrys law constants (KH)
are 0.5, 2, 35 and 40 kbar, respectively. The
correct plot for the given data is :-
2
Polysubstitution is a major drawback in:
3
If p is the momentum of the fastest electron
ejected from a metal surface after the irradiation
of light having wavelength $$\lambda $$, then for 1.5 p
momentum of the photoelectron, the
wavelength of the light should be:
(Assume kinetic energy of ejected
photoelectron to be very high in comparison
to work function)
4
Fructose and glucose can be distinguished by :
5
The major product obtained in the following
reaction is
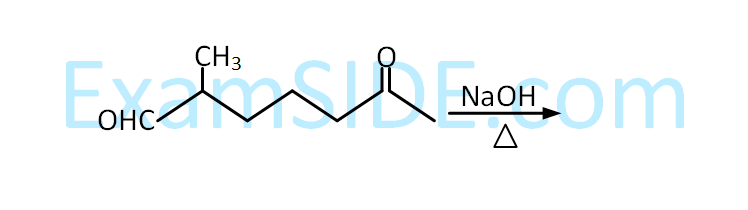

6
The correct statement about ICl5 and $$ICl_4^-$$ is
7
Which of the following compounds will show
the maximum 'enol' content?
8
5 moles of an ideal gas at 100 K are allowed
to undergo reversible compression till its
temperature becomes 200 K.
If CV = 28 JK–1mol–1, calculate $$\Delta $$U and $$\Delta $$pV for
this process. (R = 8.0 JK–1 mol–1]
9
The major product obtained in the following
reaction is :


10
The statement that is INCORRECT about the
interstitial compounds is :
11
For a reaction scheme $$A\buildrel {{k_1}} \over
\longrightarrow B\buildrel {{k_2}} \over
\longrightarrow C$$,
if the rate of formation of B is set to be zero then the concentration of B is given by :
if the rate of formation of B is set to be zero then the concentration of B is given by :
12
The major product of the following reaction is:
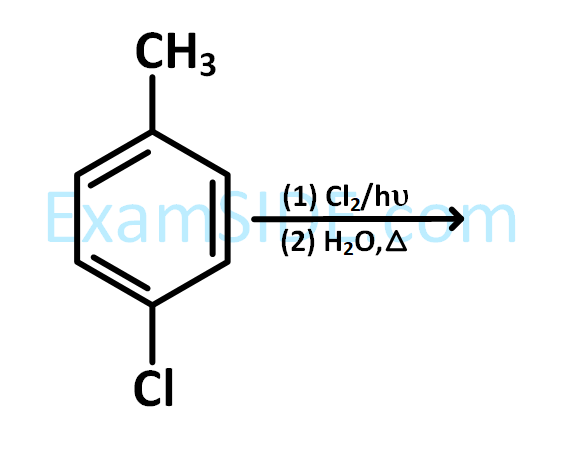

13
Among the following molecules / ions,
$$C_2^{2 - },N_2^{2 - },O_2^{2 - },{O_2}$$
which one is diamagnetic and has the shortest
bond length?
14
The calculated spin-only magnetic moments
(BM) of the anionic and cationic species of
[Fe(H2O)6]2 and [Fe(CN)6], respectively, are :
15
Which one of the following alkenes when
treated with HCl yields majorly an anti
Markovnikov product?
16
The covalent alkaline earth metal halide
(X = Cl, Br, I) is :
17
The compound that inhibits the growth of
tumors is :
18
The IUPAC symbol for the element with atomic
number 119 would be :
19
The percentage composition of carbon by mole
in methane is :
20
The major product of the following reaction is:
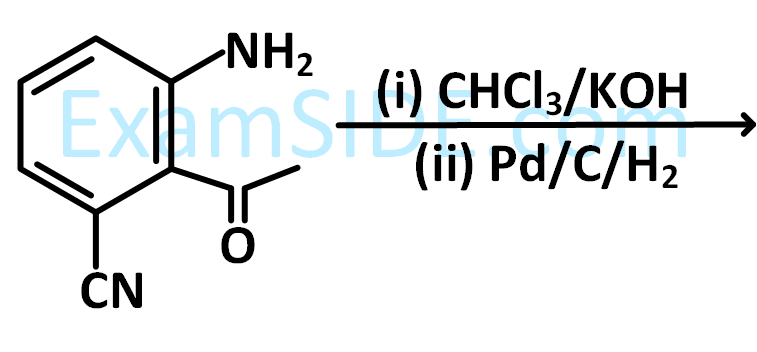

21
The ion that has sp3d2 hybridization for the
central atom, is :
22
For the following reactions, equilibrium
constants are given :
S(s) + O2(g) ⇋ SO2(g); K1 = 1052
2S(s) + 3O2(g) ⇋ 2SO3(g); K2 = 10129
The equilibrium constant for the reaction,
2SO2(g) + O2(g) ⇋ 2SO3(g) is :
S(s) + O2(g) ⇋ SO2(g); K1 = 1052
2S(s) + 3O2(g) ⇋ 2SO3(g); K2 = 10129
The equilibrium constant for the reaction,
2SO2(g) + O2(g) ⇋ 2SO3(g) is :
23
The major product in the following reaction is :
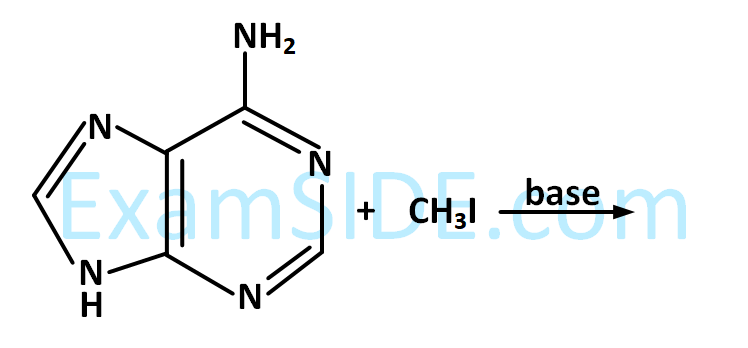

24
Calculate the standard cell potential in (V) of the
cell in which following reaction takes place :
Fe2+(aq) + Ag+(aq) $$ \to $$ Fe3+(aq) + Ag (s)
Given that
$$E_{A{g^ + }/Ag}^o = xV$$
$$E_{Fe^{2+ }/Fe}^o = yV$$
$$E_{Fe^{3+ }/Fe}^o = zV$$
Fe2+(aq) + Ag+(aq) $$ \to $$ Fe3+(aq) + Ag (s)
Given that
$$E_{A{g^ + }/Ag}^o = xV$$
$$E_{Fe^{2+ }/Fe}^o = yV$$
$$E_{Fe^{3+ }/Fe}^o = zV$$
Mathematics
1
Let $$\mathop a\limits^ \to = 3\mathop i\limits^ \wedge + 2\mathop j\limits^ \wedge + x\mathop k\limits^ \wedge $$ and $$\mathop b\limits^ \to = \mathop i\limits^ \wedge - \mathop j\limits^ \wedge + \mathop k\limits^ \wedge $$
, for some real x. Then $$\left| {\mathop a\limits^ \to \times \mathop b\limits^ \to } \right|$$ = r
is possible if :
2
In an ellipse, with centre at the origin, if the
difference of the lengths of major axis and minor
axis is 10 and one of the foci is at (0,5$$\sqrt 3$$), then
the length of its latus rectum is :
3
If $$z = {{\sqrt 3 } \over 2} + {i \over 2}\left( {i = \sqrt { - 1} } \right)$$,
then (1 + iz + z5 + iz8)9 is equal to :
then (1 + iz + z5 + iz8)9 is equal to :
4
Let $$f(x) = \int\limits_0^x {g(t)dt} $$ where g is a non-zero even
function. If ƒ(x + 5) = g(x), then $$ \int\limits_0^x {f(t)dt} $$ equals-
5
If three distinct numbers a, b, c are in G.P. and the
equations ax2
+ 2bx + c = 0 and
dx2
+ 2ex + ƒ = 0 have a common root, then
which one of the following statements is
correct?
6
The number of integral values of m for which the
equation
(1 + m2 )x2 – 2(1 + 3m)x + (1 + 8m) = 0 has no real root is :
(1 + m2 )x2 – 2(1 + 3m)x + (1 + 8m) = 0 has no real root is :
7
If a point R(4, y, z) lies on the line segment joining
the points P(2, –3, 4) and Q(8, 0, 10), then the
distance of R from the origin is :
8
Let the number 2,b,c be in an A.P. and
A = $$\left[ {\matrix{ 1 & 1 & 1 \cr 2 & b & c \cr 4 & {{b^2}} & {{c^2}} \cr } } \right]$$. If det(A) $$ \in $$ [2, 16], then c lies in the interval :
A = $$\left[ {\matrix{ 1 & 1 & 1 \cr 2 & b & c \cr 4 & {{b^2}} & {{c^2}} \cr } } \right]$$. If det(A) $$ \in $$ [2, 16], then c lies in the interval :
9
Let ƒ : R $$ \to $$ R be a differentiable function
satisfying ƒ'(3) + ƒ'(2) = 0.
Then $$\mathop {\lim }\limits_{x \to 0} {\left( {{{1 + f(3 + x) - f(3)} \over {1 + f(2 - x) - f(2)}}} \right)^{{1 \over x}}}$$ is equal to
Then $$\mathop {\lim }\limits_{x \to 0} {\left( {{{1 + f(3 + x) - f(3)} \over {1 + f(2 - x) - f(2)}}} \right)^{{1 \over x}}}$$ is equal to
10
If the fourth term in the binomial expansion of
$${\left( {\sqrt {{x^{\left( {{1 \over {1 + {{\log }_{10}}x}}} \right)}}} + {x^{{1 \over {12}}}}} \right)^6}$$ is equal to 200, and x > 1, then the value of x is :
$${\left( {\sqrt {{x^{\left( {{1 \over {1 + {{\log }_{10}}x}}} \right)}}} + {x^{{1 \over {12}}}}} \right)^6}$$ is equal to 200, and x > 1, then the value of x is :
11
If ƒ(1) = 1, ƒ'(1) = 3, then the derivative of
ƒ(ƒ(ƒ(x))) + (ƒ(x))2
at x = 1 is :
12
Let S($$\alpha $$) = {(x, y) : y2
$$ \le $$ x, 0 $$ \le $$ x $$ \le $$ $$\alpha $$} and A($$\alpha $$)
is area of the region S($$\alpha $$). If for a $$\lambda $$, 0 < $$\lambda $$ < 4,
A($$\lambda $$) : A(4) = 2 : 5, then $$\lambda $$ equals
13
If the system of linear equations
x – 2y + kz = 1
2x + y + z = 2
3x – y – kz = 3
has a solution (x,y,z), z $$ \ne $$ 0, then (x,y) lies on the straight line whose equation is :
x – 2y + kz = 1
2x + y + z = 2
3x – y – kz = 3
has a solution (x,y,z), z $$ \ne $$ 0, then (x,y) lies on the straight line whose equation is :
14
Let ƒ(x) = ax
(a > 0) be written as
ƒ(x) = ƒ1 (x) + ƒ2 (x), where ƒ1 (x) is an even function of ƒ2 (x) is an odd function.
Then ƒ1 (x + y) + ƒ1 (x – y) equals
ƒ(x) = ƒ1 (x) + ƒ2 (x), where ƒ1 (x) is an even function of ƒ2 (x) is an odd function.
Then ƒ1 (x + y) + ƒ1 (x – y) equals
15
A student scores the following marks in five tests
:
45, 54, 41, 57, 43.
His score is not known for the sixth test. If the mean score is 48 in the six tests, then the standard deviation of the marks in six tests is
45, 54, 41, 57, 43.
His score is not known for the sixth test. If the mean score is 48 in the six tests, then the standard deviation of the marks in six tests is
16
The minimum number of times one has to toss a
fair coin so that the probability of observing at least
one head is at least 90% is :
17
The height of a right circular cylinder of maximum
volume inscribed in a sphere of radius 3 is
18
The number of four-digit numbers strictly greater
than 4321 that can be formed using the digits
0,1,2,3,4,5 (repetition of digits is allowed) is :
19
Let ƒ : [–1,3] $$ \to $$ R be defined as
$$f(x) = \left\{ {\matrix{ {\left| x \right| + \left[ x \right]} & , & { - 1 \le x < 1} \cr {x + \left| x \right|} & , & {1 \le x < 2} \cr {x + \left[ x \right]} & , & {2 \le x \le 3} \cr } } \right.$$
where [t] denotes the greatest integer less than or equal to t. Then, ƒ is discontinuous at:
$$f(x) = \left\{ {\matrix{ {\left| x \right| + \left[ x \right]} & , & { - 1 \le x < 1} \cr {x + \left| x \right|} & , & {1 \le x < 2} \cr {x + \left[ x \right]} & , & {2 \le x \le 3} \cr } } \right.$$
where [t] denotes the greatest integer less than or equal to t. Then, ƒ is discontinuous at:
20
Suppose that the points (h,k), (1,2) and (–3,4) lie
on the line L1
. If a line L2
passing through the points
(h,k) and (4,3) is perpendicular to L1
, then
$$k \over h$$
equals :
21
If $$\int {{{dx} \over {{x^3}{{(1 + {x^6})}^{2/3}}}} = xf(x){{(1 + {x^6})}^{{1 \over 3}}} + C} $$
where C is a constant of integration, then the function ƒ(x) is equal to
where C is a constant of integration, then the function ƒ(x) is equal to
Physics
1
A cell of internal resistance r drives current
through an external resistance R. The power
delivered by the cell to the external resistance
will be maximum when :-
2
An electric dipole is formed by two equal and
opposite charges q with separation d. The
charges have same mass m. It is kept in a
uniform electric field E. If it is slightly rotated
from its equilibrium orientation, then its angular
frequency $$\omega$$ is :-
3
A particle starts from origin O from rest and
moves with a uniform acceleration along the
positive x-axis. Identify all figures that
correctly represent the motion qualitatively.
(a = acceleration, v = velocity,
x = displacement, t = time)
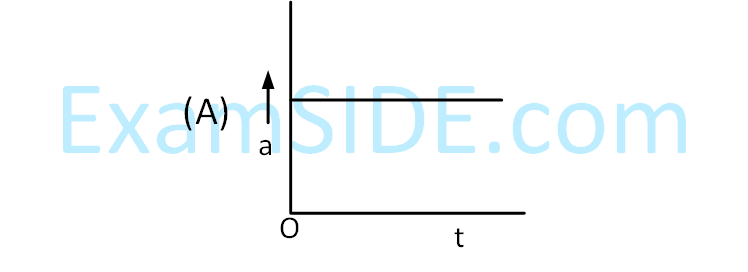
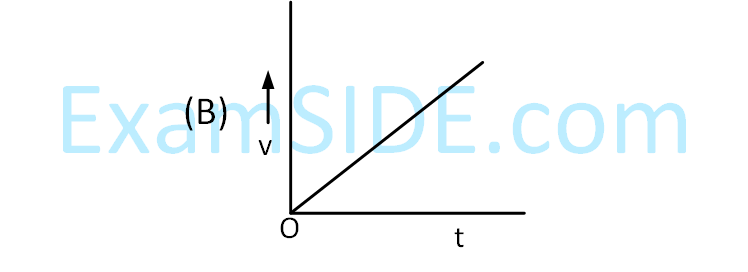
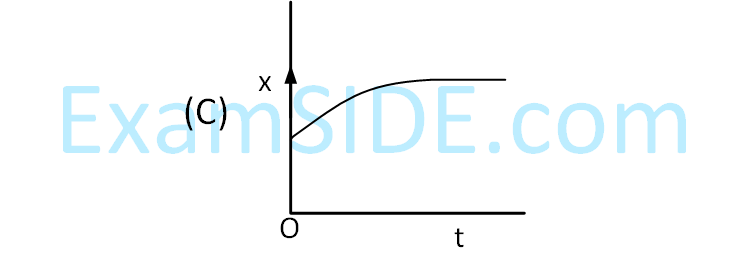
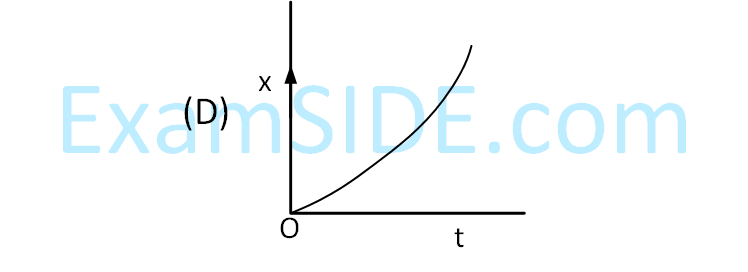


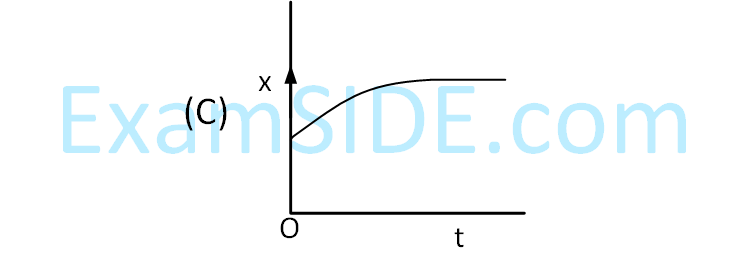
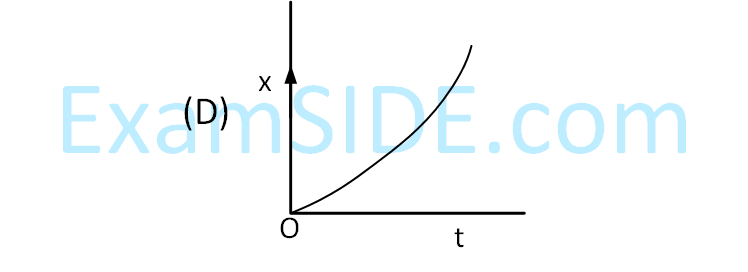
4
Two very long, straight, and insulated wires are
kept at 90° angle from each other in xy-plane
as shown in the figure. These wires carry
currents of equal magnitude I, whose directions
are shown in the figure. The net magnetic field
at point P will be :
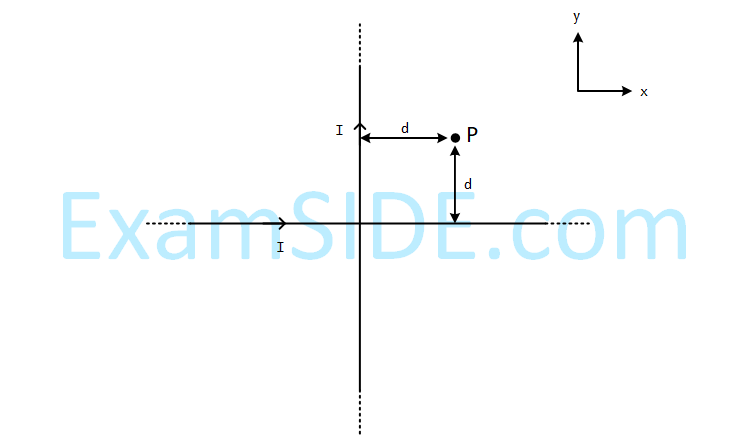

5
A circuit connected to an ac source of emf
e = e0sin(100t) with t in seconds, gives a phase
difference of $$\pi $$/4 between the emf e and
current i. Which of the following circuits will
exhibit this ?
6
The magnetic field of an electromagnetic wave
is given by :-
$$\mathop B\limits^ \to = 1.6 \times {10^{ - 6}}\cos \left( {2 \times {{10}^7}z + 6 \times {{10}^{15}}t} \right)\left( {2\mathop i\limits^ \wedge + \mathop j\limits^ \wedge } \right){{Wb} \over {{m^2}}}$$
The associated electric field will be :-
$$\mathop B\limits^ \to = 1.6 \times {10^{ - 6}}\cos \left( {2 \times {{10}^7}z + 6 \times {{10}^{15}}t} \right)\left( {2\mathop i\limits^ \wedge + \mathop j\limits^ \wedge } \right){{Wb} \over {{m^2}}}$$
The associated electric field will be :-
7
In a simple pendulum experiment for
determination of acceleration due to gravity (g),
time taken for 20 oscillations is measured by
using a watch of 1 second least count. The
mean value of time taken comes out to be
30 s. The length of pendulum is measured by
using a meter scale of least count 1 mm and the
value obtained is 55.0 cm. The percentage
error in the determination of g is close to :-
8
Two magnetic dipoles X and Y are placed at
a separation d, with their axes perpendicular to
each other. The dipole moment of Y is twice
that of X. A particle of charge q is passing,
through their midpoint P, at angle q = 45° with
the horizontal line, as shown in figure. What
would be the magnitude of force on the particle
at that instant ?
(d is much larger than the dimensions of the dipole)
(d is much larger than the dimensions of the dipole)

9
Let $$\left| {\mathop {{A_1}}\limits^ \to } \right| = 3$$, $$\left| {\mathop {{A_2}}\limits^ \to } \right| = 5$$ and $$\left| {\mathop {{A_1}}\limits^ \to + \mathop {{A_2}}\limits^ \to } \right| = 5$$. The
value of $$\left( {2\mathop {{A_1}}\limits^ \to + 3\mathop {{A_2}}\limits^ \to } \right)\left( {3\mathop {{A_1}}\limits^ \to - \mathop {2{A_2}}\limits^ \to } \right)$$
is :-
10
A nucleus A, with a finite de-broglie
wavelength $$\lambda $$A, undergoes spontaneous fission
into two nuclei B and C of equal mass. B flies
in the same direction as that of A, while C flies
in the opposite direction with a velocity equal
to half of that of B. The de-Broglie wavelengths
$$\lambda $$B and $$\lambda $$C of B and C are respectively :
11
A body of mass m1 moving with an unknown
velocity of $${v_1}\mathop i\limits^ \wedge $$, undergoes a collinear collision
with a body of mass m2 moving with a velocity
$${v_2}\mathop i\limits^ \wedge $$ . After collision, m1 and m2 move with
velocities of $${v_3}\mathop i\limits^ \wedge $$ and $${v_4}\mathop i\limits^ \wedge $$ , respectively.
If m2 = 0.5 m1 and v3 = 0.5 v1, then v1 is :-
12
In the figure shown, what is the current
(in Ampere) drawn from the battery ?
You are given: R1 = 15$$\Omega $$, R2 = 10 $$\Omega $$, R3 = 20 $$\Omega $$, R4 = 5$$\Omega $$, R5 = 25$$\Omega $$, R6 = 30 $$\Omega $$, E = 15 V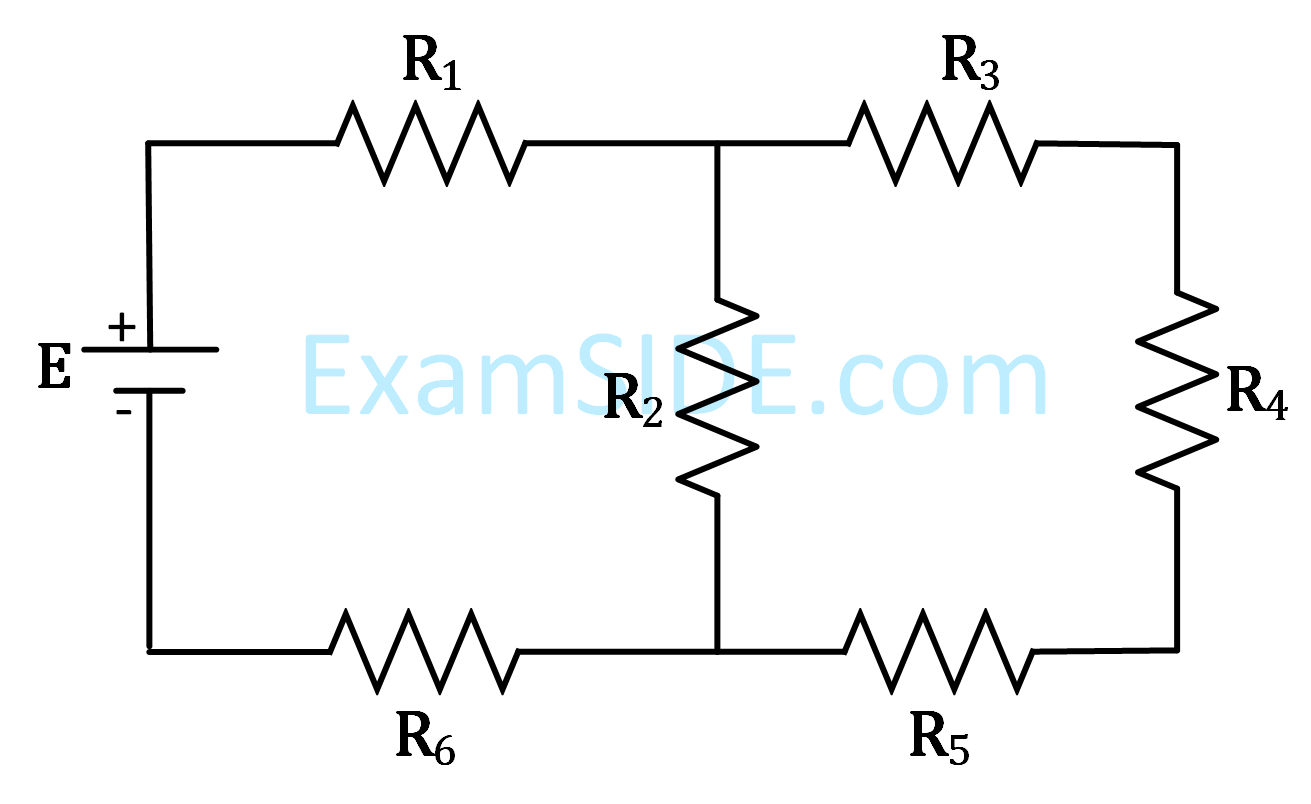
You are given: R1 = 15$$\Omega $$, R2 = 10 $$\Omega $$, R3 = 20 $$\Omega $$, R4 = 5$$\Omega $$, R5 = 25$$\Omega $$, R6 = 30 $$\Omega $$, E = 15 V

13
If surface tension (S), Moment of inertia (I) and
Planck's constant (h), were to be taken as the
fundamental units, the dimensional formula for
linear momentum would be :-
14
A convex lens (of focal length 20 cm) and a
concave mirror, having their principal axes
along the same lines, are kept 80 cm apart from
each other. The concave mirror is to the right
of the convex lens. When an object is kept at
a distance of 30 cm to the left of the convex
lens, its image remains at the same position
even if the concave mirror is removed. The
maximum distance of the object for which this
concave mirror, by itself would produce a
virtual image would be :-
15
A rectangular solid box of length 0.3 m is held
horizontally, with one of its sides on the edge
of a platform of height 5m. When released, it
slips off the table in a very short time t = 0.01s,
remaining essentially horizontal. The angle by
which it would rotate when it hits the ground
will be (in radians) close to :-
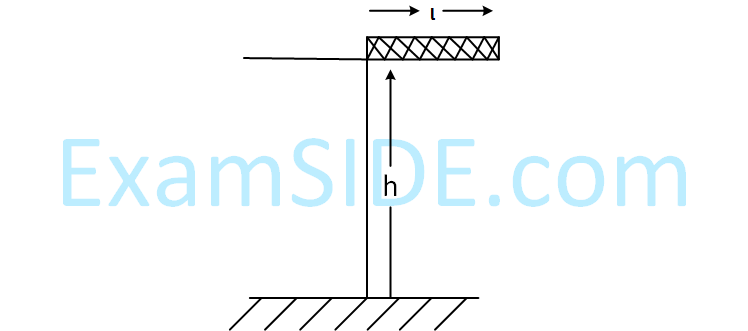

16
The temperature, at which the root mean square
velocity of hydrogen molecules equals their
escape velocity from the earth, is closest to :
[Boltzmann Constant kB = 1.38 × 10–23 J/K Avogadro Number NA = 6.02 × 1026 /kg Radius of Earth : 6.4 × 106 m Gravitational acceleration on Earth = 10ms–2]
[Boltzmann Constant kB = 1.38 × 10–23 J/K Avogadro Number NA = 6.02 × 1026 /kg Radius of Earth : 6.4 × 106 m Gravitational acceleration on Earth = 10ms–2]
17
A uniform rectangular thin sheet ABCD of
mass M has length a and breadth b, as shown
in the figure. If the shaded portion HBGO is
cut-off, the coordinates of the centre of mass
of the remaining portion will be :-
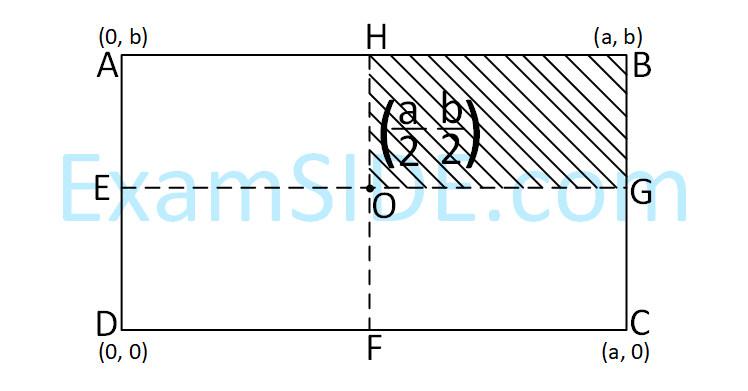

18
A parallel plate capacitor has 1μF capacitance.
One of its two plates is given +2μC charge and
the other plate, +4μC charge. The potential
difference developed across the capacitor is:-
19
The electric field in a region is given by
$$\mathop E\limits^ \to = \left( {Ax + B} \right)\mathop i\limits^ \wedge $$
, where E is in NC–1 and x is in
metres. The values of constants are
A = 20 SI unit and B = 10 SI unit. If the potential
at x = 1 is V1 and that at x = –5 is V2, then
V1 – V2 is :-
20
A positive point charge is released from rest at
a distance r0 from a positive line charge with
uniform density. The speed (v) of the point
charge, as a function of instantaneous distance
r from line charge, is proportional to :-
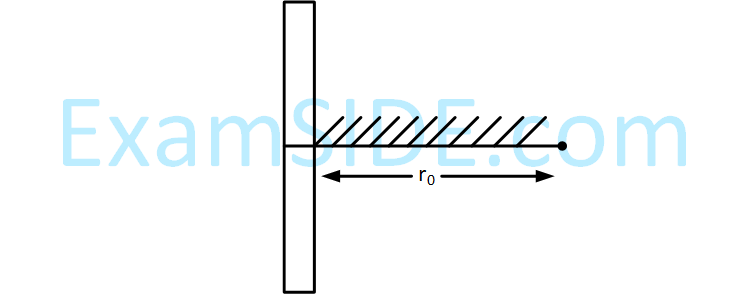

21
The given diagram shows four processes i.e.,
isochoric, isobaric, isothermal and adiabatic.
The correct assignment of the processes, in the
same order is given by :-
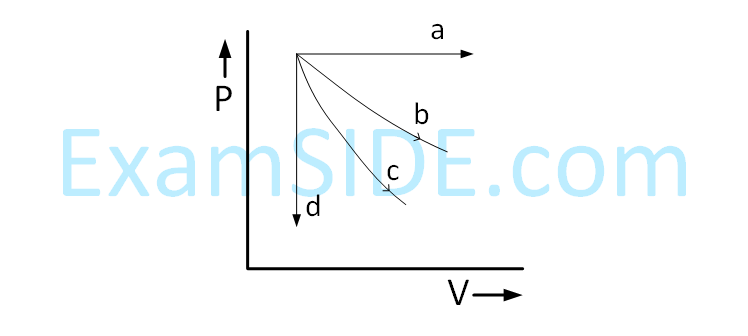

22
A rocket has to be launched from earth in such
a way that it never returns. If E is the minimum
energy delivered by the rocket launcher, what
should be the minimum energy that the
launcher should have if the same rocket is to
be launched from the surface of the moon ?
Assume that the density of the earth and the
moon are equal and that the earth's volume is
64 times the volume of the moon :-
23
A solid sphere and solid cylinder of identical
radii approach an incline with the same linear
velocity (see figure). Both roll without slipping
all throughout. The two climb maximum
heights hsph and hcyl on the incline. The ratio
hsph/hcyl is given by :-


24
Young's moduli of two wires A and B are in the
ratio 7 : 4. Wire A is 2 m long and has radius R.
Wire B is 1.5 m long and has radius 2 mm. If
the two wires stretch by the same length for a
given load, then the value of R is close to :-
25
The ratio of mass densities of nuclei of 40Ca
and 16O is close to :-
26
Calculate the limit of resolution of a telescope
objective having a diameter of 200 cm, if it has
to detect light of wavelength 500 nm coming
from a star :-