2025
JEE Main 2025 (Online) 8th April Evening ShiftJEE Main 2025 (Online) 7th April Evening ShiftJEE Main 2025 (Online) 7th April Morning ShiftJEE Main 2025 (Online) 4th April Evening ShiftJEE Main 2025 (Online) 4th April Morning ShiftJEE Main 2025 (Online) 3rd April Evening ShiftJEE Main 2025 (Online) 3rd April Morning ShiftJEE Main 2025 (Online) 2nd April Evening ShiftJEE Main 2025 (Online) 2nd April Morning ShiftJEE Main 2025 (Online) 29th January Evening ShiftJEE Main 2025 (Online) 29th January Morning ShiftJEE Main 2025 (Online) 28th January Evening ShiftJEE Main 2025 (Online) 28th January Morning ShiftJEE Main 2025 (Online) 24th January Evening ShiftJEE Main 2025 (Online) 24th January Morning ShiftJEE Main 2025 (Online) 23rd January Evening ShiftJEE Main 2025 (Online) 23rd January Morning ShiftJEE Main 2025 (Online) 22nd January Evening ShiftJEE Main 2025 (Online) 22nd January Morning Shift2024
JEE Main 2024 (Online) 9th April Evening ShiftJEE Main 2024 (Online) 9th April Morning ShiftJEE Main 2024 (Online) 8th April Evening ShiftJEE Main 2024 (Online) 8th April Morning ShiftJEE Main 2024 (Online) 6th April Evening ShiftJEE Main 2024 (Online) 6th April Morning ShiftJEE Main 2024 (Online) 5th April Evening ShiftJEE Main 2024 (Online) 5th April Morning ShiftJEE Main 2024 (Online) 4th April Evening ShiftJEE Main 2024 (Online) 4th April Morning ShiftJEE Main 2024 (Online) 1st February Evening ShiftJEE Main 2024 (Online) 1st February Morning ShiftJEE Main 2024 (Online) 31st January Evening ShiftJEE Main 2024 (Online) 31st January Morning ShiftJEE Main 2024 (Online) 30th January Evening ShiftJEE Main 2024 (Online) 30th January Morning ShiftJEE Main 2024 (Online) 29th January Evening ShiftJEE Main 2024 (Online) 29th January Morning ShiftJEE Main 2024 (Online) 27th January Evening ShiftJEE Main 2024 (Online) 27th January Morning Shift2023
JEE Main 2023 (Online) 15th April Morning ShiftJEE Main 2023 (Online) 13th April Evening ShiftJEE Main 2023 (Online) 13th April Morning ShiftJEE Main 2023 (Online) 12th April Morning ShiftJEE Main 2023 (Online) 11th April Evening ShiftJEE Main 2023 (Online) 11th April Morning ShiftJEE Main 2023 (Online) 10th April Evening ShiftJEE Main 2023 (Online) 10th April Morning ShiftJEE Main 2023 (Online) 8th April Evening ShiftJEE Main 2023 (Online) 8th April Morning ShiftJEE Main 2023 (Online) 6th April Evening ShiftJEE Main 2023 (Online) 6th April Morning ShiftJEE Main 2023 (Online) 1st February Evening ShiftJEE Main 2023 (Online) 1st February Morning ShiftJEE Main 2023 (Online) 31st January Evening ShiftJEE Main 2023 (Online) 31st January Morning ShiftJEE Main 2023 (Online) 30th January Evening ShiftJEE Main 2023 (Online) 30th January Morning ShiftJEE Main 2023 (Online) 29th January Evening ShiftJEE Main 2023 (Online) 29th January Morning ShiftJEE Main 2023 (Online) 25th January Evening ShiftJEE Main 2023 (Online) 25th January Morning ShiftJEE Main 2023 (Online) 24th January Evening ShiftJEE Main 2023 (Online) 24th January Morning Shift2022
JEE Main 2022 (Online) 29th July Evening ShiftJEE Main 2022 (Online) 29th July Morning ShiftJEE Main 2022 (Online) 28th July Evening ShiftJEE Main 2022 (Online) 28th July Morning ShiftJEE Main 2022 (Online) 27th July Evening ShiftJEE Main 2022 (Online) 27th July Morning ShiftJEE Main 2022 (Online) 26th July Evening ShiftJEE Main 2022 (Online) 26th July Morning ShiftJEE Main 2022 (Online) 25th July Evening ShiftJEE Main 2022 (Online) 25th July Morning ShiftJEE Main 2022 (Online) 30th June Morning ShiftJEE Main 2022 (Online) 29th June Evening ShiftJEE Main 2022 (Online) 29th June Morning ShiftJEE Main 2022 (Online) 28th June Evening ShiftJEE Main 2022 (Online) 28th June Morning ShiftJEE Main 2022 (Online) 27th June Evening ShiftJEE Main 2022 (Online) 27th June Morning ShiftJEE Main 2022 (Online) 26th June Evening ShiftJEE Main 2022 (Online) 26th June Morning ShiftJEE Main 2022 (Online) 25th June Evening ShiftJEE Main 2022 (Online) 25th June Morning ShiftJEE Main 2022 (Online) 24th June Evening ShiftJEE Main 2022 (Online) 24th June Morning Shift2021
JEE Main 2021 (Online) 1st September Evening ShiftJEE Main 2021 (Online) 31st August Evening ShiftJEE Main 2021 (Online) 31st August Morning ShiftJEE Main 2021 (Online) 27th August Evening ShiftJEE Main 2021 (Online) 27th August Morning ShiftJEE Main 2021 (Online) 26th August Evening ShiftJEE Main 2021 (Online) 26th August Morning ShiftJEE Main 2021 (Online) 27th July Evening ShiftJEE Main 2021 (Online) 27th July Morning ShiftJEE Main 2021 (Online) 25th July Evening ShiftJEE Main 2021 (Online) 25th July Morning ShiftJEE Main 2021 (Online) 22th July Evening ShiftJEE Main 2021 (Online) 20th July Evening ShiftJEE Main 2021 (Online) 20th July Morning ShiftJEE Main 2021 (Online) 18th March Evening ShiftJEE Main 2021 (Online) 18th March Morning ShiftJEE Main 2021 (Online) 17th March Evening ShiftJEE Main 2021 (Online) 17th March Morning ShiftJEE Main 2021 (Online) 16th March Evening ShiftJEE Main 2021 (Online) 16th March Morning ShiftJEE Main 2021 (Online) 26th February Evening ShiftJEE Main 2021 (Online) 26th February Morning ShiftJEE Main 2021 (Online) 25th February Evening ShiftJEE Main 2021 (Online) 25th February Morning ShiftJEE Main 2021 (Online) 24th February Evening ShiftJEE Main 2021 (Online) 24th February Morning Shift2020
JEE Main 2020 (Online) 6th September Evening SlotJEE Main 2020 (Online) 6th September Morning SlotJEE Main 2020 (Online) 5th September Evening SlotJEE Main 2020 (Online) 5th September Morning SlotJEE Main 2020 (Online) 4th September Evening SlotJEE Main 2020 (Online) 4th September Morning SlotJEE Main 2020 (Online) 3rd September Evening SlotJEE Main 2020 (Online) 3rd September Morning SlotJEE Main 2020 (Online) 2nd September Evening SlotJEE Main 2020 (Online) 2nd September Morning SlotJEE Main 2020 (Online) 9th January Evening SlotJEE Main 2020 (Online) 9th January Morning SlotJEE Main 2020 (Online) 8th January Evening SlotJEE Main 2020 (Online) 8th January Morning SlotJEE Main 2020 (Online) 7th January Evening SlotJEE Main 2020 (Online) 7th January Morning Slot2019
JEE Main 2019 (Online) 12th April Evening SlotJEE Main 2019 (Online) 12th April Morning SlotJEE Main 2019 (Online) 10th April Evening SlotJEE Main 2019 (Online) 10th April Morning SlotJEE Main 2019 (Online) 9th April Evening SlotJEE Main 2019 (Online) 9th April Morning SlotJEE Main 2019 (Online) 8th April Evening SlotJEE Main 2019 (Online) 8th April Morning SlotJEE Main 2019 (Online) 12th January Evening SlotJEE Main 2019 (Online) 12th January Morning SlotJEE Main 2019 (Online) 11th January Evening SlotJEE Main 2019 (Online) 11th January Morning SlotJEE Main 2019 (Online) 10th January Evening SlotJEE Main 2019 (Online) 10th January Morning SlotJEE Main 2019 (Online) 9th January Evening SlotJEE Main 2019 (Online) 9th January Morning Slot2018
JEE Main 2018 (Online) 16th April Morning SlotJEE Main 2018 (Offline)JEE Main 2018 (Online) 15th April Evening SlotJEE Main 2018 (Online) 15th April Morning Slot2017
JEE Main 2017 (Online) 9th April Morning SlotJEE Main 2017 (Online) 8th April Morning SlotJEE Main 2017 (Offline)2016
JEE Main 2016 (Online) 10th April Morning SlotJEE Main 2016 (Online) 9th April Morning SlotJEE Main 2016 (Offline)2015
JEE Main 2015 (Offline)2014
JEE Main 2014 (Offline)2013
JEE Main 2013 (Offline)2012
AIEEE 20122011
AIEEE 20112010
AIEEE 20102009
AIEEE 20092008
AIEEE 20082007
AIEEE 20072006
AIEEE 20062005
AIEEE 20052004
AIEEE 20042003
AIEEE 20032002
AIEEE 2002JEE Main 2017 (Offline)
Paper was held on Sun, Apr 2, 2017 9:30 AM
Chemistry
1
The major product obtained in the following reaction is :


2
Which of the following compounds will behave as a reducing sugar in an aqueous KOH solution?
3
The correct sequence of reagents for the following conversion will be :


4
Sodium salt of an organic acid ‘X’ produces effervescence with conc. H2SO4. ‘X’ reacts with the acidified
aqueous CaCl2 solution to give a white precipitate which decolourises acidic solution of KMnO4. ‘X’ is :
5
The major product obtained in the following reaction is :


6
3-Methyl-pent-2-ene on reaction with HBr in presence of peroxide forms an addition product. The number
of possible stereoisomers for the product is :
7
Which of the following, upon treatment with tert-BuONa followed by addition of bromine water, fails to
decolorize the colour of bromine?
8
The increasing order of the reactivity of the following halides for the SN1 reaction is :


9
Which of the following compounds will form significant amount of meta product during mono-nitration
reaction?
10
Which of the following molecules is least resonance stabilized?
11
In the following reactions, ZnO is respectively acting as a/an :
(a) ZnO + Na2O $$\to$$ Na2ZnO2
(b) ZnO + CO2 $$\to$$ ZnCO3
(a) ZnO + Na2O $$\to$$ Na2ZnO2
(b) ZnO + CO2 $$\to$$ ZnCO3
12
On treatment of 100 mL of 0.1 M solution of CoCl3. 6H2O with excess AgNO3; 1.2 $$\times$$ 1022 ions are precipitated. The complex is :
13
The most abundant elements by mass in the body of a healthy human adult are: Oxygen (61.4%); Carbon
(22.9%), Hydrogen (10.0%); and Nitrogen (2.6%). The weight which a 75 kg person would gain if all
1H atoms are replaced by 2H atoms is:
14
pKa of a weak acid (HA) and pKb of a weak base (BOH) are 3.2 and 3.4, respectively. The pH of their salt (AB) solution is :
15
Which of the following reactions is an example of a redox reaction?
16
Given
$$E_{C{l_2}/C{l^ - }}^o$$ = 1.36 V, $$E_{C{r^{3 + }}/Cr}^o$$ = - 0.74 V
$$E_{C{r_2}{O_7}^{2 - }/C{r^{3 + }}}^o$$ = 1.33 V, $$E_{Mn{O_4}^ - /Mn ^{2+}}^o$$ = 1.51 V
Among the following, the strongest reducing agent is :
$$E_{C{l_2}/C{l^ - }}^o$$ = 1.36 V, $$E_{C{r^{3 + }}/Cr}^o$$ = - 0.74 V
$$E_{C{r_2}{O_7}^{2 - }/C{r^{3 + }}}^o$$ = 1.33 V, $$E_{Mn{O_4}^ - /Mn ^{2+}}^o$$ = 1.51 V
Among the following, the strongest reducing agent is :
17
Two reactions R1 and R2 have identical pre-exponential factors. Activation energy of R1 exceeds that of R2 by 10 kJ mol–1. If k1 and k2 are rate constants for reactions R1 and R2 respectively at 300 K, then ln(k2/k1) is equal to :
(R = 8.314 J mol–1 K–1)
(R = 8.314 J mol–1 K–1)
18
The freezing point of benzene decreases by 0.450C when 0.2 g of acetic acid is added to 20g of benzene. If
acetic acid associates to form a dimer in benzene, percentage association of acetic acid in benzene will be:
(Kf for benzene = 5.12 K kg mol–1)
19
$$\Delta $$U is equal to :
20
The group having isoelectronic species is:
21
Given, $${C_{(graphite)}} + {O_2} \to C{O_2}(g)$$;
$${\Delta _r}{H^o}$$ = - 393.5 kJ mol-1
$${{\rm H}_2}(g)$$ + $${1 \over 2}{O_2}(g)$$$$\to {{\rm H}_2}{\rm O}(l)$$
$${\Delta _r}{H^o}$$ = - 285.8 kJ mol-1
$$C{O_2}(g)$$ + $$2{{\rm H}_2}{\rm O}(l) \to$$ $$C{H_4}(g)$$ + $$2{O_2}(g)$$
$${\Delta _r}{H^o}$$ = + 890.3 kJ mol-1
Based on the above thermochemical equations, the value of $${\Delta _r}{H^o}$$ at 298 K for the reaction
$${C_{(graphite)}}$$ + $$2{{\rm H}_2}(g) \to$$ $$C{H_4}(g)$$ will be :
$${\Delta _r}{H^o}$$ = - 393.5 kJ mol-1
$${{\rm H}_2}(g)$$ + $${1 \over 2}{O_2}(g)$$$$\to {{\rm H}_2}{\rm O}(l)$$
$${\Delta _r}{H^o}$$ = - 285.8 kJ mol-1
$$C{O_2}(g)$$ + $$2{{\rm H}_2}{\rm O}(l) \to$$ $$C{H_4}(g)$$ + $$2{O_2}(g)$$
$${\Delta _r}{H^o}$$ = + 890.3 kJ mol-1
Based on the above thermochemical equations, the value of $${\Delta _r}{H^o}$$ at 298 K for the reaction
$${C_{(graphite)}}$$ + $$2{{\rm H}_2}(g) \to$$ $$C{H_4}(g)$$ will be :
22
The radius of the second Bohr orbit for hydrogen atom is:
(Planck’s Const. h = 6.6262 × 10-34 Js; mass of electron = 9.1091 × 10-31 kg; charge of electron (e) = 1.60210 × 10-19 C; permittivity of vacuum ($${\varepsilon _0}$$) = 8.854185 × 10-12 kg-1 m-3 A2)
(Planck’s Const. h = 6.6262 × 10-34 Js; mass of electron = 9.1091 × 10-31 kg; charge of electron (e) = 1.60210 × 10-19 C; permittivity of vacuum ($${\varepsilon _0}$$) = 8.854185 × 10-12 kg-1 m-3 A2)
23
Which of the following species is not paramagnetic?
24
1 gram of a carbonate (M2CO3) on treatment with excess HCl produces 0.01186 mole of CO2. The molar mass of M2CO3 in g mol–1 is:
Mathematics
1
Let $$a$$, b, c $$ \in R$$. If $$f$$(x) = ax2 + bx + c is such that
$$a$$ + b + c = 3 and $$f$$(x + y) = $$f$$(x) + $$f$$(y) + xy, $$\forall x,y \in R,$$
then $$\sum\limits_{n = 1}^{10} {f(n)} $$ is equal to
$$a$$ + b + c = 3 and $$f$$(x + y) = $$f$$(x) + $$f$$(y) + xy, $$\forall x,y \in R,$$
then $$\sum\limits_{n = 1}^{10} {f(n)} $$ is equal to
2
A man X has 7 friends, 4 of them are ladies and 3 are men. His wife Y also has 7 friends, 3 of them are
ladies and 4 are men. Assume X and Y have no common friends. Then the total number of ways in which X
and Y together can throw a party inviting 3 ladies and 3 men, so that 3 friends of each of X and Y are in
this party, is:
3
If for a positive integer n, the quadratic equation
$$x\left( {x + 1} \right) + \left( {x + 1} \right)\left( {x + 2} \right)$$$$ + .... + \left( {x + \overline {n - 1} } \right)\left( {x + n} \right)$$$$ = 10n$$
has two consecutive integral solutions, then n is equal to :
$$x\left( {x + 1} \right) + \left( {x + 1} \right)\left( {x + 2} \right)$$$$ + .... + \left( {x + \overline {n - 1} } \right)\left( {x + n} \right)$$$$ = 10n$$
has two consecutive integral solutions, then n is equal to :
4
If S is the set of distinct values of 'b' for which the following system of linear equations
x + y + z = 1
x + ay + z = 1
ax + by + z = 0
has no solution, then S is :
x + y + z = 1
x + ay + z = 1
ax + by + z = 0
has no solution, then S is :
5
If $$A = \left[ {\matrix{
2 & { - 3} \cr
{ - 4} & 1 \cr
} } \right]$$,
then adj(3A2 + 12A) is equal to
then adj(3A2 + 12A) is equal to
6
Let $$\omega $$ be a complex number such that 2$$\omega $$ + 1 = z where z = $$\sqrt {-3} $$. If
$$\left| {\matrix{ 1 & 1 & 1 \cr 1 & { - {\omega ^2} - 1} & {{\omega ^2}} \cr 1 & {{\omega ^2}} & {{\omega ^7}} \cr } } \right| = 3k$$,
then k is equal to :
$$\left| {\matrix{ 1 & 1 & 1 \cr 1 & { - {\omega ^2} - 1} & {{\omega ^2}} \cr 1 & {{\omega ^2}} & {{\omega ^7}} \cr } } \right| = 3k$$,
then k is equal to :
7
The function $$f:R \to \left[ { - {1 \over 2},{1 \over 2}} \right]$$ defined as
$$f\left( x \right) = {x \over {1 + {x^2}}}$$, is
$$f\left( x \right) = {x \over {1 + {x^2}}}$$, is
8
If $$5\left( {{{\tan }^2}x - {{\cos }^2}x} \right) = 2\cos 2x + 9$$,
then the value of $$\cos 4x$$ is :
then the value of $$\cos 4x$$ is :
9
For three events A, B and C,
P(Exactly one of A or B occurs)
= P(Exactly one of B or C occurs)
= P (Exactly one of C or A occurs) = $${1 \over 4}$$
and P(All the three events occur simultaneously) = $${1 \over {16}}$$.
Then the probability that at least one of the events occurs, is :
P(Exactly one of A or B occurs)
= P(Exactly one of B or C occurs)
= P (Exactly one of C or A occurs) = $${1 \over 4}$$
and P(All the three events occur simultaneously) = $${1 \over {16}}$$.
Then the probability that at least one of the events occurs, is :
10
If two different numbers are taken from the set {0, 1, 2, 3, ........, 10}; then the probability that their sum as
well as absolute difference are both multiple of 4, is :
11
Let $$\overrightarrow a = 2\widehat i + \widehat j -2 \widehat k$$ and $$\overrightarrow b = \widehat i + \widehat j$$.
Let $$\overrightarrow c $$ be a vector such that $$\left| {\overrightarrow c - \overrightarrow a } \right| = 3$$,
$$\left| {\left( {\overrightarrow a \times \overrightarrow b } \right) \times \overrightarrow c } \right| = 3$$ and the angle between $$\overrightarrow c $$ and $\overrightarrow a \times \overrightarrow b$ is $$30^\circ $$.
Then $$\overrightarrow a .\overrightarrow c $$ is equal to :
Let $$\overrightarrow c $$ be a vector such that $$\left| {\overrightarrow c - \overrightarrow a } \right| = 3$$,
$$\left| {\left( {\overrightarrow a \times \overrightarrow b } \right) \times \overrightarrow c } \right| = 3$$ and the angle between $$\overrightarrow c $$ and $\overrightarrow a \times \overrightarrow b$ is $$30^\circ $$.
Then $$\overrightarrow a .\overrightarrow c $$ is equal to :
12
Let k be an integer such that the triangle with vertices (k, – 3k), (5, k) and (–k, 2) has area 28 sq. units. Then the orthocentre of this triangle is at the point :
13
If $$\left( {2 + \sin x} \right){{dy} \over {dx}} + \left( {y + 1} \right)\cos x = 0$$ and y(0) = 1,
then $$y\left( {{\pi \over 2}} \right)$$ is equal to :
then $$y\left( {{\pi \over 2}} \right)$$ is equal to :
14
The area (in sq. units) of the region
$$\left\{ {\left( {x,y} \right):x \ge 0,x + y \le 3,{x^2} \le 4y\,and\,y \le 1 + \sqrt x } \right\}$$ is
$$\left\{ {\left( {x,y} \right):x \ge 0,x + y \le 3,{x^2} \le 4y\,and\,y \le 1 + \sqrt x } \right\}$$ is
15
Let $${I_n} = \int {{{\tan }^n}x\,dx} ,\,\left( {n > 1} \right).$$
If $${I_4} + {I_6}$$ = $$a{\tan ^5}x + b{x^5} + C$$, where C is a constant of integration,
then the ordered pair $$\left( {a,b} \right)$$ is equal to
If $${I_4} + {I_6}$$ = $$a{\tan ^5}x + b{x^5} + C$$, where C is a constant of integration,
then the ordered pair $$\left( {a,b} \right)$$ is equal to
16
The integral $$\int\limits_{{\pi \over 4}}^{{{3\pi } \over 4}} {{{dx} \over {1 + \cos x}}} $$ is equal to
17
Twenty meters of wire is available for fencing off a flower-bed in the form of a circular sector. Then the
maximum area (in sq. m) of the flower-bed, is :
18
If for $$x \in \left( {0,{1 \over 4}} \right)$$, the derivatives of
$${\tan ^{ - 1}}\left( {{{6x\sqrt x } \over {1 - 9{x^3}}}} \right)$$ is $$\sqrt x .g\left( x \right)$$, then $$g\left( x \right)$$ equals
$${\tan ^{ - 1}}\left( {{{6x\sqrt x } \over {1 - 9{x^3}}}} \right)$$ is $$\sqrt x .g\left( x \right)$$, then $$g\left( x \right)$$ equals
19
$$\mathop {\lim }\limits_{x \to {\pi \over 2}} {{\cot x - \cos x} \over {{{\left( {\pi - 2x} \right)}^3}}}$$ equals
Physics
1
A particle is executing simple harmonic motion with a time period T. At time t = 0, it is at its position of
equilibrium. The kinetic energy – time graph of the particle will look like:
2
A diverging lens with magnitude of focal length 25 cm is placed at a distance of 15cm from a converging
lens of magnitude of focal length 20cm. A beam of parallel light falls on the diverging lens. The final
image formed is:
3
In a Young’s double slit experiment, slits are separated by 0.5 mm, and the screen is placed 150 cm away.
A beam of light consisting of two wavelengths, 650 nm and 520 nm, is used to obtain interference fringes
on the screen. The least distance from the common central maximum to the point where the bright fringes
due to both the wavelengths coincide is
4
In a coil of resistance 100 $$\Omega $$, a current is induced by changing
the magnetic flux through it as shown in the figure. The
magnitude of change in flux through the coil is:


5
When a current of 5 mA is passed through a galvanometer having a coil of resistance 15$$\Omega $$, it shows full
scale deflection. The value of the resistance to be put in series with the galvanometer to convert it into a
voltmeter of range 0 – 10V is:
6
A magnetic needle of magnetic moment 6.7 $$\times$$ 10-2 A m2 and moment of inertia 7.5 $$\times$$ 10-6 kg m2 is
performing simple harmonic oscillations in a magnetic field of 0.01 T. Time taken for 10 complete oscillations is:
7

In the given circuit, the current in each resistance is:
8
Which of the following statements is false?
9
In the given circuit diagram when the current reaches steady state in the
circuit, the charge on the capacitor of capacitance C will be:


10
An electric dipole has a fixed dipole moment $$\overrightarrow p $$, which makes angle $$\theta$$ with respect to x-axis. When
subjected to an electric field $$\mathop {{E_1}}\limits^ \to = E\widehat i$$ , it experiences a torque $$\overrightarrow {{T_1}} = \tau \widehat k$$ . When subjected to another electric
field $$\mathop {{E_2}}\limits^ \to = \sqrt 3 {E_1}\widehat j$$ it experiences a torque $$\mathop {{T_2}}\limits^ \to = \mathop { - {T_1}}\limits^ \to $$ . The angle $$\theta$$ is:
11
A capacitance of 2 $$\mu $$F is required in an electrical circuit across a potential difference of 1.0 kV. A large
number of 1 $$\mu $$F capacitors are available which can withstand a potential difference of not more than 300 V.
The minimum number of capacitors required to achieve this is:
12
An electron beam is accelerated by a potential difference V to hit a metallic target to produce X–rays. It
produces continuous as well as characteristic X-rays. If $$\lambda $$min is the smallest possible wavelength of X-ray in the spectrum, the variation of log$$\lambda $$min with log V is correctly represented in:
13
CP and Cv are specific heats at constant pressure and constant volume respectively. It is observed that
CP – Cv = a for hydrogen gas
CP – Cv = b for nitrogen gas
The correct relation between a and b is
CP – Cv = a for hydrogen gas
CP – Cv = b for nitrogen gas
The correct relation between a and b is
14
The temperature of an open room of volume 30 m3 increases from 17oC to 27oC due to the sunshine. The atmospheric pressure in the room remains 1 $$ \times $$ 105 Pa. If Ni
and Nf are the number of molecules in the room
before and after heating, then Nf – Ni will be :
15
An external pressure P is applied on a cube at 0oC so that it is equally compressed from all sides. K is the
bulk modulus of the material of the cube and $$\alpha$$ is its coefficient of linear expansion. Suppose we want to
bring the cube to its original size by heating. The temperature should be raised by:
16
The variation of acceleration due to gravity $$g$$ with distance d from centre of the earth is best represented by
(R = Earth’s radius):
17
A copper ball of mass 100 gm is at a temperature T. It is dropped in a copper calorimeter of mass 100 gm,
filled with 170 gm of water at room temperature. Subsequently, the temperature of the system is found to
be 75oC. T is given by: (Given : room temperature = 30oC, specific heat of copper = 0.1 cal/gmoC)
18
A man grows into a giant such that his linear dimensions increase by a factor of 9. Assuming that his
density remains same, the stress in the leg will change by a factor of :
19
A slender uniform rod of mass M and length $$l$$ is pivoted at one end so that it
can rotate in a vertical plane (see figure). There is negligible friction at the
pivot. The free end is held vertically above the pivot and then released. The
angular acceleration of the rod when it makes an angle $$\theta$$ with the vertical is


20
The moment of inertia of a uniform cylinder of length $$l$$ and radius R about its perpendicular bisector is $$I$$.
What is the ratio $${l \over R}$$ such that the moment of inertia is minimum?
21
A body of mass m = 10–2 kg is moving in a medium and experiences a frictional force F = –kv2. Its initial speed is v0 = 10 ms–1. If, after 10 s, its energy is $${1 \over 8}mv_0^2$$, the value of k will be:
22
A time dependent force F = 6t acts on a particle of mass 1 kg. If the particle starts from rest, the work done
by the force during the first 1 sec. will be:
23
A body is thrown vertically upwards. Which one of the following graphs correctly represent the velocity vs
time?
24
The following observations were taken for determining surface tension T of water by capillary method:
diameter of capillary, D = 1.25 $$\times$$ 10-2 m
rise of water, h = 1.45 $$\times$$ 10-2m
Using g = 9.80 m/s2 and the simplified relation T = $${{rhg} \over 2} \times {10^3}N/m$$, the possible error in surface tension is closest to :
diameter of capillary, D = 1.25 $$\times$$ 10-2 m
rise of water, h = 1.45 $$\times$$ 10-2m
Using g = 9.80 m/s2 and the simplified relation T = $${{rhg} \over 2} \times {10^3}N/m$$, the possible error in surface tension is closest to :
25
Some energy levels of a molecule are shown in the figure. The
ratio of the wavelengths r = $${{\lambda _1}}$$/$${{\lambda _2}}$$, is given by:
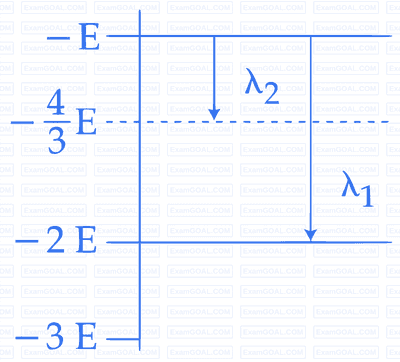

26
A particle A of mass m and initial velocity v collides with a particle B of mass m/2 which is at rest. The
collision is head on, and elastic. The ratio of the de-Broglie wavelengths $${\lambda _A}$$ to $${\lambda _B}$$ after the collision is: