The vapour pressure of acetone at 20^oC is 185 torr. When 1.2 g of a non-volatile substance was dissolved in 100 g of acetone at 20^oC, its vapour pressure was 183 torr. The molar mass (g mol^-1) of the substance is:

In Carius method of estimation of halogens, 250 mg of an organic compound gave 141 mg of AgBr. The percentage of bromine in the compound is: (at. Mass Ag = 108; Br = 80)

The molecular formula of a commercial resin used for exchanging ions in water softening is C₈H₇SO₃Na (Mol. Wt. 206). What would be the maximum uptake of Ca²⁺ ions by the resin when expressed in mole per gram resin?

The following reaction is performed at 298 K
2NO(g) + O₂ (g) $$\leftrightharpoons$$ 2NO₂ (g)
The standard free energy of formation of NO(g) is 86.6 kJ/mol at 298 K. What is the standard free energy of formation of NO₂(g) at 298 K? (KP = 1.6 × 10¹²)

The standard Gibbs energy change at 300 K for the reaction 2A $$\leftrightharpoons$$ B + C is 2494.2 J. At a given time, the composition of the reaction mixture is [A] = 1/2, [B] = 2 and [C] = 1/2. The reaction proceeds in the: [R = 8.314 J/K/mol, e = 2.718]

Two Faraday of electricity is passed through a solution of CuSO₄. The mass of copper deposited at the cathode is: (at. mass of Cu = 63.5 amu)

The intermolecular interaction that is dependent on the inverse cube of distance between the molecule is:

Which of the vitamins given below is water soluble?

Match the catalysts to the correct processes :

	Catalyst		Process
(A)	TiCl3	(i)	Wacker process
(B)	PdCl2	(ii)	Ziegler - Natta polymerization
(C)	CuCl2	(iii)	Contact process
(D)	V2O5	(iv)	Deacon's process

In the reaction


The product $$E$$ is :

Which compound would give $$5$$ - keto - $$2$$ - methylhexanal upon ozonolysis?

In the following sequence of reactions:


The product C is

The synthesis of alkyl fluorides is best accomplished by:

The number of geometric isomers that can exist for square planar [Pt (Cl) (py) (NH₃) (NH₂OH)]+ is (py = pyridine) :

The colour of KMnO₄ is due to :

Which of the following compounds is not colored yellow?

Assertion : Nitrogen and Oxygen are the main components in the atmosphere but these do not react to form oxides of nitrogen.

Reason : The reaction between nitrogen and oxygen requires high temperature.

Which one has the highest boiling point?

Higher order (>3) reactions are rare due to

The ionic radii (in Å) of N^3–, O^2– and F^– are respectively:

Which of the following is the energy of a possible excited state of hydrogen?

If the function.

$$g\left( x \right) = \left\{ {\matrix{ {k\sqrt {x + 1} ,} & {0 \le x \le 3} \cr {m\,x + 2,} & {3 < x \le 5} \cr } } \right.$$

is differentiable, then the value of $$k+m$$ is :

The mean of the data set comprising of 16 observations is 16. If one of the observation valued 16 is deleted and three new observations valued 3, 4 and 5 are added to the data, then the mean of the resultant data, is :

$$\mathop {\lim }\limits_{x \to 0} {{\left( {1 - \cos 2x} \right)\left( {3 + \cos x} \right)} \over {x\tan 4x}}$$ is equal to

Let $$\alpha $$ and $$\beta $$ be the roots of equation $${x^2} - 6x - 2 = 0$$. If $${a_n} = {\alpha ^n} - {\beta ^n},$$ for $$n \ge 1,$$ then the value of $${{{a_{10}} - 2{a_8}} \over {2{a_9}}}$$ is equal to :

If $$12$$ different balls are to be placed in $$3$$ identical boxes, then the probability that one of the boxes contains exactly $$3$$ balls is :

Let $$y(x)$$ be the solution of the differential equation

$$\left( {x\,\log x} \right){{dy} \over {dx}} + y = 2x\,\log x,\left( {x \ge 1} \right).$$ Then $$y(e)$$ is equal to :

The area (in sq. units) of the region described by

$$\left\{ {\left( {x,y} \right):{y^2} \le 2x} \right.$$ and $$\left. {y \ge 4x - 1} \right\}$$ is :

The integral
$$\int\limits_2^4 {{{\log \,{x^2}} \over {\log {x^2} + \log \left( {36 - 12x + {x^2}} \right)}}dx} $$ is equal to :

The integral $$\int {{{dx} \over {{x^2}{{\left( {{x^4} + 1} \right)}^{3/4}}}}} $$ equals :

If $$A = \left[ {\matrix{ 1 & 2 & 2 \cr 2 & 1 & { - 2} \cr a & 2 & b \cr } } \right]$$ is a matrix satisfying the equation

$$A{A^T} = 9\text{I},$$ where $$I$$ is $$3 \times 3$$ identity matrix, then the ordered

pair $$(a, b)$$ is equal to :

The set of all values of $$\lambda $$ for which the system of linear equations:

$$\matrix{ {2{x_1} - 2{x_2} + {x_3} = \lambda {x_1}} \cr {2{x_1} - 3{x_2} + 2{x_3} = \lambda {x_2}} \cr { - {x_1} + 2{x_2} = \lambda {x_3}} \cr } $$

has a non-trivial solution

Let $$f(x)$$ be a polynomial of degree four having extreme values
at $$x=1$$ and $$x=2$$. If $$\mathop {\lim }\limits_{x \to 0} \left[ {1 + {{f\left( x \right)} \over {{x^2}}}} \right] = 3$$, then f$$(2)$$ is equal to :

Let $${\tan ^{ - 1}}y = {\tan ^{ - 1}}x + {\tan ^{ - 1}}\left( {{{2x} \over {1 - {x^2}}}} \right),$$
where $$\left| x \right| < {1 \over {\sqrt 3 }}.$$ Then a value of $$y$$ is :

Let $$O$$ be the vertex and $$Q$$ be any point on the parabola, $${{x^2} = 8y}$$. If the point $$P$$ divides the line segment $$OQ$$ internally in the ratio $$1:3$$, then locus of $$P$$ is :

Locus of the image of the point $$(2, 3)$$ in the line $$\left( {2x - 3y + 4} \right) + k\left( {x - 2y + 3} \right) = 0,\,k \in R,$$ is a :

The number of points, having both co-ordinates as integers, that lie in the interior of the triangle with vertices $$(0, 0)$$ $$(0, 41)$$ and $$(41, 0)$$ is :

If m is the A.M. of two distinct real numbers l and n $$(l,n > 1)$$ and $${G_1},{G_2}$$ and $${G_3}$$ are three geometric means between $$l$$ and n, then $$G_1^4\, + 2G_2^4\, + G_3^4$$ equals:

The number of integers greater than 6,000 that can be formed, using the digits 3, 5, 6, 7 and 8, without repetition, is:

A complex number z is said to be unimodular if $$\,\left| z \right| = 1$$. Suppose $${z_1}$$ and $${z_2}$$ are complex numbers such that $${{{z_1} - 2{z_2}} \over {2 - {z_1}\overline {{z_2}} }}$$ is unimodular and $${z_2}$$ is not unimodular. Then the point $${z_1}$$ lies on a :

Let A and B be two sets containing four and two elements respectively. Then, the number of subsets of the set A $\times$ B , each having atleast three elements are

As an electron makes a transition from an excited state to the ground state of a hydrogen - like atom/ion :

A red $$LED$$ emits light at $$0.1$$ watt uniformly around it. The amplitude of the electric field of the light at a distance of $$1$$ $$m$$ from the diode is :

Monochromatic light is incident on a glass prism of angle $$A$$. If the refractive index of the material of the prism is $$\mu $$, a ray, incident at an angle $$\theta $$. on the face $$AB$$ would get transmitted through the face $$AC$$ of the prism provided :

An inductor $$(L=0.03$$ $$H)$$ and a resistor $$\left( {R = 0.15\,k\Omega } \right)$$ are connected in series to a battery of $$15V$$ $$EMF$$ in a circuit shown below. The key $${K_1}$$ has been kept closed for a long time. Then at $$t=0$$, $${K_1}$$ is opened and key $${K_2}$$ is closed simultaneously. At $$t=1$$ $$ms,$$ the current in the circuit will be : $$\left( {{e^5} \cong 150} \right)$$

An $$LCR$$ circuit is equivalent to a damped pendulum. In an $$LCR$$ circuit the capacitor is charged to $${Q_0}$$ and then connected to the $$L$$ and $$R$$ as shown below :

If a student plots graphs of the square of maximum charge $$\left( {Q_{Max}^2} \right)$$ on the capacitor with time$$(t)$$ for two different values $${L_1}$$ and $${L_2}$$ $$\left( {{L_1} > {L_2}} \right)$$ of $$L$$ then which of the following represents this graph correctly ?
$$\left( {plots\,\,are\,\,schematic\,\,and\,\,niot\,\,drawn\,\,to\,\,scale} \right)$$

Assuming human pupil to have a radius of $$0.25$$ $$cm$$ and a comfortable viewing distance of $$25$$ $$cm$$, the minimum separation between two objects that human eye can resolve at $$500$$ $$nm$$ wavelength is :

On a hot summer night, the refractive index of air is smallest near the ground and increases with height from the ground. When a light beam is directed horizontally, the Huygens' principle leads us to conclude that as it travels, the light beam :

Two coaxial solenoids of different radius carry current $$I$$ in the same direction. $$\overrightarrow {{F_1}} $$ be the magnetic force on the inner solenoid due to the outer one and $$\overrightarrow {{F_2}} $$ be the magnetic force on the outer solenoid due to the inner one. Then :

A rectangular loop of sides $$10$$ $$cm$$ and $$5$$ $$cm$$ carrying a current $$1$$ of $$12A$$ is placed in different orientations as shown in the figures below :

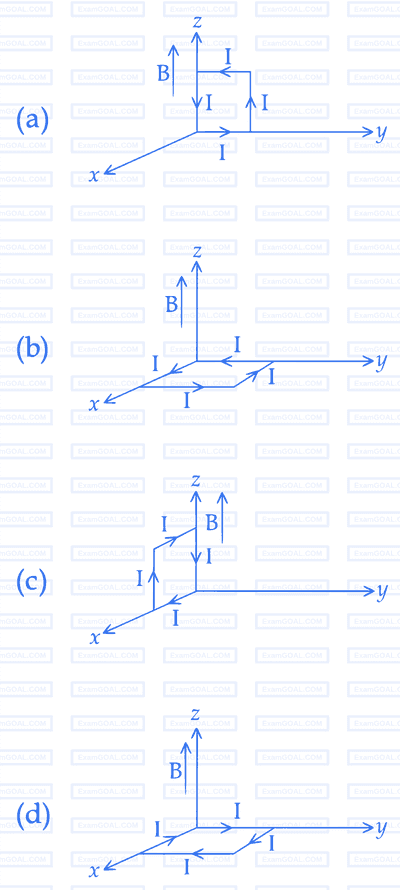
If there is a uniform magnetic field of $$0.3$$ $$T$$ in the positive $$z$$ direction, in which orientations the loop would be in $$(i)$$ stable equilibrium and $$(ii)$$ unstable equilibrium ?

Two stones are thrown up simultaneously from the edge of a cliff $$240$$ $$m$$ high with initial speed of $$10$$ $$m/s$$ and $$40$$ $$m/s$$ respectively. Which of the following graph best represents the time variation of relative position of the second stone with respect to the first ?

(Assume stones do not rebound after hitting the ground and neglect air resistance, take $$g = 10m/{s^2}$$)

(The figures are schematic and not drawn to scale)

In the circuit shown, the current in the $$1\Omega $$ resistor is :

Two long current carrying thin wires, both with current $$I,$$ are held by insulating threads of length $$L$$ and are in equilibrium as shown in the figure, with threads making an angle $$'\theta '$$ with the vertical. If wires have mass $$\lambda $$ per unit-length then the value of $$I$$ is :
($$g=$$ $$gravitational$$ $$acceleration$$ )

When $$5V$$ potential difference is applied across a wire of length $$0.1$$ $$m,$$ the drift speed of electrons is $$2.5 \times {10^{ - 4}}\,\,m{s^{ - 1}}.$$ If the electron density in the wire is $$8 \times {10^{28}}\,\,{m^{ - 3}},$$ the resistivity of the material is close to :

A long cylindrical shell carries positives surfaces change $$\sigma $$ in the upper half and negative surface charge - $$\sigma $$ in the lower half. The electric field lines around the cylinder will look like figure given in :
(figures are schematic and not drawn to scale)

A uniformly charged solid sphere of radius $$R$$ has potential $${V_0}$$ (measured with respect to $$\infty $$) on its surface. For this sphere the equipotential surfaces with potentials $${{3{V_0}} \over 2},\,{{5{V_0}} \over 4},\,{{3{V_0}} \over 4}$$ and $${{{V_0}} \over 4}$$ have radius $${R_1},\,\,{R_2},\,\,{R_3}$$ and $${R_4}$$ respectively. Then

In the given circuit, charges $${Q_2}$$ on the $$2\mu F$$ capacitor changes as $$C$$ is varied from $$1\,\mu F$$ to $$3\mu F.$$ $${Q_2}$$ as a function of $$'C'$$ is given properly by:
$$\left( {figures\,\,are\,\,drawn\,\,schematically\,\,and\,\,are\,\,not\,\,to\,\,scale} \right)$$

For a simple pendulum, a graph is plotted between its kinetic energy $$(KE)$$ and potential energy $$(PE)$$ against its displacement $$d.$$ Which one of the following represents these correctly?
$$(graphs$$ $$are$$ $$schematic$$ $$and$$ $$not$$ $$drawn$$ $$to$$ $$scale)$$

A pendulum made of a uniform wire of cross sectional area $$A$$ has time period $$T.$$ When an additional mass $$M$$ is added to its bob, the time period changes to $${T_{M.}}$$ If the Young's modulus of the material of the wire is $$Y$$ then $${1 \over Y}$$ is equal to :
($$g=$$ $$gravitational$$ $$acceleration$$)

From a solid sphere of mass $$M$$ and radius $$R,$$ a spherical portion of radius $$R/2$$ is removed, as shown in the figure. Taking gravitational potential $$V=0$$ at $$r = \infty ,$$ the potential at the center of the cavity thus formed is:
($$G=gravitational $$ $$constant$$)

Consider a spherical shell of radius $$R$$ at temperature $$T$$. The black body radiation inside it can be considered as an ideal gas of photons with internal energy per unit volume $$u = {U \over V}\, \propto \,{T^4}$$ and pressure $$p = {1 \over 3}\left( {{U \over V}} \right)$$ . If the shell now undergoes an adiabatic expansion the relation between $$T$$ and $$R$$ is:

Consider an ideal gas confined in an isolated closed chamber. As the gas undergoes an adiabatic expansion, the average time of collision between molecules increases as $${V^q},$$ where $$V$$ is the volume of the gas. The value of $$q$$ is: $$\left( {\gamma = {{{C_p}} \over {{C_v}}}} \right)$$

A solid body of constant heat capacity $$1$$ $$J/{}^ \circ C$$ is being heated by keeping it in contact with reservoirs in two ways:
$$(i)$$ Sequentially keeping in contact with $$2$$ reservoirs such that each reservoir
$$\,\,\,\,\,\,\,\,$$supplies same amount of heat.
$$(ii)$$ Sequentially keeping in contact with $$8$$ reservoirs such that each reservoir
$$\,\,\,\,\,\,\,\,\,\,$$supplies same amount of heat.
In both the cases body is brought from initial temperature $${100^ \circ }C$$ to final temperature $${200^ \circ }C$$. Entropy change of the body in the two cases respectively is :

Given in the figure are two blocks $$A$$ and $$B$$ of weight 20 N and 100 N, respectively. These are being pressed against a wall by a force $$F$$ as shown. If the coefficient of friction between the blocks is 0.1 and between block $$B$$ and the wall is 0.15, the frictional force applied by the wall on block $$B$$ is :

From a solid sphere of mass $$M$$ and radius $$R$$ a cube of maximum possible volume is cut. Moment of inertia of cube about an axis passing through its center and perpendicular to one of its face is:

Distance of the center of mass of a solid uniform cone from its vertex is $$z{}_0$$. If the radius of its base is $$R$$ and its height is $$h$$ then $$z{}_0$$ is equal to :

A particle of mass $$m$$ moving in the $$x$$ direction with speed $$2v$$ is hit by another particle of mass $$2m$$ moving in the $$y$$ direction with speed $$v.$$ If the collision is perfectly inelastic, the percentage loss in the energy during the collision is close to:

The period of oscillation of a simple pendulum is $$T = 2\pi \sqrt {{L \over g}} $$. Measured value of L is 20.0 cm known to 1 mm accuracy and time for 100 oscillations of the pendulum is found to be 90 s using wrist watch of 1 s resolution. The accuracy in the determination of g is: