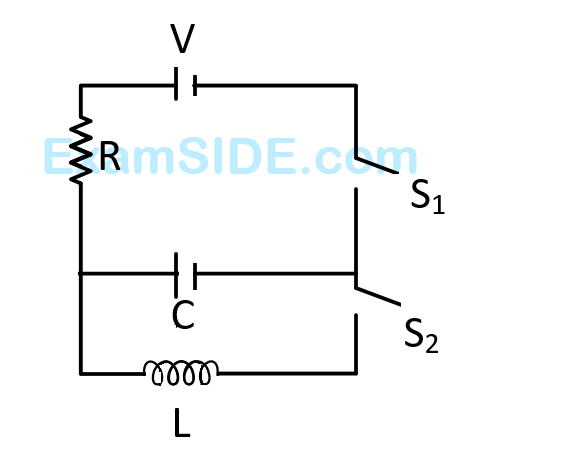
1
Let A and B be two sets containing 2 elements and
4 elements respectively. The number of subsets of
A $$ \times $$ B having 3 or more elements is :
2
All the students of a class performed poorly in Mathematics. The teacher decided to give grace marks of 10
to each of the students. Which of the following statistical measures will not change even after the grace
marks were given?
3
$$\mathop {\lim }\limits_{x \to 0} {{\left( {1 - \cos 2x} \right)\left( {3 + \cos x} \right)} \over {x\tan 4x}}$$ is equal to
4
At present, a firm is manufacturing $$2000$$ items. It is estimated that the rate of change of production P w.r.t. additional number of workers $$x$$ is given by $${{dp} \over {dx}} = 100 - 12\sqrt x .$$ If the firm employs $$25$$ more workers, then the new level of production of items is
5
The area (in square units) bounded by the curves $$y = \sqrt {x,} $$ $$2y - x + 3 = 0,$$ $$x$$-axis, and lying in the first quadrant is :
6
Statement-1 : The value of the integral
$$\int\limits_{\pi /6}^{\pi /3} {{{dx} \over {1 + \sqrt {\tan \,x} }}} $$ is equal to $$\pi /6$$
Statement-2 : $$\int\limits_a^b {f\left( x \right)} dx = \int\limits_a^b {f\left( {a + b - x} \right)} dx.$$
7
If $$\int {f\left( x \right)dx = \psi \left( x \right),} $$ then $$\int {{x^5}f\left( {{x^3}} \right)dx} $$ is equal to
8
If $$x, y, z$$ are in A.P. and $${\tan ^{ - 1}}x,{\tan ^{ - 1}}y$$ and $${\tan ^{ - 1}}z$$ are also in A.P., then :
9
If $$y = \sec \left( {{{\tan }^{ - 1}}x} \right),$$ then $${{{dy} \over {dx}}}$$ at $$x=1$$ is equal to :
10
The equation of the circle passing through the foci of the ellipse $${{{x^2}} \over {16}} + {{{y^2}} \over 9} = 1$$, and having centre at $$(0,3)$$ is :
11
The $$x$$-coordinate of the incentre of the triangle that has the coordinates of mid points of its sides as $$(0, 1) (1, 1)$$ and $$(1, 0)$$ is :
12
A ray of light along $$x + \sqrt 3 y = \sqrt 3 $$ gets reflected upon reaching $$X$$-axis, the equation of the reflected ray is :
13
The term independent of $$x$$ in expansion of
$${\left( {{{x + 1} \over {{x^{2/3}} - {x^{1/3}} + 1}} - {{x - 1} \over {x - {x^{1/2}}}}} \right)^{10}}$$ is
14
Let $${T_n}$$ be the number of all possible triangles formed by joining vertices of an n-sided regular polygon. If $${T_{n + 1}} - {T_n}$$ = 10, then the value of n is :
15
If the equations $${x^2} + 2x + 3 = 0$$ and $$a{x^2} + bx + c = 0,$$ $$a,\,b,\,c\, \in \,R,$$ have a common root, then $$a\,:b\,:c\,$$ is
16
The number of values of $$k$$, for which the system of equations : $$$\matrix{
{\left( {k + 1} \right)x + 8y = 4k} \cr
{kx + \left( {k + 3} \right)y = 3k - 1} \cr
} $$$
has no solution, is
17
The real number $$k$$ for which the equation, $$2{x^3} + 3x + k = 0$$ has two distinct real roots in $$\left[ {0,\,1} \right]$$
18
If z is a complex number of unit modulus and argument $$\theta $$, then arg $$\left( {{{1 + z} \over {1 + \overline z }}} \right)$$ equals :
19
The expression $${{\tan {\rm A}} \over {1 - \cot {\rm A}}} + {{\cot {\rm A}} \over {1 - \tan {\rm A}}}$$ can be written as:
20
If the vectors $$\overrightarrow {AB} = 3\widehat i + 4\widehat k$$ and $$\overrightarrow {AC} = 5\widehat i - 2\widehat j + 4\widehat k$$ are the sides of a triangle $$ABC,$$ then the length of the median through $$A$$ is :
21
If the lines $${{x - 2} \over 1} = {{y - 3} \over 1} = {{z - 4} \over { - k}}$$ and $${{x - 1} \over k} = {{y - 4} \over 2} = {{z - 5} \over 1}$$ are coplanar, then $$k$$ can have :