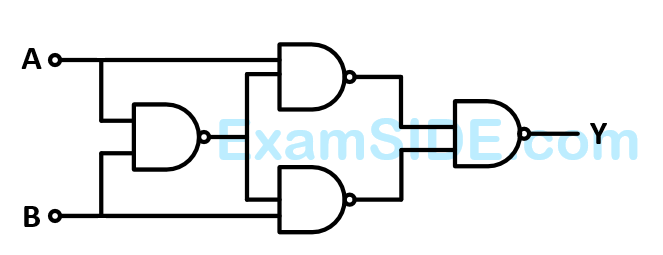
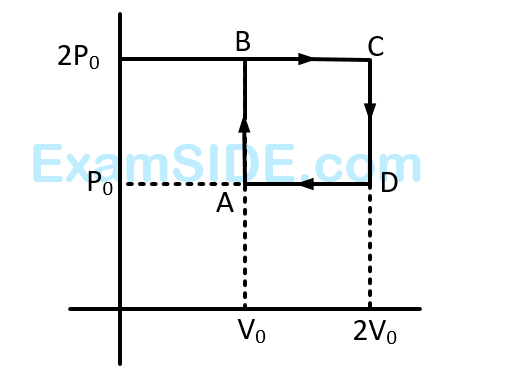
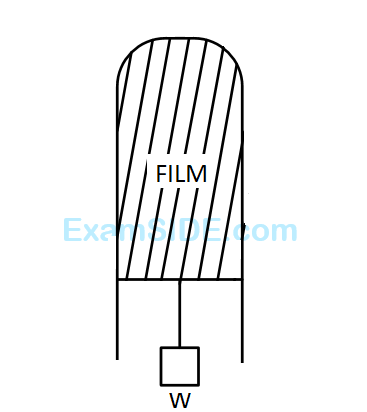
1
Let X = {1, 2, 3, 4, 5}. The number of different ordered pairs (Y, Z) that can be formed such that Y $$ \subseteq $$ X, Z $$ \subseteq $$ X and Y $$ \cap $$ Z is empty, is :
2
Let x1, x2,........., xn be n observations, and let $$\overline x $$ be their arithematic mean and $${\sigma ^2}$$ be their variance.
Statement 1 : Variance of 2x1, 2x2,......., 2xn is 4$${\sigma ^2}$$.
Statement 2 : : Arithmetic mean of 2x1, 2x2,......, 2xn is 4$$\overline x $$.
3
If $$f:R \to R$$ is a function defined by
$$f\left( x \right) = \left[ x \right]\cos \left( {{{2x - 1} \over 2}} \right)\pi $$,
where [x] denotes the greatest integer function, then $$f$$ is
4
Consider the function, $$f\left( x \right) = \left| {x - 2} \right| + \left| {x - 5} \right|,x \in R$$
Statement - 1 : $$f'\left( 4 \right) = 0$$
Statement - 2 : $$f$$ is continuous in [2, 5], differentiable in (2, 5) and $$f$$(2) = $$f$$(5)
5
Let $$a,b \in R$$ be such that the function $$f$$ given by $$f\left( x \right) = In\left| x \right| + b{x^2} + ax,\,x \ne 0$$ has extreme values at $$x=-1$$ and $$x=2$$
Statement-1 : $$f$$ has local maximum at $$x=-1$$ and at $$x=2$$.
Statement-2 : $$a = {1 \over 2}$$ and $$b = {-1 \over 4}$$
6
Let $$\overrightarrow a $$ and $$\overrightarrow b $$ be two unit vectors. If the vectors $$\,\overrightarrow c = \widehat a + 2\widehat b$$ and $$\overrightarrow d = 5\widehat a - 4\widehat b$$ are perpendicular to each other, then the angle between $$\overrightarrow a $$ and $$\overrightarrow b $$ is :
7
Three numbers are chosen at random without replacement from $$\left\{ {1,2,3,..8} \right\}.$$ The probability that their minimum is $$3,$$ given that their maximum is $$6,$$ is :
8
The population $$p$$ $$(t)$$ at time $$t$$ of a certain mouse species satisfies the differential equation $${{dp\left( t \right)} \over {dt}} = 0.5\,p\left( t \right) - 450.\,\,$$ If $$p(0)=850,$$ then the time at which the population becomes zero is :
9
If $$g\left( x \right) = \int\limits_0^x {\cos 4t\,dt,} $$ then $$g\left( {x + \pi } \right)$$ equals
10
The area between the parabolas $${x^2} = {y \over 4}$$ and $${x^2} = 9y$$ and the straight line $$y=2$$ is :
11
If the $$\int {{{5\tan x} \over {\tan x - 2}}dx = x + a\,\ln \,\left| {\sin x - 2\cos x} \right| + k,} $$ then $$a$$ is
equal to :
12
A line is drawn through the point $$(1, 2)$$ to meet the coordinate axes at $$P$$ and $$Q$$ such that it forms a triangle $$OPQ,$$ where $$O$$ is the origin. If the area of the triangle $$OPQ$$ is least, then the slope of the line $$PQ$$ is :
13
If the line $${{x - 1} \over 2} = {{y + 1} \over 3} = {{z - 1} \over 4}$$ and $${{x - 3} \over 1} = {{y - k} \over 2} = {z \over 1}$$ intersect, then $$k$$ is equal to :
14
A spherical balloon is filled with $$4500\pi $$ cubic meters of helium gas. If a leak in the balloon causes the gas to escape at the rate of $$72\pi $$ cubic meters per minute, then the rate (in meters per minute) at which the radius of the balloon decreases $$49$$ minutes after the leakage began is :
15
An ellipse is drawn by taking a diameter of thec circle $${\left( {x - 1} \right)^2} + {y^2} = 1$$ as its semi-minor axis and a diameter of the circle $${x^2} + {\left( {y - 2} \right)^2} = 4$$ is semi-major axis. If the centre of the ellipse is at the origin and its axes are the coordinate axes, then the equation of the ellipse is :
16
The length of the diameter of the circle which touches the $$x$$-axis at the point $$(1, 0)$$ and passes through the point $$(2, 3)$$ is :
17
If the line $$2x + y = k$$ passes through the point which divides the line segment joining the points $$(1, 1)$$ and $$(2, 4)$$ in the ratio $$3 : 2$$, then $$k$$ equals :
18
If $$n$$ is a positive integer, then $${\left( {\sqrt 3 + 1} \right)^{2n}} - {\left( {\sqrt 3 - 1} \right)^{2n}}$$ is :
19
Assuming the balls to be identical except for difference in colours, the number of ways in which one or more balls can be selected from 10 white, 9 green and 7 black balls is:
20
The equation $${e^{\sin x}} - {e^{ - \sin x}} - 4 = 0$$ has:
21
If $$z \ne 1$$ and $$\,{{{z^2}} \over {z - 1}}\,$$ is real, then the point represented by the complex number z lies :
22
Let $$ABCD$$ be a parallelogram such that $$\overrightarrow {AB} = \overrightarrow q ,\overrightarrow {AD} = \overrightarrow p $$ and $$\angle BAD$$ be an acute angle. If $$\overrightarrow r $$ is the vector that coincide with the altitude directed from the vertex $$B$$ to the side $$AD,$$ then $$\overrightarrow r $$ is given by :