In the following sequence of reactions, the alkene affords the compound ‘B’
CH₃ - CH = CH - CH₃ $$\buildrel {{O_3}} \over \longrightarrow $$ A $$\mathrel{\mathop{\kern0pt\longrightarrow} \limits_{Zn}^{H{}_2O}} $$ B
The compound B is

Toluene is nitrated and the resulting product is reduced with tin and hydrochloric acid. The product so obtained is diazotised and then heated with cuprous bromide. The reaction mixture so formed contains

The hydrocarbon which can react with sodium in liquid ammonia is

The correct decreasing order of priority for the functional groups of organic compounds in the IUPAC system of nomenclature is

For the following three reactions a, b and c, equilibrium constants are given:
a. CO (g) + H₂O (g) $$\leftrightharpoons$$ CO₂(g) + H₂ (g) ; K₁
b. CH₄ (g) + H₂O (g) $$\leftrightharpoons$$ CO(g) + 3H₂ (g) ; K₂
c. CH₄ (g) + 2H₂O (g) $$\leftrightharpoons$$ CO₂(g) + 4H₂ (g) ; K₃

The pK_a of a weak acid, HA, is 4.80. The pK_b of a weak base, BOH, is 4.78. The pH of an aqueous solution of the corresponding salt, BA, will be

Four species are listed below
i. $$HCO_3^−$$
ii. $$H_3O^+$$
iii. $$HSO_4^−$$
iv. $$HSO_3F$$
Which one of the following is the correct sequence of their acid strength?

The equilibrium constants K_P1 and K_P2 for the reactions X $$\leftrightharpoons$$ 2Y and Z $$\leftrightharpoons$$ P + Q, respectively are in the ratio of 1 : 9. If the degree of dissociation of X and Z be equal then the ratio of total pressure at these equilibria is :

Standard entropy of X₂, Y₂ and XY₃ are 60, 40 and 50 JK⁻¹ mol⁻¹ , respectively. For the reaction,
$${1 \over 2} X_2$$ + $${3 \over 2} Y_2 \to$$ XY₃, $$\Delta H$$ = -30 kJ, to be at equilibrium, the temperature will be :

Oxidising power of chlorine in aqueous solution can be determined by the parameters indicated below:
$${1 \over 2}C{l_2}(g)$$ $$\buildrel {{1 \over 2}{\Delta _{diss}}{H^\Theta }} \over \longrightarrow $$ $$Cl(g)$$ $$\buildrel {{\Delta _{eg}}{H^\Theta }} \over \longrightarrow $$ $$C{l^ - }(g)$$ $$\buildrel {{\Delta _{Hyd}}{H^\Theta }} \over \longrightarrow $$ $$C{l^ - }(aq)$$
(Using the data, $${\Delta _{diss}}H_{C{l_2}}^\Theta $$ = 240 kJ/mol, $${\Delta _{eg}}H_{Cl}^\Theta $$ = -349 kJ/mol, $${\Delta _{hyd}}H_{C{l^ - }}^\Theta $$ = - 381 kJ/mol) will be :

Amount of oxalic acid present in a solution can be determined by its titration with $$KMn{O_4}$$ solution in the presence of $${H_2}S{O_4}.$$ The titration gives unsatisfactory result when carried out in the presence of $$HCl,$$ because $$HCl$$ :

The treatment of $$C{H_3}MgX\,\,$$ with $$C{H_3}C \equiv C - H$$ produces

The absolute configuration of

The electrophile, $${E^ \oplus }$$ attacks the benzene ring to generate the intermediate $$\sigma - $$complex. Of the following, which $$\sigma - $$complex is lowest energy?

$$\alpha$$-D-(+)-glucose and $$\beta$$-D-(+)-glucose are

Phenol, when it first reacts with concentrated sulphuric acid and then with concentrated nitric acid, gives

The organic chloro compound, which shows complete stereochemical inversion during a S_N2 reaction, is

The coordination number and the oxidation state of the element ‘E’ in the complex [E(en)₂(C₂O₄)]NO₂ (where (en) is ethylene diamine) are, respectively,

In which of the following octahedral complexes of Co (at. no. 27), will the magnitude of $$\Delta _o$$ be the highest?

Larger number of oxidation states are exhibited by the actinoids than those by the lanthanoids, the main reason being :

Which one of the following is the correct statement?

For a reaction $${1 \over 2}A \to 2B$$ rate of disappearance of ‘A’ is related to the rate of appearance of ‘B’ by the expression

Given $$E_{C{r^{3 + }}/Cr}^o$$ = -0.72 V; $$E_{Fe^{2+}/Fe}^o$$ = -0.42V, The potential for the cell Cr | Cr³⁺ (0.1M) || Fe²⁺ (0.01 M) | Fe is

The vapour pressure of water at 20^oC is 17.5 mm Hg. If 18 g of glucose (C₆H₁₂O₆) is added to 178.2 g of water at 20^oC, the vapour pressure of the resulting solution will be

At 80^oC, the vapour pressure of pure liquid ‘A’ is 520 mm Hg and that of pure liquid ‘B’ is 1000 mm Hg. If a mixture solution of ‘A’ and ‘B’ boils at 80^oC and 1 atm pressure, the amount of ‘A’ in the mixture is (1 atm = 760 mm Hg)

Which of the following pair of species have the same bond order?

The bond dissociation energy of B - F in BF₃ is 646 kJ mol^-1 whereas that of C - F in CF₄ is 515 kj mol^-1. The correct reason for higher B - F bond dissociation energy as compared to that of C - F is

The ionization enthalpy of hydrogen atom is 1.312 × 10⁶ J mol⁻¹. The energy required to excite the electron in the atom from n = 1 to n = 2 is

Which one of the following constitutes a group of the isoelectronic species?

Let $$f\left( x \right) = \left\{ {\matrix{ {\left( {x - 1} \right)\sin {1 \over {x - 1}}} & {if\,x \ne 1} \cr 0 & {if\,x = 1} \cr } } \right.$$

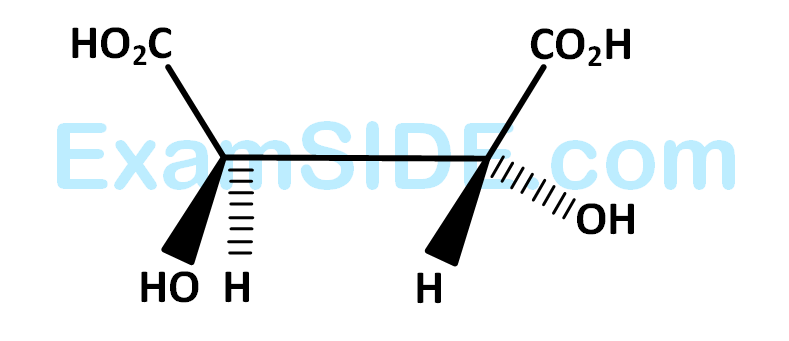
Then which one of the following is true?

Let $$f:N \to Y$$ be a function defined as f(x) = 4x + 3 where
Y = { y $$ \in $$ N, y = 4x + 3 for some x $$ \in $$ N }.
Show that f is invertible and its inverse is

A die is thrown. Let $$A$$ be the event that the number obtained is greater than $$3.$$ Let $$B$$ be the event that the number obtained is less than $$5.$$ Then $$P\left( {A \cup B} \right)$$ is :

It is given that the events $$A$$ and $$B$$ are such that
$$P\left( A \right) = {1 \over 4},P\left( {A|B} \right) = {1 \over 2}$$ and $$P\left( {B|A} \right) = {2 \over 3}.$$ Then $$P(B)$$ is :

The solution of the differential equation

$${{dy} \over {dx}} = {{x + y} \over x}$$ satisfying the condition $$y(1)=1$$ is :

The area of the plane region bounded by the curves $$x + 2{y^2} = 0$$ and $$\,x + 3{y^2} = 1$$ is equal to :

The value of $$\sqrt 2 \int {{{\sin xdx} \over {\sin \left( {x - {\pi \over 4}} \right)}}} $$ is

Let $$a, b, c$$ be any real numbers. Suppose that there are real numbers $$x, y, z$$ not all zero such that $$x=cy+bz,$$ $$y=az+cx,$$ and $$z=bx+ay.$$ Then $${a^2} + {b^2} + {c^2} + 2abc$$ is equal to :

Let $$A$$ be $$a\,2 \times 2$$ matrix with real entries. Let $$I$$ be the $$2 \times 2$$ identity matrix. Denote by tr$$(A)$$, the sum of diagonal entries of $$a$$. Assume that $${a^2} = I.$$
Statement-1 : If $$A \ne I$$ and $$A \ne - I$$, then det$$(A)=-1$$
Statement- 2 : If $$A \ne I$$ and $$A \ne - I$$, then tr $$(A)$$ $$ \ne 0$$.

Suppose the cubic $${x^3} - px + q$$ has three distinct real roots
where $$p>0$$ and $$q>0$$. Then which one of the following holds?

How many real solutions does the equation
$${x^7} + 14{x^5} + 16{x^3} + 30x - 560 = 0$$ have?

The value of $$cot\left( {\cos e{c^{ - 1}}{5 \over 3} + {{\tan }^{ - 1}}{2 \over 3}} \right)$$ is :

The non-zero vectors are $${\overrightarrow a ,\overrightarrow b }$$ and $${\overrightarrow c }$$ are related by $${\overrightarrow a = 8\overrightarrow b }$$ and $${\overrightarrow c = - 7\overrightarrow b \,\,.}$$ Then the angle between $${\overrightarrow a }$$ and $${\overrightarrow c }$$ is :

A parabola has the origin as its focus and the line $$x=2$$ as the directrix. Then the vertex of the parabola is at :

A focus of an ellipse is at the origin. The directrix is the line $$x=4$$ and the eccentricity is $${{1 \over 2}}$$. Then the length of the semi-major axis is :

The point diametrically opposite to the point $$P(1, 0)$$ on the circle $${x^2} + {y^2} + 2x + 4y - 3 = 0$$ is :

The perpendicular bisector of the line segment joining P(1, 4) and Q(k, 3) has y-intercept -4. Then a possible value of k is :

The first two terms of a geometric progression add up to 12. the sum of the third and the fourth terms is 48. If the terms of the geometric progression are alternately positive and negative, then the first term is

How many different words can be formed by jumbling the letters in the word MISSISSIPPI in which no two S are adjacent?

In a shop there are five types of ice-cream available. A child buys six ice-cream.
Statement - 1: The number of different ways the child can buy the six ice-cream is $${}^{10}{C_5}$$.
Statement - 2: The number of different ways the child can buy the six ice-cream is equal to the number of different ways of arranging 6 A and 4 B's in a row.

The quadratic equations $${x^2} - 6x + a = 0$$ and $${x^2} - cx + 6 = 0$$ have one root in common. The other roots of the first and second equations are integers in the ratio 4 : 3. Then the common root is

STATEMENT - 1 : For every natural number $$n \ge 2,$$ $$${1 \over {\sqrt 1 }} + {1 \over {\sqrt 2 }} + ........ + {1 \over {\sqrt n }} > \sqrt n .$$$

STATEMENT - 2 : For every natural number $$n \ge 2,$$, $$$\sqrt {n\left( {n + 1} \right)} < n + 1.$$$

Let R be the real line. Consider the following subsets of the plane $$R \times R$$ :
$$S = \left\{ {(x,y):y = x + 1\,\,and\,\,0 < x < 2} \right\}$$
$$T = \left\{ {(x,y): x - y\,\,\,is\,\,an\,\,{\mathop{\rm int}} eger\,} \right\}$$,

Which one of the following is true ?

The conjugate of a complex number is $${1 \over {i - 1}}$$ then that complex number is :

If the straight lines $$\,\,\,\,\,$$ $$\,\,\,\,\,$$ $${{x - 1} \over k} = {{y - 2} \over 2} = {{z - 3} \over 3}$$ $$\,\,\,\,\,$$ and$$\,\,\,\,\,$$ $${{x - 2} \over 3} = {{y - 3} \over k} = {{z - 1} \over 2}$$ intersects at a point, then the integer $$k$$ is equal to

The line passing through the points $$(5,1,a)$$ and $$(3, b, 1)$$ crosses the $$yz$$-plane at the point $$\left( {0,{{17} \over 2}, - {{ - 13} \over 2}} \right)$$ . Then

In the circuit below, $$A$$ and $$B$$ represent two inputs and $$C$$ represents the output.

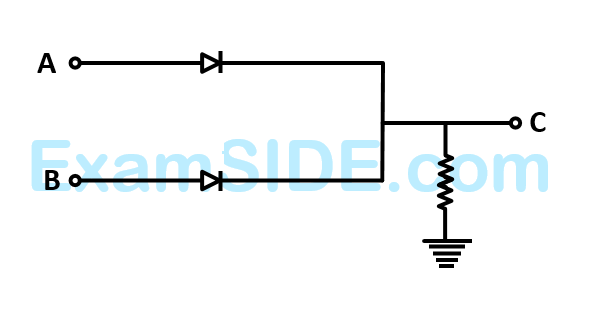
The circuit represents

Suppose an electron is attracted towards the origin by a force $${k \over r}$$ where $$'k'$$ is a constant and $$'r'$$ is the distance of the electron from the origin. By applying Bohr model to this system, the radius of the $${n^{th}}$$ orbital of the electron is found to be $$'{r_n}'$$ and the kinetic energy of the electron to be $$'{T_n}'.$$

Then which of the following is true?

This question contains Statement- 1 and Statement- 2. Of the four choices given after the statements, choose the one that best describes the two statements:
Statement- 1:
Energy is released when heavy nuclei undergo fission or light nuclei undergo fusion and

Statement- 2:
For heavy nuclei, binding energy per nucleon increases with increasing $$Z$$ while for light nuclei it decreases with increasing $$Z.$$

A student measures the focal length of a convex lens by putting an object pin at a distance $$'u'$$ from the lens and measuring the distance $$'v'$$ of the image pin. The graph between $$'u'$$ and $$'v'$$ plotted by the student should look like

In an experiment, electrons are made to pass through a narrow slit of width $$'d'$$ comparable to their de Broglie wavelength. They are detected on a screen at a distance $$'D'$$ from the slit (see figure).

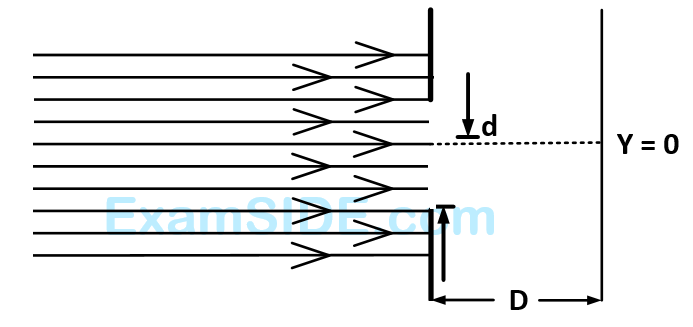
Which of the following graphs can be expected to represent the number of electrons $$'N'$$ detected as a function of the detector position $$'y'\left( {y = 0} \right.$$ corresponds to the middle of the slit$$\left. \, \right)$$

An experiment is performed to find the refractive index of glass using a travelling microscope. In this experiment distances are measured by

Two coaxial solenoids are made by winding thin insulated wire over a pipe of cross-sectional area $$A=$$ $$10\,\,c{m^2}$$ and length $$=20$$ $$cm$$ . If one of the solenoid has $$300$$ turns and the other $$400$$ turns, their mutual inductance is
$$\left( {{\mu _0} = 4\pi \times {{10}^{ - 7}}\,Tm\,{A^{ - 1}}} \right)$$

A horizontal overhead powerline is at height of $$4m$$ from the ground and carries a current of $$100A$$ from east to west. The magnetic field directly below it on the ground is
$$\left( {{\mu _0} = 4\pi \times {{10}^{ - 7}}\,\,Tm\,\,{A^{ - 1}}} \right)$$

Relative permittivity and permeability of a material $${\varepsilon _r}$$ and $${\mu _r},$$ respectively. Which of the following values of these quantities are allowed for a diamagnetic material?

A $$5V$$ battery with internal resistance $$2\Omega $$ and a $$2V$$ battery with internal resistance $$1\Omega $$ are connected to a $$10\Omega $$ resistor as shown in the figure.

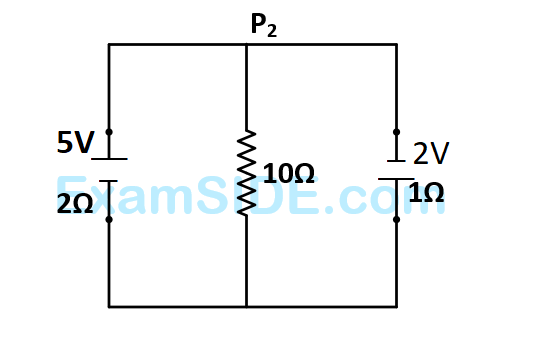
The current in the $$10\Omega $$ resistor is

Consider a block of conducting material of resistivity $$'\rho '$$ shown in the figure. Current $$'I'$$ enters at $$'A'$$ and leaves from $$'D'$$. We apply superposition principle to find voltage $$'\Delta V'$$ developed between $$'B'$$ and $$'C'$$. The calculation is done in the following steps:
(i) Take current $$'I'$$ entering from $$'A'$$ and assume it to spread over a hemispherical surface in the block.
(ii) Calculate field $$E(r)$$ at distance $$'r'$$ from A by using Ohm's law $$E = \rho j,$$ where $$j$$ is the current per unit area at $$'r'$$.
(iii) From the $$'r'$$ dependence of $$E(r)$$, obtain the potential $$V(r)$$ at $$r$$.
(iv) Repeat (i), (ii) and (iii) for current $$'I'$$ leaving $$'D'$$ and superpose results for $$'A'$$ and $$'D'.$$

$$\Delta V$$ measured between $$B$$ and $$C$$ is

A body is at rest at $$x=0.$$ At $$t=0,$$ it starts moving in the positive $$x$$-direction with a constant acceleration. At the same instant another body passes through $$x=0$$ moving in the positive $$x$$ direction with a constant speed. The position of the first body is given by $${x_1}\left( t \right)$$ after time $$'t';$$ and that of the second body by $${x_2}\left( t \right)$$ after the same time interval. Which of the following graphs correctly describes $$\left( {{x_1} - {x_2}} \right)$$ as a function of time $$'t'$$ ?

Consider a block of conducting material of resistivity $$'\rho '$$ shown in the figure. Current $$'I'$$ enters at $$'A'$$ and leaves from $$'D'$$. We apply superposition principle to find voltage $$'\Delta V'$$ developed between $$'B'$$ and $$'C'$$. The calculation is done in the following steps:
(i) Take current $$'I'$$ entering from $$'A'$$ and assume it to spread over a hemispherical surface in the block.
(ii) Calculate field $$E(r)$$ at distance $$'r'$$ from A by using Ohm's law $$E = \rho j,$$ where $$j$$ is the current per unit area at $$'r'$$.
(iii) From the $$'r'$$ dependence of $$E(r)$$, obtain the potential $$V(r)$$ at $$r$$.
(iv) Repeat (i), (ii) and (iii) for current $$'I'$$ leaving $$'D'$$ and superpose results for $$'A'$$ and $$'D'.$$

For current entering at $$A,$$ the electric field at a distance $$'r'$$ from $$A$$ is

A planet in a distant solar system is $$10$$ times more massive than the earth and its radius is $$10$$ times smaller. Given that the escape velocity from the earth is $$11\,\,km\,{s^{ - 1}},$$ the escape velocity from the surface of the planet would be

Shown in the figure below is a meter-bridge set up with null deflection in the galvanometer.

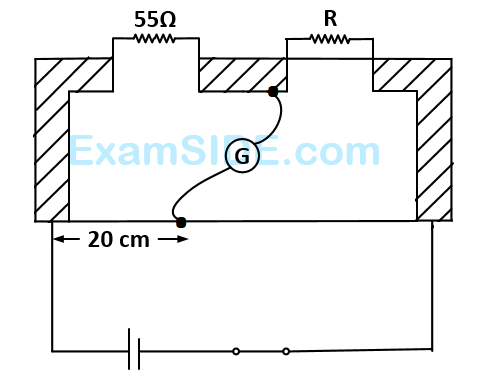
The value of the unknown resister $$R$$ is

A thin spherical shell of radius $$R$$ has charge $$Q$$ spread uniformly over its surface. Which of the following graphs most closely represents the electric field $$E(r)$$ produced by the shell in the range $$0 \le r < \infty ,$$ where $$r$$ is the distance from the center of the shell?

A parallel plate capacitor with air between the plates has capacitance of $$9$$ $$pF.$$ The separation between its plates is $$'d'.$$ The space between the plates has dielectric constant $${k_1}$$ $$=3$$ and thickness $${d \over 3}$$ while the other one has dielectric constant $${k_2} = 6$$ and thickness $${{2d} \over 3}$$. Capacitance of the capacitor is now

A wave travelling along the $$x$$-axis is described by the equation $$y(x, t)=0.005$$ $$\cos \,\left( {\alpha \,x - \beta t} \right).$$ If the wavelength and the time period of the wave are $$0.08$$ $$m$$ and $$2.0s$$, respectively, then $$\alpha $$ and $$\beta $$ in appropriate units are

While measuring the speed of sound by performing a resonance column experiment, a student gets the first resonance condition at a column length of $$18$$ $$cm$$ during winter. Repeating the same experiment during summer, she measures the column length to be $$x$$ $$cm$$ for the second resonance. Then

A jar is filled with two non-mixing liquids $$1$$ and $$2$$ having densities $${\rho _1}$$ and $${\rho _2}$$ respectively. A solid ball, made of a material of density $${\rho _3}$$, is dropped in the jar. It comes to equilibrium in the position shown in the figure. Which of the following is true for $${\rho _1}$$ , $${\rho _1}$$ and $${\rho _3}$$ ?

A capillary tube (A) is dipped in water. Another identical tube (B) is dipped in a soap-water solution. Which of the following shows the relative nature of the liquid columns in the two tubes?

A thin rod of length $$'L'$$ is lying along the $$x$$-axis with its ends at $$x=0$$ and $$x=L$$. Its linear density (mass/length) varies with $$x$$ as $$k{\left( {{x \over L}} \right)^n},$$ where $$n$$ can be zero or any positive number. If the position $${X_{CM}}$$ of the center of mass of the rod is plotted against $$'n',$$ which of the following graphs best approximates the dependence of $${X_{CM}}$$ on $$n$$?

An insulated container of gas has two chambers separated by an insulating partition. One of the chambers has volume $${V_1}$$ and contains ideal gas at pressure $${P_1}$$ and temperature $${T_1}$$. The other chamber has volume $${V_2}$$ and contains ideal gas at pressure $${P_2}$$ and temperature $${T_2}$$. If the partition is removed without doing any work on the gas, the final equilibrium temperature of the gas in the container will be

The speed of sound in oxygen $$\left( {{O_2}} \right)$$ at a certain temperature is $$460\,\,m{s^{ - 1}}.$$ The speed of sound in helium $$(He)$$ at the same temperature will be (assume both gases to be ideal)

A spherical solid ball of volume $$V$$ is made of a material of density $${\rho _1}$$. It is falling through a liquid of density $${\rho _2}\left( {{\rho _2} < {\rho _1}} \right)$$. Assume that the liquid applies a viscous force on the ball that is proportional to the square of its speed $$v,$$ i.e., $${F_{viscous}} = - k{v^2}\left( {k > 0} \right).$$ The terminal speed of the ball is

This question contains Statement - $$1$$ and Statement - $$2$$. of the four choices given after the statements, choose the one that best describes the two statements.

Statement - $$1$$:

For a mass $$M$$ kept at the center of a cube of side $$'a'$$, the flux of gravitational field passing through its sides $$4\,\pi \,GM.$$

Statement - 2:

If the direction of a field due to a point source is radial and its dependence on the distance $$'r'$$ from the source is given as $${1 \over {{r^2}}},$$ its flux through a closed surface depends only on the strength of the source enclosed by the surface and not on the size or shape of the surface.

Consider a uniform square plate of side $$' a '$$ and mass $$'m'$$. The moment of inertia of this plate about an axis perpendicular to its plane and passing through one of its corners is

An athlete in the olympic games covers a distance of $$100$$ $$m$$ in $$10$$ $$s.$$ His kinetic energy can be estimated to be in the range

A block of mass $$0.50$$ $$kg$$ is moving with a speed of $$2.00$$ $$m{s^{ - 1}}$$ on a smooth surface. It strike another mass of $$1.0$$ $$kg$$ and then they move together as a single body. The energy loss during the collision is :

Two full turns of the circular scale of a screw gauge cover a distance of 1 mm on its main scale. The total number of divisions on the circular scale is 50. Further, it is found that the screw gauge has a zero error of − 0.03 mm while measuring the diameter of a thin wire, a student notes the main scale reading of 3 mm and the number of circular scale divisions in line with the main scale as 35. The diameter of the wire is

A body of mass m = 3.513 kg is moving along the x-axis with a speed of 5.00 ms⁻¹. The magnitude of its momentum is recorded as

The dimension of magnetic field in M, L, T and C (coulomb) is given as