1
Let $$f:( - 1,1) \to B$$, be a function defined by
$$f\left( x \right) = {\tan ^{ - 1}}{{2x} \over {1 - {x^2}}}$$,
then $$f$$ is both one-one and onto when B is the interval
2
A real valued function f(x) satisfies the functional equation
f(x - y) = f(x)f(y) - f(a - x)f(a + y)
where a is given constant and f(0) = 1, f(2a - x) is equal to
3
A function is matched below against an interval where it is supposed to be
increasing. Which of the following pairs is incorrectly matched?
4
Suppose $$f(x)$$ is differentiable at x = 1 and
$$\mathop {\lim }\limits_{h \to 0} {1 \over h}f\left( {1 + h} \right) = 5$$, then $$f'\left( 1 \right)$$ equals
5
Let $$\alpha$$ and $$\beta$$ be the distinct roots of $$a{x^2} + bx + c = 0$$, then
$$\mathop {\lim }\limits_{x \to \alpha } {{1 - \cos \left( {a{x^2} + bx + c} \right)} \over {{{\left( {x - \alpha } \right)}^2}}}$$ is equal to
6
If $$f$$ is a real valued differentiable function satisfying
$$\left| {f\left( x \right) - f\left( y \right)} \right|$$ $$ \le {\left( {x - y} \right)^2}$$, $$x, y$$ $$ \in R$$
and $$f(0)$$ = 0, then $$f(1)$$ equals
7
If in a frequency distribution, the mean and median are 21 and 22 respectively, then
its mode is approximately :
8
Let x1, x2,...........,xn be n observations such that
$$\sum {x_i^2} = 400$$ and $$\sum {{x_i}} = 80$$. Then a
possible value of n among the following is
9
If the roots of the equation $${x^2} - bx + c = 0$$ be two consecutive integers, then $${b^2} - 4c$$ equals
10
The value of $$a$$ for which the sum of the squares of the roots of the equation $${x^2} - \left( {a - 2} \right)x - a - 1 = 0$$
assume the least value is :
11
If the cube roots of unity are 1, $$\omega \,,\,{\omega ^2}$$ then the roots of the equation $${(x - 1)^3}$$ + 8 = 0, are :
12
The value of $$\int\limits_{ - \pi }^\pi {{{{{\cos }^2}} \over {1 + {a^x}}}dx,\,\,a > 0,} $$ is
13
Area of the greatest rectangle that can be inscribed in the
ellipse $${{{x^2}} \over {{a^2}}} + {{{y^2}} \over {{b^2}}} = 1$$
14
A spherical iron ball $$10$$ cm in radius is coated with a layer of ice of uniform thickness that melts at a rate of $$50$$ cm$$^3$$ /min. When the thickness of ice is $$5$$ cm, then the rate at which the thickness of ice decreases is
15
If $${A^2} - A + 1 = 0$$, then the inverse of $$A$$ is :
16
The system of equations
$$\matrix{
{\alpha \,x + y + z = \alpha - 1} \cr
{x + \alpha y + z = \alpha - 1} \cr
{x + y + \alpha \,z = \alpha - 1} \cr
} $$
has no solutions, if $$\alpha $$ is :
17
If $${a_1},{a_2},{a_3},........,{a_n},.....$$ are in G.P., then the determinant
$$$\Delta = \left| {\matrix{
{\log {a_n}} & {\log {a_{n + 1}}} & {\log {a_{n + 2}}} \cr
{\log {a_{n + 3}}} & {\log {a_{n + 4}}} & {\log {a_{n + 5}}} \cr
{\log {a_{n + 6}}} & {\log {a_{n + 7}}} & {\log {a_{n + 8}}} \cr
} } \right|$$$
is equal to :
18
If $${a^2} + {b^2} + {c^2} = - 2$$ and
f$$\left( x \right) = \left| {\matrix{
{1 + {a^2}x} & {\left( {1 + {b^2}} \right)x} & {\left( {1 + {c^2}} \right)x} \cr
{\left( {1 + {a^2}} \right)x} & {1 + {b^2}x} & {\left( {1 + {c^2}} \right)x} \cr
{\left( {1 + {a^2}} \right)x} & {\left( {1 + {b^2}} \right)x} & {1 + {c^2}x} \cr
} } \right|,$$
then f$$(x)$$ is a polynomial of degree :
19
$$\int {{{\left\{ {{{\left( {\log x - 1} \right)} \over {1 + {{\left( {\log x} \right)}^2}}}} \right\}}^2}\,\,dx} $$ is equal to
20
If $${I_1} = \int\limits_0^1 {{2^{{x^2}}}dx,{I_2} = \int\limits_0^1 {{2^{{x^3}}}dx,\,{I_3} = \int\limits_1^2 {{2^{{x^2}}}dx} } } $$ and $${I_4} = \int\limits_1^2 {{2^{{x^3}}}dx} $$ then
21
The area enclosed between the curve $$y = {\log _e}\left( {x + e} \right)$$ and the coordinate axes is :
22
The parabolas $${y^2} = 4x$$ and $${x^2} = 4y$$ divide the square region bounded by the lines $$x=4,$$ $$y=4$$ and the coordinate axes. If $${S_1},{S_2},{S_3}$$ are respectively the areas of these parts numbered from top to bottom ; then $${S_1},{S_2},{S_3}$$ is :
23
Let $$f(x)$$ be a non - negative continuous function such that the area bounded by the curve $$y=f(x),$$ $$x$$-axis and the ordinates $$x = {\pi \over 4}$$ and $$x = \beta > {\pi \over 4}$$ is $$\left( {\beta \sin \beta + {\pi \over 4}\cos \beta + \sqrt 2 \beta } \right).$$ Then $$f\left( {{\pi \over 2}} \right)$$ is
24
If $${\cos ^{ - 1}}x - {\cos ^{ - 1}}{y \over 2} = \alpha ,$$ then $$4{x^2} - 4xy\cos \alpha + {y^2}$$ is equal to :
25
The value of integral, $$\int\limits_3^6 {{{\sqrt x } \over {\sqrt {9 - x} + \sqrt x }}} dx $$ is
26
The differential equation representing the family of curves $${y^2} = 2c\left( {x + \sqrt c } \right),$$ where $$c>0,$$ is a parameter, is of order and degree as follows:
27
If $$x{{dy} \over {dx}} = y\left( {\log y - \log x + 1} \right),$$ then the solution of the equation is :
28
Three houses are available in a locality. Three persons apply for the houses. Each applies for one house without consulting others. The probability that all the three apply for the same house is :
29
A random variable $$X$$ has Poisson distribution with mean $$2$$.
Then $$P\left( {X > 1.5} \right)$$ equals :
30
Let $$A$$ and $$B$$ two events such that $$P\left( {\overline {A \cup B} } \right) = {1 \over 6},$$ $$P\left( {A \cap B} \right) = {1 \over 4}$$ and $$P\left( {\overline A } \right) = {1 \over 4},$$ where $${\overline A }$$ stands for complement of event $$A$$. Then events $$A$$ and $$B$$ are :
31
If $$C$$ is the mid point of $$AB$$ and $$P$$ is any point outside $$AB,$$ then :
32
Let $$a, b$$ and $$c$$ be distinct non-negative numbers. If the vectors $$a\widehat i + a\widehat j + c\widehat k,\,\,\widehat i + \widehat k$$ and $$c\widehat i + c\widehat j + b\widehat k$$ lie in a plane, then $$c$$ is :
33
The angle between the lines $$2x=3y=-z$$ and $$6x=-y=-4z$$ is :
34
If a vertex of a triangle is $$(1, 1)$$ and the mid points of two sides through this vertex are $$(-1, 2)$$ and $$(3, 2)$$ then the centroid of the triangle is :
35
If $${z_1}$$ and $${z_2}$$ are two non-zero complex numbers such that $$\,\left| {{z_1} + {z_2}} \right| = \left| {{z_1}} \right| + \left| {{z_2}} \right|$$, then arg $${z_1}$$ - arg $${z_2}$$ is equal to :
36
If $$\,\omega = {z \over {z - {1 \over 3}i}}\,$$ and $$\left| \omega \right| = 1$$, then $$z$$ lies on :
37
In a triangle $$PQR,\;\;\angle R = {\pi \over 2}.\,\,If\,\,\tan \,\left( {{P \over 2}} \right)$$ and $$ \tan \left( {{Q \over 2}} \right)$$ are the roots of $$a{x^2} + bx + c = 0,\,\,a \ne 0$$ then
38
If both the roots of the quadratic equation $${x^2} - 2kx + {k^2} + k - 5 = 0$$ are less than 5, then $$k$$ lies in the interval
39
If the letter of the word SACHIN are arranged in all possible ways and these words are written out as in dictionary, then the word SACHIN appears at serial number
40
If the coefficient of $${x^7}$$ in $${\left[ {a{x^2} + \left( {{1 \over {bx}}} \right)} \right]^{11}}$$ equals the coefficient of $${x^{ - 7}}$$ in $${\left[ {ax - \left( {{1 \over {b{x^2}}}} \right)} \right]^{11}}$$, then $$a$$ and $$b$$ satisfy the relation
41
If $$x$$ is so small that $${x^3}$$ and higher powers of $$x$$ may be neglected, then $${{{{\left( {1 + x} \right)}^{{3 \over 2}}} - {{\left( {1 + {1 \over 2}x} \right)}^3}} \over {{{\left( {1 - x} \right)}^{{1 \over 2}}}}}$$ may be approximated as
42
If the coefficients of rth, (r+1)th, and (r + 2)th terms in the binomial expansion of $${{\rm{(1 + y )}}^m}$$ are in A.P., then m and r satisfy the equation
43
If $$x = \sum\limits_{n = 0}^\infty {{a^n},\,\,y = \sum\limits_{n = 0}^\infty {{b^n},\,\,z = \sum\limits_{n = 0}^\infty {{c^n},} } } \,\,$$ where a, b, c are in A.P and $$\,\left| a \right| < 1,\,\left| b \right| < 1,\,\left| c \right| < 1$$ then x, y, z are in
44
The line parallel to the $$x$$ - axis and passing through the intersection of the lines $$ax + 2by + 3b = 0$$ and $$bx - 2ay - 3a = 0,$$ where $$(a, b)$$ $$ \ne $$ $$(0, 0)$$ is :
45
If a circle passes through the point (a, b) and cuts the circle $${x^2}\, + \,{y^2} = {p^2}$$ orthogonally, then the equation of the locus of its centre is :
46
If the circles $${x^2}\, + \,{y^2} + \,2ax\, + \,cy\, + a\,\, = 0$$ and $${x^2}\, + \,{y^2} - \,3ax\, + \,dy\, - 1\,\, = 0$$ intersect in two ditinct points P and Q then the line 5x + by - a = 0 passes through P and Q for :
47
If the pair of lines $$a{x^2} + 2\left( {a + b} \right)xy + b{y^2} = 0$$ lie along diameters of a circle and divide the circle into four sectors such that the area of one of the sectors is thrice the area of another sector then :
48
An ellipse has $$OB$$ as semi minor axis, $$F$$ and $$F$$' its focii and theangle $$FBF$$' is a right angle. Then the eccentricity of the ellipse is :
49
Let $$P$$ be the point $$(1, 0)$$ and $$Q$$ a point on the parabola $${y^2} = 8x$$. The locus of mid point of $$PQ$$ is :
50
The value of $$a$$ for which the sum of the squares of the roots of the equation
$${x^2} - \left( {a - 2} \right)x - a - 1 = 0$$ assume the least value is
51
Let $$f:R \to R$$ be a differentiable function having $$f\left( 2 \right) = 6$$,
$$f'\left( 2 \right) = \left( {{1 \over {48}}} \right)$$. Then $$\mathop {\lim }\limits_{x \to 2} \int\limits_6^{f\left( x \right)} {{{4{t^3}} \over {x - 2}}dt} $$ equals :
52
If the roots of the equation $${x^2} - bx + c = 0$$ be two consecutive integers, then $${b^2} - 4c$$ equals
53
For any vector $${\overrightarrow a }$$ , the value of $${\left( {\overrightarrow a \times \widehat i} \right)^2} + {\left( {\overrightarrow a \times \widehat j} \right)^2} + {\left( {\overrightarrow a \times \widehat k} \right)^2}$$ is equal to :
54
If non zero numbers $$a, b, c$$ are in $$H.P.,$$ then the straight line $${x \over a} + {y \over b} + {1 \over c} = 0$$ always passes through a fixed point. That point is :
55
Let $R=\{(3,3),(6,6),(9,9),(12,12),(6,12)$, $(3,9),(3,12),(3,6)\}$ be a relation on the set $A=\{3,6,9,12\}$. The relation is :
56
A lizard, at an initial distance of 21 cm behind an insect moves from rest with an acceleration of $2 \mathrm{~cm} / \mathrm{s}^2$ and pursues the insect which is crawling uniformly along a straight line at a speed of $20 \mathrm{~cm} / \mathrm{s}$. Then the lizard will catch the insect after :
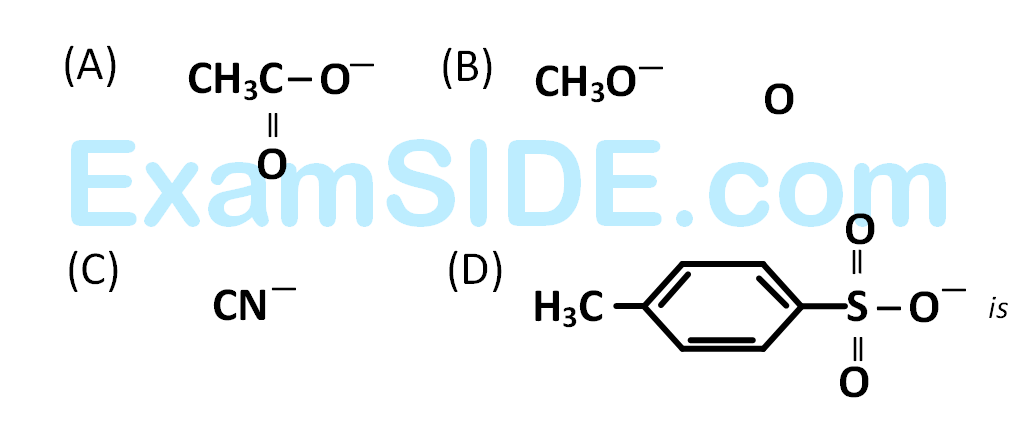

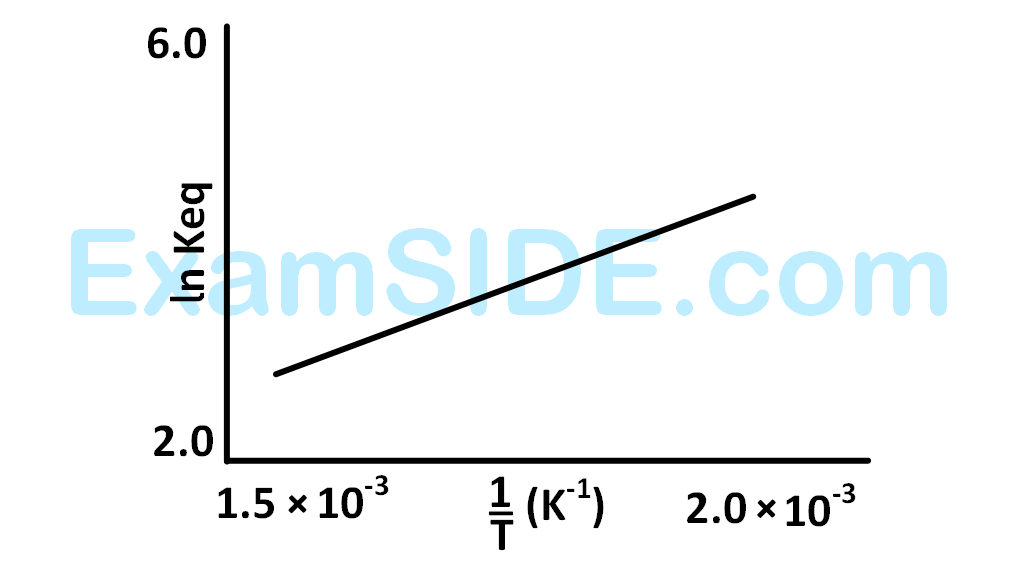
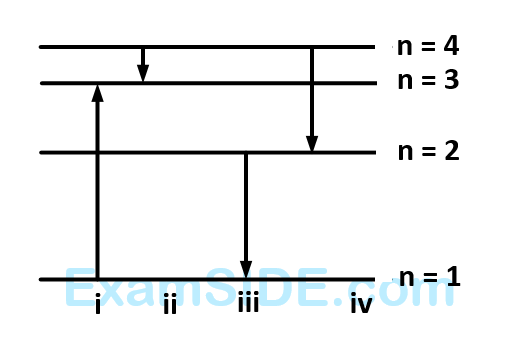
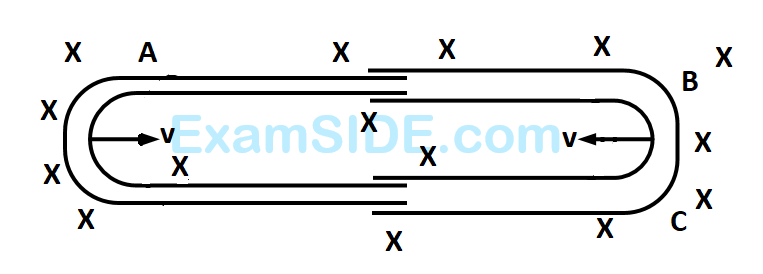
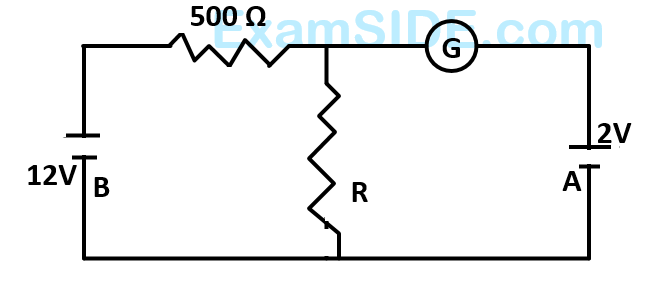
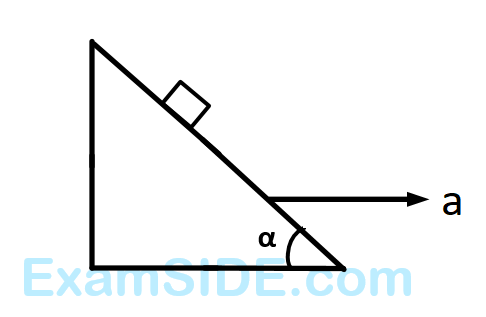
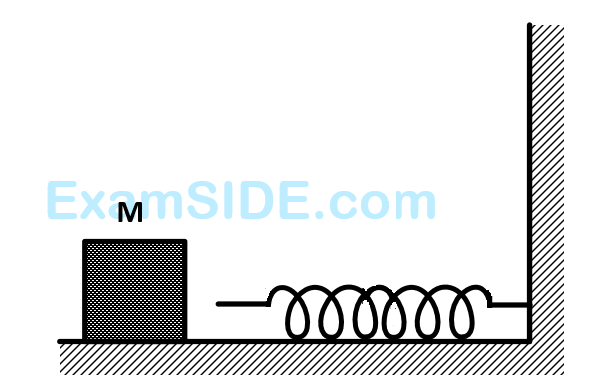
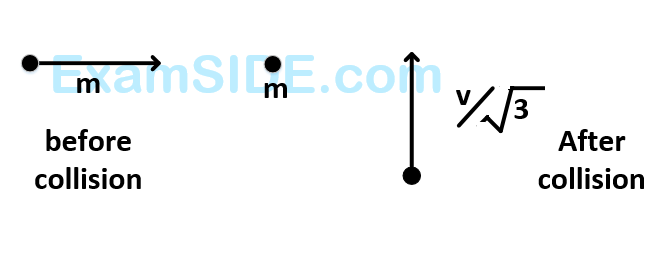
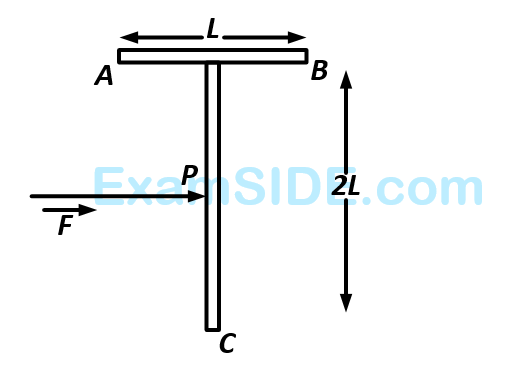
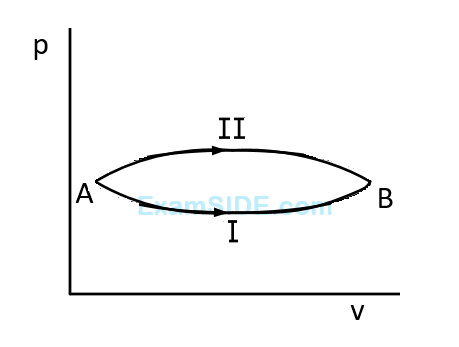

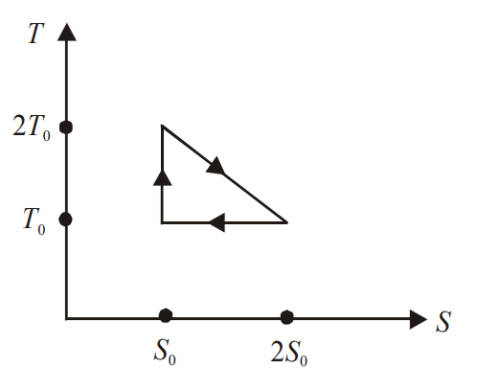
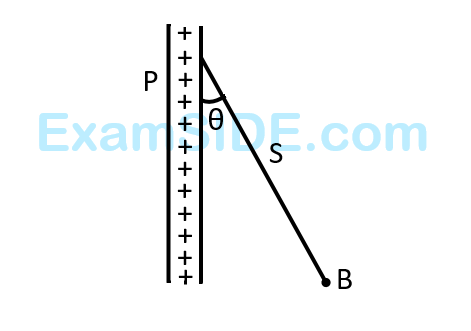 f
f