For the circuit shown in the figure below, it is given that $${V_{CE}} = {{{V_{CC}}} \over 2}.$$ The transistor has $$\beta = 29$$ and $${V_{BE}} = 0.7\,\,V$$ when the $$B$$-$$E$$ junction is forward biased.

For this circuit, the value of $${{{R_B}} \over R}$$ is

For the circuit shown below, assume that the $$OPAMP$$ is ideal.

Which one of the following is TRUE?

When a unit ramp input is applied to the unity feedback system having closed loop transfer function $${{C\left( s \right)} \over {R\left( s \right)}} = {{Ks + b} \over {{s^2} + as + b}},\,\left( {a > 0,\,b > 0,\,K > 0} \right),$$ the steady state error will be

The range of K for which all the roots of the equation $${s^3} + 3{s^2} + 2s + K = 0$$ are in the left half of the complex $$s$$-plane is

The root locus of the feedback control system having the characteristic equation $${s^2} + 6Ks + 2s + 5 = 0$$ where $$K>0,$$ enters into the real axis at

The transfer function $$C(s)$$ of a compensator is given below: $$C\left( s \right) = {{\left( {1 + {s \over {0.1}}} \right)\left( {1 + {s \over {100}}} \right)} \over {\left( {1 + s} \right)\left( {1 + {s \over {10}}} \right)}}$$

The frequency range in which the phase (lead) introduce by the compensator reaches the maximum is

Consider the system described by the following state space representation
$$\eqalign{ & \left[ {\matrix{ {\mathop {{x_1}}\limits^ \bullet \left( t \right)} \cr {\mathop {{x_2}}\limits^ \bullet \left( t \right)} \cr } } \right] = \left[ {\matrix{ 0 & 1 \cr 0 & { - 2} \cr } } \right]\left[ {\matrix{ {{x_1}\left( t \right)} \cr {{x_2}\left( t \right)} \cr } } \right] + \left[ {\matrix{ 0 \cr 1 \cr } } \right]u\left( t \right) \cr & y\left( t \right) = \left[ {\matrix{ 1 & 0 \cr } } \right]\left[ {\matrix{ {{x_1}\left( t \right)} \cr {{x_2}\left( t \right)} \cr } } \right] \cr} $$

If $$u(t)$$ is a unit step input and $$\left[ {\matrix{ {{x_1}\left( 0 \right)} \cr {{x_2}\left( 0 \right)} \cr } } \right] = \left[ {\matrix{ 1 \cr 0 \cr } } \right],$$ the value of output $$y(t)$$ at $$t=1$$ sec (rounded off to three decimal places) is _____________.

For a $$3$$ -input logic circuit shown below, the output $$Z$$ can be expressed as

For the synchronous sequential circuit shown below, the output $$Z$$ is zero for the initial conditions $${Q_A}{Q_B}{Q_C} = Q{'_A}Q{'_B}Q{'_C} = 100.$$

The minimum number if clock cycles after which the output $$Z$$ would again become zero is _____________.

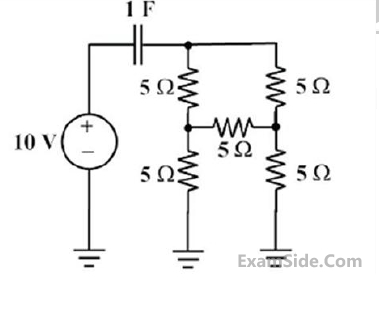
The initial charge in the 1 F capacitor present in the circuit shown is zero. The energy in joules transferred from the DC source until steady state condition is reached equals ______. (Give the answer up to one decimal place.)

The mean square value of the given periodic waveform f(t) is_________.

In the circuit shown below, the value of capacitor C required for maximum power to be transferred to the load is

For the balanced Y-Y connected 3-Phase circuit shown in the figure below, the line-line voltage is 208 V rms and the total power absorbed by the load is 432 W at a power factor of 0.6 leading. The approximate value of the impedance Z is

For the given 2-port network, the value of transfer impedance Z₂₁ in ohms is_______.

For the network given in figure below, the Thevenin's voltage V_ab is

Two resistors with nominal resistance values $${R_1}$$ and $${R_2}$$ have additive uncertainties $$\Delta {R_1}$$ and $$\Delta {R_2},$$ respectively. When these resistances are connected in parallel, the standard deviation of the error in the equivalent resistance $$R$$ is

A stationary closed Lissajous pattern on an oscilloscope has $$3$$ horizontal tangencies and $$2$$ vertical tangencies for a horizontal input with frequency $$3$$ $$kHZ.$$ The frequency of the vertical input is

A $$10{\raise0.5ex\hbox{$\scriptstyle 1$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 2$}}$$ digit timer counter possesses a base clock of frequency $$100$$ $$MHz$$. When measuring a particular input, the reading obtained is the same in: (i) Frequency mode of operation with a gating time of one second and (ii) Period mode of operation (in the $$ \times \,\,\,10$$ ns scale). The frequency of the unknown input (reading obtained) in $$Hz$$ is _______.

A $$3$$-phase, $$2$$-pole, $$50$$ $$Hz,$$ synchronous generator has a rating of $$250$$ $$MVA,$$ $$0.8$$ $$pf$$ lagging. The kinetic energy of the machine at synchronous speed is $$100$$ $$MJ.$$ The machine is running steadily at synchronous speed and delivering $$60$$ $$MW$$ power at a power angle of $$10$$ electrical degrees. If the load is suddenly removed, assuming the acceleration is constant for $$10$$ cycles, the value of the power angle after $$5$$ cycles is ________ electrical degrees.

Two generating units rated $$300$$ $$MW$$ and $$400$$ $$MW$$ have governor speed regulation of $$6\% $$ and $$4\% $$ respectively from no load to full load. Both the generating units are operating in parallel to share a load of $$600$$ $$MW.$$ Assuming free governor action, the load shared by the larger unit is _______ $$MW.$$

A $$25$$ $$kVA,$$ $$400$$ $$V,$$ $$\Delta $$ - connected, $$3$$-phase, cylindrical rotor synchronous generator requires a field current of $$5$$ $$A$$ to maintain the rated armature current under short-circuit condition. For the same field current, the open-circuit voltage is $$360$$ $$V.$$ Neglecting the armature resistance and magnetic saturation, its voltage regulation (in $$\% $$ with respect to terminal voltage), when the generator delivers the rated load at $$0.8$$ $$pf$$ leading, at rated terminal voltage is ____________.

If the primary line voltage rating is 3.3 kV (Y side) of a 25 kVA. $$Y-\triangle$$ transformer (the per phase turns ratio is 5:1), then the line current rating of the secondary side (in Ampere) is_______.

A 120 V DC shunt motor takes 2 A at no load. It takes 7 A on full load while running at 1200 rpm. The armature resistance is 0.8 Ω, and the shunt field resistance is 240 Ω. The no load speed, in rpm, is _________.

A 220 V, 10 kW, 900 rpm separately excited DC motor has an armature resistance R_a= 0.02 Ω. When the motor operates at rated speed and with rated terminal voltage, the electromagnetic torque developed by the motor is 70 Nm. Neglecting the rotational losses of the machine, the current drawn by the motor from the 220 V supply is

A 3-phase, 4-pole, 400 V, 50 Hz squirrel-cage induction motor is operating at a slip of 0.02. The speed of the rotor flux in mechanical rad/sec, sensed by a stationary observer, is closest to

A star-connected, 12.5 kW, 208 V (line), 3-phase, 60 Hz squirrel cage induction motor has following equivalent circuit parameters per phase referred to the stator. R₁ = 0.3 Ω, R₂ = 0.3 Ω, X₁ = 0.41 Ω, X₂ = 0.41 Ω. Neglect shunt branch in the equivalent circuit. The starting current (in Ampere) for this motor when connected to an 80 V (line), 20 Hz, 3- phase AC source is __________.

If a synchronous motor is running at a leading power factor, its excitation induced voltage (E_r) is

A thin soap bubble of radius R = 1 cm, and thickness a = 3.3 µm(a << R), is at a potential of 1 V with respect to a reference point at infinity. The bubble bursts and becomes a single spherical drop of soap (assuming all the soap is contained in the drop) of radius r. The volume of the soap in the thin bubble is $$4\mathrm{πR}^2\mathrm a$$ and that of the drop is $$\frac43\mathrm{πr}^3$$. The potential in volts, of the resulting single spherical drop with respect to the same reference point at infinity is __________. (Give the answer up to two decimal places.)

Consider a solid sphere of radius 5 cm made of a perfect electric conductor. If one million electrons are added to this sphere, these electrons will be distributed.

The figures show diagrammatic representations of vector fields $$\overrightarrow X,\;\overrightarrow Y,\;and\;\overrightarrow Z$$ respectively. Which one of the following choices is true?

The value of the contour integral in the complex - plane $$\oint {{{{z^3} - 2z + 3} \over {z - 2}}} dz$$ along the contour $$\left| z \right| = 3,$$ taken counter-clockwise is

The eigen values of the matrix given below are $$\left[ {\matrix{ 0 & 1 & 0 \cr 0 & 0 & 1 \cr 0 & { - 3} & { - 4} \cr } } \right]$$

Let $$\,{y^2} - 2y + 1 = x$$ and $$\,\sqrt x + y = 5.\,\,$$ The value of $$\,x + \sqrt y \,\,$$ equals ________. (Given the answer up to three decimal places)

Consider a function $$f\left( {x,y,z} \right)$$ given by $$f\left( {x,y,z} \right) = \left( {{x^2} + {y^2} - 2{z^2}} \right)\left( {{y^2} + {z^2}} \right).$$ The partial derivative of this function with respect to $$x$$ at the point $$x=2, y=1$$ and $$z=3$$ is _______.

Let $$x$$ and $$y$$ be integers satisfying the following equations $$$2{x^2} + {y^2} = 34$$$ $$$x + 2y = 11$$$
The value of $$(x+y)$$ is _________.

Let $$g\left( x \right) = \left\{ {\matrix{ { - x} & {x \le 1} \cr {x + 1} & {x \ge 1} \cr } } \right.$$ and
$$f\left( x \right) = \left\{ {\matrix{ {1 - x,} & {x \le 0} \cr {{x^{2,}}} & {x > 0} \cr } } \right..$$
Consider the composition of $$f$$ and $$g,$$ i.e., $$\left( {f \circ g} \right)\left( x \right) = f\left( {g\left( x \right)} \right).$$ The number of discontinuities in $$\left( {f \circ g} \right)\left( x \right)$$ present in the interval $$\left( { - \infty ,0} \right)$$ is

An urn contains $$5$$ red balls and $$5$$ black balls. In the first draw, one ball is picked at random and discarded without noticing its colour. The probability to get a red ball in the second draw is

Assume that in a traffic junction, the cycle of the traffic signal lights is $$2$$ minutes of green (vehicle does not stop) and $$3$$ minutes of red (vehicle stops). Consider that the arrival time of vehicles at the junction is uniformly distributed over $$5$$ minute cycle. The expected waiting time (in minutes) for the vehicle at the junction is _________.

A person decides to toss a fair coin repeatedly until he gets a head. He will make at most $$3$$ tosses. Let the random variable $$Y$$ denotes the number of heads. The value of var $$\left\{ Y \right\},$$ where var $$\left\{ . \right\}$$ denotes the variance, equal

In the circuit shown, the diodes are ideal, the inductance is small, and $${{\rm I}_0} \ne 0.$$ Which one of the following statements is true?

A phase-controlled, single-phase, full-bridge converter is fed from a $$230$$ $$V,$$ $$50$$ $$Hz,$$ $$AC$$ source. The fundamental frequency in $$Hz$$ of the voltage ripple on the $$DC$$ side is

The figure below shows the circuit diagram of a controlled rectifier supplied from a $$230V,$$ $$50$$ $$Hz,$$ $$1$$-phase voltage source and a $$10:1$$ ideal transformer. Assume that all devices are ideal. The firing angles of the thyristors $${T_1}$$ and $${T_2}$$ are $${90^ \circ }$$ and $${270^ \circ },$$ respectively.

The $$RMS$$ value of the current through diode $${D_3}$$ in amperes is ________________.

In the circuit shown all elements are ideal and the switch $$S$$ is operated at $$10$$ $$kHz$$ and $$60$$% duty ratio. The capacitor is large enough so that the ripple across it is negligible and at steady state acquires a voltage as shown. The peak current in amperes drawn from the $$50$$ $$V$$ $$DC$$ source is ________. (Give the answer up to one decimal place.)

A three-phase voltage source inverter with ideal devices operating in $${180^ \circ }$$ conduction mode is feeding a balanced star-connected resistive load. The $$DC$$ voltage input is $${V_{dc}}.$$ The peak of the fundamental component of the phase voltage is

The figure below shows a half-bridge voltage source inverter supplying an $$RL$$-load with $$R = 40\,\,\Omega $$ and $$L = \left( {{{0.3} \over \pi }} \right)H.$$ The desired fundamental frequency of the load voltage is $$50$$ $$Hz.$$ The switch control signals of the converter are generated using sinusoidal pulse width modulation with modulation index. $$M = 0.6.$$ at $$50$$ $$Hz$$, the$$RL$$-load draws an active power of $$1.44$$ $$kW.$$ The value of $$DC$$ source volts is

A 3-phase, 2-pole, 50 Hz, synchronous generator has a rating of 250 MVA, 0.8 pf lagging. The kinetic energy of the machine at synchronous speed is 1000 MJ. The machine is running steadily at synchronous speed and delivering 60 MW power at a power angle of 10 electrical degrees. If the load is suddenly removed, assuming the acceleration is constant for 10 cycles, the value of the power angle after 5 cycles is ________ electrical degrees.

The figure show the per-phase representation of a phase-shifting transformer connected between buses $$1$$ and $$2,$$ where $$\alpha $$ is a complex number with non-zero real and imaginary parts.
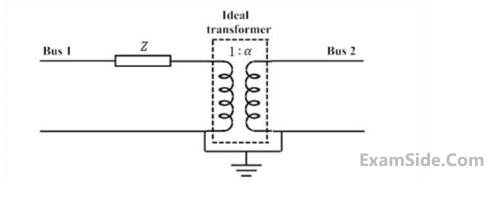
For the given circuit, $${Y_{bus}}$$ and $${Z_{bus}}$$ are bus admittance matrix and bus impedance matrix, respectively, each of size $$2\, \times \,2$$. Which one of the following statements is true?

In a load flow problem solved by Newton-Raphson method with polar coordinates, the size of the Jacobian is $$\,100\,\, \times \,\,100.$$ If there are $$20$$ PV buses in addition to PQ buses and a slack bus, the total number of buses in the system is ________.

A 3-phase 50 Hz generator supplies power of 3 MW at 17.32 kV to a balanced 3-phase inductive load through an overhead line. The per phase line resistance and reactance are 0.25 $$\Omega $$ and 3.925 $$\Omega $$ respectively. If the voltage at the generator terminal is 17.87 kV, the power factor of the load is ________.

The normal - $$\pi $$ circuit of a transmission line is shown in the figure.

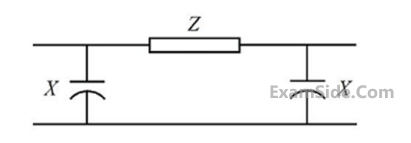
Impedance $$Z = 100\angle {80^ \circ }$$ and reactance $$\,X = 3300\Omega .$$ The magnitude of the characteristic impedance of the transmission line, in $$\Omega ,$$ is ________. (Give the answer up to one decimal place.)

The output y(t) of the following system is to be sampled, so as to reconstruct it from its samples uniquely. The required minimum sampling rate is

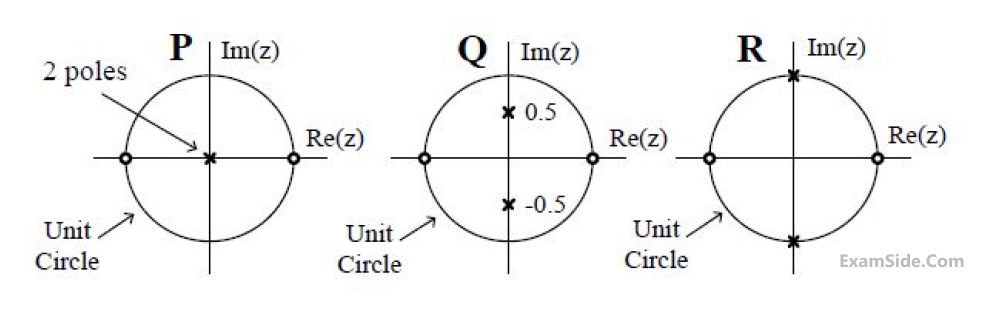
The pole-zero plots of three discrete-time systems P, Q and R on the z-plane are shown below. Which one of the following is TRUE about the frequency selectivity of these systems?

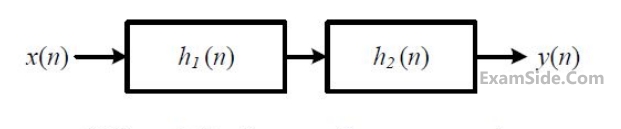
A cascade system having the impulse responses $$$\begin{array}{l}h_1\left(n\right)=\left\{1,\;-1\right\}\;\;\;and\;\;h_2\left(n\right)=\left\{1,\;1\right\}\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\uparrow\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\uparrow\end{array}$$$ is shown in the figure below, where symbol $$\uparrow$$ denotes the time origin. The input sequence x(n) for which the cascade system produces an output sequence $$$\begin{array}{l}y\left(n\right)=\left\{1,\;2,\;1,\;-1,\;-2,\;-1\right\}\;\;is\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\uparrow\end{array}$$$