1
In the circuit shown below, the knee current of the ideal Zener diode is $$10$$ $$mA.$$ To maintain $$5 V$$ across $${R_L}$$, the minimum value of $${R_L}$$ in $$\Omega $$ and the minimum power rating of the Zener diode in $$mW$$ respectively are

2
A voltage $$1000\sin \omega t$$ Volts is applied across $$YZ.$$ Assuming ideal diodes, the voltage measured across $$WX$$ in Volts is

3
In the circuit shown below what is the output voltage $$\left( {{V_{out}}} \right)$$ in Volts If a silicon transfer $$Q$$ and an ideal op-amp are used?

4
In the circuit shown below the op-amps are ideal. Then $${V_{out}}$$ in Volts is

5
In the feedback network shown below, if the feedback factor $$k$$ is increased, then the

6
The state variable formulation of a system is given as
$$\left[ {\matrix{
{\mathop {{x_1}}\limits^ \bullet } \cr
{\mathop {{x_2}}\limits^ \bullet } \cr
} } \right] = \left[ {\matrix{
{ - 2} & 0 \cr
0 & { - 1} \cr
} } \right]\left[ {\matrix{
{{x_1}} \cr
{{x_2}} \cr
} } \right] + \left[ {\matrix{
1 \cr
1 \cr
} } \right]u,\,\,{x_1}\left( 0 \right) = 0,$$
$${x_2}\left( 0 \right) = 0$$ and $$y = \left[ {\matrix{
1 & 0 \cr
} } \right]\left[ {\matrix{
{{x_1}} \cr
{{x_2}} \cr
} } \right]$$
The system is
7
The transfer function $${{{V_2}\left( s \right)} \over {{V_1}\left( s \right)}}$$ of the circuit shown below is

8
The signal flow graph for a system is given below. The transfer function $${{Y\left( s \right)} \over {U\left( s \right)}}$$ for this system is

9
The open-loop transfer function of a $$dc$$ motor is given as $${{\omega \left( s \right)} \over {{V_a}\left( s \right)}} = {{10} \over {1 + 10s}}.$$ When connected in feedback as shown below, the approximate value of $${K_a}$$ that will reduce the time constant of the closed loop system by one hundred times as compared to that of the open-loop system is
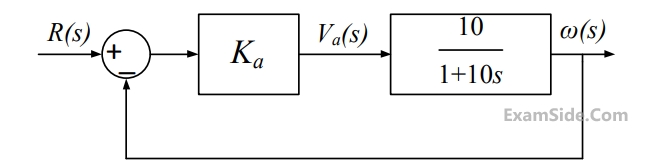
10
The Bode plot of a transfer function $$G(s)$$ is shown in the figure below.
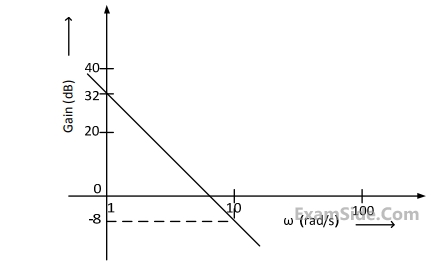
The gain is $$\left( {20\log \left| {G\left( s \right)} \right|} \right)$$ is $$32$$ $$dB$$ and $$–8$$ $$dB$$ at $$1$$ $$rad/s$$ and $$10$$ $$rad/s$$ respectively. The phase is negative for all $$\omega .$$ Then $$G(s)$$ is
11
The state variable formulation of a system is given as
$$\left[ {\matrix{
{\mathop {{x_1}}\limits^ \bullet } \cr
{\mathop {{x_2}}\limits^ \bullet } \cr
} } \right] = \left[ {\matrix{
{ - 2} & 0 \cr
0 & { - 1} \cr
} } \right]\left[ {\matrix{
{{x_1}} \cr
{{x_2}} \cr
} } \right] + \left[ {\matrix{
1 \cr
1 \cr
} } \right]u,\,\,{x_1}\left( 0 \right) = 0,$$
$${x_2}\left( 0 \right) = 0$$ and $$y = \left[ {\matrix{
1 & 0 \cr
} } \right]\left[ {\matrix{
{{x_1}} \cr
{{x_2}} \cr
} } \right]$$
The response $$y(t)$$ to a unit step input is
12
A bulb in staircase has two switches, one switch being at the ground floor and the other one at the first floor. The bulb can be turned $$ON$$ and also can be turned $$OFF$$ by any one of the switches irrespective of the state of the other switch. The logic of switching of the bulb resembles
13
The clock frequency applied to the digital circuit shown in the figure below is $$1$$ $$kHz.$$ If the initial state of the output $$Q$$ of the flip-flop is $$‘0’,$$ then the frequency of the output waveform $$Q$$ in $$kHz$$ is

14
Three capacitors C
1, C
2 and C
3 whose values are 10μF, 5μF and 2μF
respectively, have breakdown voltages of 10V, 5V and 2V respectively. For the
interconnection shown, the maximum safe voltage in Volts that can be applied
across the combination and the corresponding total charge in μC stored in the
effective capacitance across the terminals are respectively

15
A source $$v_s\left(t\right)=V\cos100\mathrm{πt}$$ has an internal impedance of (4 + j3) Ω.If a purely
resistive load connected to this source has to extract the maximum power out of
the source, its value in Ω should be
16
In the circuit shown below, if the source voltage $$V_s=100\angle53.12^\circ\;V$$ then the Thevenin’s equivalent
voltage in Volts as seen by the load resistance R
L is

17
Two magnetically uncoupled inductive coils have Q factors q1 and q2 at the
chosen operating frequency. Their respective resistances are R1 and R2 . When
connected in series, their effective Q factor at the same operating frequency is
18
Consider a delta connection of resistors and it's equivalent star connection as
shown below. If all elements of the delta connection are scaled by a factor k,
k>0, the elements of the corresponding star equivalent will be scaled by a factor
of

19
The input impedance of the permanent magnet moving coil $$(PMMC)$$ voltmeter is infinite. Assuming that the diode shown in the figure below is ideal, the reading of the voltmeter in Volts is

20
Three moving iron type voltmeters are connected as shown below. Voltmeter readings are $$V,$$ $${V_1}$$ and $${V_2}$$ , as indicated. The correct relation among the voltmeter readings is

21
A strain gauge forms one arm of the bridge shown in the figure below and has a nominal resistance without any load as $$\,{R_s} = 300\Omega .$$ Other bridge resistance are $$\,{R_1} = {R_2} = {R_3} = 300\Omega .\,\,$$ The maximum permissible current through the strain gauge is $$20$$ $$mA.$$ During certain measurement when the bridge is excited by maximum permissible voltage and the strain gauge resistance is increased by $$1$$% over the nominal value, the output voltage $${V_0}$$ in $$mV$$ is

22
A single-phase transformer has no-load loss of 64 W, as obtained from an open circuit
test. When a short-circuit test is performed on it with 90% of the rated
currents flowing in its both LV and HV windings, he measured loss is 81 W. The
transformer has maximum efficiency when operated at
23
The following arrangement consists of an ideal transformer and an attenuator
which attenuates by a factor of 0.8. An ac voltage V
WX1 = 100V is applied across
WX to get an open circuit voltage V
YZ1 across YZ. Next, an ac voltage V
YZ2 =100V is
applied across YZ to get an open circuit voltage V
WX2 across WX. Then,
$$\frac{V_{YZ1}}{V_{WX1}}$$, $$\frac{V_{WX2}}{V_{YZ2}}$$
are respectively,

24
Leakage flux in an induction motor is
25
A 4-pole induction motor, supplied by a slightly unbalanced three-phase 50Hz
source, is rotating at 1440 rpm. The electrical frequency in Hz of the induced
negative sequence current in the rotor is
26
A dielectric slab with 500 mm x 500 mm cross-section is 0.4 m long. The slab is
subjected to a uniform electric field of $$E=6{\widehat a}_x+8{\widehat a}_y$$ kV /mm. The relative
permittivity of the dielectric material is equal to 2. The value of constant $$\varepsilon_0$$ is
$$8.85\times10^{-12}\;F/m$$ . The energy stored in the dielectric in Joules is
27
The flux density at a point in space is given by
$$\overrightarrow B=\;4x{\widehat a}_x\;+\;2ky{\widehat a}_y\;+\;8{\widehat a}_z\;\;Wb/m^2$$.
The value of constant k must be equal to
28
Square roots of $$-i,$$ where $$i = \sqrt { - 1} $$ are
29
$$\oint {{{{z^2} - 4} \over {{z^2} + 4}}} dz\,\,$$ evaluated anticlockwise around the circular $$\left| {z - i} \right| = 2,$$ where $$i = \sqrt { - 1} $$, is
30
The equation $$\left[ {\matrix{
2 & { - 2} \cr
1 & { - 1} \cr
} } \right]\left[ {\matrix{
{{x_1}} \cr
{{x_2}} \cr
} } \right] = \left[ {\matrix{
0 \cr
0 \cr
} } \right]$$ has
31
A matrix has eigen values $$-1$$ and $$-2.$$ The corresponding eigenvectors are $$\left[ {\matrix{
1 \cr
{ - 1} \cr
} } \right]$$ and $$\left[ {\matrix{
1 \cr
{ - 2} \cr
} } \right]$$ respectively. The matrix is
32
A function $$y = 5{x^2} + 10x\,\,$$ is defined over an open interval $$x=(1,2).$$ At least at one point in this interval, $${{dy} \over {dx}}$$ is exactly
33
The curl of the gradient of the scalar field defined by $$\,V = 2{x^2}y + 3{y^2}z + 4{z^2}x$$ is
34
Given a vector field $$\overrightarrow F = {y^2}x\widehat a{}_x - yz\widehat a{}_y - {x^2}\widehat a{}_z,$$ the line integral $$\int {F.dl} $$ evaluated along a segment on the $$x-$$axis from $$x=1$$ to $$x=2$$ is
35
A continuous random variable $$X$$ has a probability density function $$f\left( x \right) = {e^{ - x}},0 < x < \infty .$$ Then $$P\left\{ {X > 1} \right\}$$ is
36
When the Newton-Raphson method is applied to solve the equation $$\,\,f\left( x \right) = {x^3} + 2x - 1 = 0,\,\,$$ the solution at the end of the first iteration with the initial value as $${x_0} = 1.2$$ is
37
Thyristor $$T$$ in the figure below is initially off and is triggered with a single pulse of width $$10\mu s.$$ It is given that $$L = \left( {{{100} \over \pi }} \right)\mu H$$ and $$C = \left( {{{100} \over \pi }} \right)\mu F.$$ Assuming latching and holding currents of the thyristor are both zero and the initial charge on $$C$$ is zero, $$T$$ conducts for

38
In the figure shown below, the chopper feeds a resistive load from a battery source. $$MOSFET$$ $$Q$$ is switched at $$250$$ $$kHz,$$ with a duty ratio of $$0.4.$$ All elements of the circuit are assumed to be ideal.

The PEAK-TO-PEAK source current ripple in $$Amps$$ is
39
In the figure shown below, the chopper feeds a resistive load from a battery source. $$MOSFET$$ $$Q$$ is switched at $$250$$ $$kHz,$$ with a duty ratio of $$0.4.$$ All elements of the circuit are assumed to be ideal.

The average source current in Amps in steady-state is
40
The Voltage Source Inverter $$(VSI)$$ shown in the figure below is switched to provide a $$50$$ $$Hz,$$ square-wave $$ac$$ output voltage ($${V_0}$$) across an $$R$$-$$L$$ load. Reference polarity of $${V_0}$$ and reference direction of the output current $${I_0}$$ are indicated in the figure. It is given that $$R = 3\,\,\Omega ,\,\,L = 9.55\,\,mH.$$

Appropriate transition $$i.e,,$$ $$Zero$$ voltage switching $$(ZVS)/Zero$$ current switching $$(ZCS)$$ of the $$IGBTs$$ during turn - on/turn off is
41
The Voltage Source Inverter $$(VSI)$$ shown in the figure below is switched to provide a $$50$$ $$Hz,$$ square-wave $$ac$$ output voltage ($${V_0}$$) across an $$R$$-$$L$$ load. Reference polarity of $${V_0}$$ and reference direction of the output current $${I_0}$$ are indicated in the figure. It is given that $$R = 3\,\,\Omega ,\,\,L = 9.55\,\,mH.$$

In the interval when $${V_0} < 0$$ and $${i_0} > 0$$ the pair of devices which conducts the load current is
42
In the following network, the voltage magnitudes at all buses are equal to $$1$$ p.u., the voltage phase angles are very small, and the line resistance are negligible. All the line reactances are equal to $$j1\Omega .$$
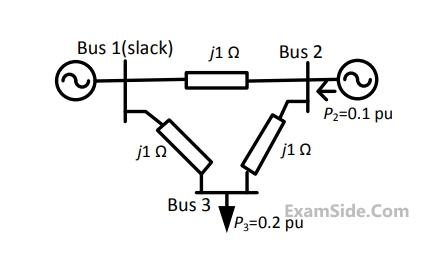
The voltage phase angles in rad at buses $$2$$ and $$3$$ are
43
For a power system network with $$n$$ nodes, $${Z_{33}}$$ of its bus impedance matrix is $$j0.5$$ per unit. The voltage at mode $$3$$ is $$1.3\angle - {10^0}\,\,$$ per unit. If a capacitor having reactance of $$-j3.5$$ per unit is now added to the network between node $$3$$ and the reference node, the current drawn by the capacitor per unit as
44
In the following network, the voltage magnitudes at all buses are equal to $$1$$ p.u., the voltage phase angles are very small, and the line resistance are negligible. All the line reactances are equal to $$j1\Omega .$$

If the base impedance and the line-to-line base voltage are $$100\Omega $$ and $$\,100kV,\,\,$$ respectively, then the real power in MW delivered by the generator connected at the slack bus is
45
The angle $$\delta $$ in the swing equation of a synchronous generator is the
46
A single load is supplied by a single voltage source. If the current flowing from the load to the source is $$10\angle - {150^0}$$ A and if the voltage at the load terminals is $$100\angle {60^0}$$ $$V,$$ then the
47
Which one of the following statements is NOT TRUE for a continuous time causal
and stable LTI system?
48
For a periodic signal the $$v\left(t\right)=30\sin100t\;+\;10\cos300t\;+\;6\sin\left(500t\;+\;\frac{\mathrm\pi}4\right)$$
fundamental frequency in radians/s is
49
Assuming zero initial condition, the response y(t) of the system given below to a
unit step input u(t) is
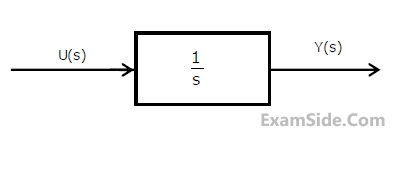
50
Two systems with impulse responses h1(t) and h2(t) are connected in cascade.
Then the overall impulse response of the cascaded system is given by
51
The impulse response of a system is h(t) = tu(t). For an input u(t − 1), the output
is
52
The impulse response of a continuous time system is given by
h(t) = $$\delta$$(t − 1) + $$\delta$$(t − 3). The value of the step response at t = 2 is
53
A band-limited signal with a maximum frequency of 5 kHz is to be sampled.
According to the sampling theorem, the sampling frequency in kHz which is not
valid is




























