Determine the transfer function $$\left( {{{{V_y}} \over {{V_x}}}} \right)$$ for the $$RC$$ network shown in figure $$(1).$$

The network is used as a feedback circuit in an oscillator circuit shown in figure $$(2)$$ to generate sinusoidal oscillations. Assuming that the operational amplifier is ideal, determine the value of $${R_F}$$ for generating these oscillations. Also determine the oscillation frequency if $$R = 10\,\,k\Omega $$ and $$C=100PF$$

The output voltage$$\left( {{V_0}} \right)$$ of the Schmitt trigger shown in figure swings between $$+15V$$ and $$–15V.$$ Assume that the operational amplifier is ideal. The output will change from $$+15V$$ to $$–15V$$ when the instantaneous value of the input sine wave is

For the circuit shown in Figure, $${{\rm I}_E} = 1\,\,mA,\,\,\,\beta = 99$$ and $${V_{BE}} = 0.7\,\,V$$ determine

(a) Current through $${R_1}$$ and $${R_C}$$
(b) The output voltage $${V_0}$$
(c) The value of $${R_F}$$

In the single phase diode bridge rectifier shown in the figure, the load resistor is $$R = 50\,\Omega .$$ The source voltage is $$V=200$$ $$sin$$ $$\omega t,$$ where $$\omega = 2\pi \, \times \,50\,rad/sec.$$ The power dissipated in the load resistor $$R$$ is

A diode whose terminal characteristics are related as $${i_D} = {{\rm I}_S}\,{e^{{V \over {{V_T}}}}},\,$$ where $${{\rm I}_S}$$ is the reverse saturation current and $${V_T}$$ is thermal voltage ($$25$$ $$mV$$) is biased at $${i_D} = 2\,mA.$$ Its dynamic resistance is _______.

The forward resistance of the diode shown in figure is $$5\Omega $$ and the remaining parameters are same as those of ideal diode. The $$DC$$ component of the source current is

The cut in voltage of both Zener diode $${D_z}$$ and diode $$D$$ shown in Figure is $$0.7$$ $$V,$$ while break down voltage of the zener is $$3.3$$ $$V$$ and reverse breakdown voltage of $$D$$ is $$50$$ $$V.$$ the other parameters can be assumed to be the same as those of an ideal diode. The values of the peak output voltage ($${V_0}$$) are

The transfer function of the system described by $${{{d^2}y} \over {d{t^2}}} + {{dy} \over {dt}} = {{du} \over {dt}} + 2u$$ with $$u$$ as input and $$y$$ as output is

Obtain a state variable representation of the system governed by the differential equation: $${{{d^2}y} \over {d{t^2}}} + {{dy} \over {dt}} - 2y = u\left( t \right){e^{ - t}},\,\,\,$$ with the choice of state variables as $${x_1} = y,$$ $${x_2} = \left( {{{dy} \over {dt}} - y} \right){e^t}.$$ Aso find $${x_2}\left( t \right),$$ given that $$u(t)$$ is a unit step function and $${x_2}\left( 0 \right) = 0.$$

For the system $$\mathop X\limits^ \bullet = \left[ {\matrix{ 2 & 0 \cr 0 & 4 \cr } } \right]X + \left[ {\matrix{ 1 \cr 1 \cr } } \right]u;\,\,\,y = \left[ {\matrix{ 4 & 0 \cr } } \right]X,\,$$ with u as unit impulse and with zero initial state, the output, $$y$$, becomes

For the system $$X = \left[ {\matrix{ 2 & 3 \cr 0 & 5 \cr } } \right]X + \left[ {\matrix{ 1 \cr 0 \cr } } \right]u,$$ Which of the following statement is true?

The state transition matrix for the system $$\mathop X\limits^ \bullet = AX\,\,$$ with initial state $$X(0)$$ is

The open loop transfer function of a unity feedback system is given by $$G\left( s \right) = {{2\left( {s + \alpha } \right)} \over {s\left( {s + 2} \right)\left( {s + 10} \right)}}.$$ Sketch the root locus as $$\alpha $$ varies from $$0$$ to $$\infty $$. Find the angle and real axis intercept of the asymptotes, breakaway points and the imaginary axis crossing points, if any

A unity feedback system has an open loop transfer function, $$G\left( s \right) = {K \over {{s^2}}}.$$ The root locus plot is

When a program is being executed in an $$8085$$ microprocessor, its Program Counter contains

The logic circuit used to generate the active low chip select $$(CS)$$ by an $$8085$$ microprocessor to address a peripheral is shown in Fig. The peripheral will respond to addresses in the range.

The ripple counter shown in Fig. is made up negative edge triggered $$J$$-$$E$$ flips flops. The signal levels at $$J$$ and $$K$$ inputs of all the flip-flops are maintained at logic $$1$$. Assume that all outputs are cleared just prior to applying the clock signal.

$$(a)$$ Create a table of $${Q_0},{Q_1},{Q_2}$$ and $$A$$ in the format given below for $$10$$ successive
$$\,\,\,\,\,\,\,\,$$ input cycles of the clock $$CLK1.$$
$$(b)$$ Determine the module number of the counter.
$$(c)$$ Modify the circuit of Fig. to create a modulo$$-6$$ counter using the same
$$\,\,\,\,\,\,\,$$ components used in the figure.

The frequency of the clock signal applied to the rising edge triggered $$D$$ flip-flop shown in Fig. is $$10$$ $$kHz.$$ The frequency of the signal available at $$Q$$ is

For the circuit shown in Fig. the Boolean expression for the output $$Y$$ in terms of inputs $$P,$$ $$Q,$$ $$R$$ and $$S$$ is

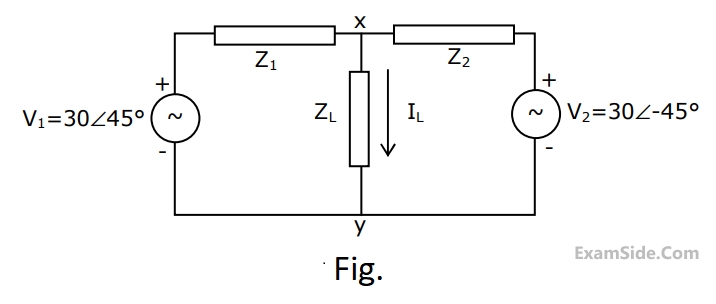
An electrical network is fed by two $$ac$$ sources, as shown in Fig. Given that
$${Z_1} = \left( {1 - j} \right)\Omega ,\,\,{Z_2} = \left( {1 + j} \right)\Omega $$ and $${Z_L} = \left( {1 + j0} \right)\Omega .$$ Obtain the Thevenin equivalent circuit (Thevenin voltage and impedance) across terminals $$X$$ and $$Y$$, and determine the current $${{\rm I}_L}$$ through the load $${Z_L}.$$

The graph of an electrical network has $$N$$ nodes and $$B$$ branches. The number of links, $$L$$, with respect to the choice of a tree, is given by

In the resistor network shown in Fig. all resistor values are $$1\,\,\Omega .$$ $$A$$ current of $$1A$$ passes from terminal $$a$$ to terminal $$b,$$ as shown in the figure. Calculate the voltage between terminals $$a$$ and $$b.$$ [Hint: You may exploit the symmetry of the circuit].

Consider the circuit shown in Fig. If the frequency of the source is $$50$$ $$Hz,$$ then a value of $${t_0}$$ which results in a transient free response is

A two $$-$$ port network, shown in Fig. is described by the following equations:
$$\eqalign{ & {{\rm I}_1} = {Y_{11}}\,\,{E_1} + {Y_{12}}\,\,{E_2} \cr & {{\rm I}_2} = {Y_{21}}\,\,{E_1} + {Y_{22}}\,\,{E_2} \cr} $$

The admittance parameters, $${Y_{11}},\,\,{Y_{12}},\,\,{Y_{21}}$$ and $${Y_{22}}$$ for the network shown are

A first order, low pass filter is given with $$R = 50\,\,\Omega $$ and $$C$$ $$ = 5\mu F.$$ What is the frequency at which the gain of the voltage transfer function of the filter is $$0.25?$$

In the circuit shown in Fig. it is found that the input $$ac$$ voltage $$\left( {{V_i}} \right)$$ and current $$i$$ are in phase. The coupling coefficient is $$K = {M \over {\sqrt {{L_1}{L_2}} }},$$ where $$M$$ is the mutual inductance between the two coils. The value of $$K$$ and the dot polarity of the coil $$P-Q$$ are

A series $$R-L-C$$ circuit has $$R = 50\Omega ;$$ $$L=100$$ $$\mu H$$ and $$C = 1\,\,\mu F.$$ The lower half power frequency of the circuit is

In the circuit shown in Fig. what value of $$C$$ will cause a unity power factor at the $$ac$$ source?

A constant current source is supplying $$10A$$ to a circuit shown in Fig. the switch $$S,$$ which is initially closed for a sufficiently long time, is suddenly opened. Obtain the differential equation governing the behaviour of the inductor current and hence obtain the complete time response of the inductor current. What is the energy stored in $$L,$$ a long time after the switch is opened?

An $$11$$ $$V$$ pulse of $$10$$ $$µ$$s duration is applied to the circuit shown in Fig. Assuming that the capacitor is completely discharged prior to applying the pulse, the peak value of the capacitor voltage is

Kelvin double bridge is best suited for the measurement of

Two in-phase, 50Hz sinusoidal waveform of unit amplitude are fed into channel-1. and channel-2 respectively of an oscilloscope, Assuming that the voltage scale, time scale and other settings are exactly the same for both the channels. What would be observed if the oscilloscope is operated in x-y mode?

The line to line input voltage to the $$3$$ phase, $$50$$ Hz, ac circuit shown in fig is $$100$$ $$V$$ $$r.m.s$$ Assuming that the phase sequence is $$RYB$$ the wattmeter would read.

A $$415$$ $$V,$$ $$2$$ pole, $$3$$ phase, $$50$$ $$Hz,$$ star connected, non-salient pole synchronous motor has synchronous reactance of $$2\,\Omega $$ per phase and negligible stator resistance. At a particular field excitation, it draws 20 A at unity power factor from a $$415$$ $$V,$$ $$3$$ phase, $$50$$ $$Hz$$ supply. The mechanical load on the motor is now increased till the stator current is equal to $$50$$ $$A.$$ The field excitation remains unchanged. Determine:
$$(a)$$ the per phase open circuit voltage $${E_0}$$
$$(b)$$ the developed power for the new operating condition and corresponding power factor.

The flux per pole in a synchronous motor with the field circuit ON and the stator disconnected from the supply is found to be $$25$$ $$mWb.$$ When the stator is connected to the rated supply with the field excitation unchanged, the flux per pole in the achine is found to be $$20$$ $$mWb$$ while the motor is running on no load. Assuming no load losses to be zero, the no load current down by the motor from the supply

A single phase $$6300$$ $$kVA,$$ $$50$$ $$Hz,$$ $$3300V/400V$$ distribution transformer is connected between two $$50$$ $$Hz$$ supply systems, $$A$$ and $$B$$ as shown in Fig. The transformer has $$12$$ and $$99$$ turns in the low and high voltage windings respectively. The magnetizing reactance of the transformer referred to the high voltage side is $$500\Omega .$$ The leakage reactance of the high and low voltage windings are $$1.0\Omega $$ and $$0.012\Omega $$ respectively. Neglect the winding resistance and core losses of the transformer. The Thevenin voltage of system $$A$$ is $$3300V$$ while that of system $$B$$ is $$400V.$$ the short circuit reactance of systems $$A$$ and $$B$$ are $$0.5\Omega $$ and $$0.010\Omega $$ respectively. If no power is transferred between $$A$$ and $$B,$$ so that the two system voltages are in phase, find the magnetizing ampere turns of the transformer.

In a single phase $$3$$ winding transformer the turns ratio for primary: secondary: tertiary windings is $$20:4:1.$$ With the lagging currents of $$50A$$ at a power factor of $$0.6$$ in the tertiary winding find the primary current and power factor.

A $$230V,$$ $$250$$ $$rpm.$$ $$100A$$ separately excited $$dc$$ motor has an armature resistance of $$0.5\,\Omega .$$ The motor is connected to $$230V$$ $$dc$$ supply and rated $$dc$$ voltage is applied to the field winding. It is driving a load whose torque speed characteristic is given by $${T_L} = 500$$$$ - 10\omega ,$$ where $$\omega $$ is the rotational speed expressed in $$rad/sec$$ and $${T_L}$$ is the load torque in $$Nm.$$ Find the steady state speed at which the motor will drive the load and the armature current drawn by it from the source. Neglect the rotational losses of the machine.

If a 400 V, 50 Hz, star connected, 3 phase squirrel cage induction motor is operated from a 400 V, 75 Hz supply, the torque that the motor can now provide while drawing rated current from the supply?

A 400V/200V/200V, 50 Hz three winding transformer is connected as shown in Figure. The reading of the voltmeter 'V' will be

A 1 kVA, 230V/100V, single phase, 50 Hz transformer having negligible winding resistance and leakage inductance is operating under saturation, while 250 V, 50 Hz sinusoidal supply is connected to the high voltage winding. A resistive load is connected to the low voltage winding which draws rated current. Which one of the following quantities will not be sinusoidal?

A 200 V, 2000 rpm, 10A, separately excited d.c. motor has an armature resistance of 2 $$\Omega$$. Rated d.c. voltage is applied to both the armature and field winding of the motor. If the armature drawn 5A from the source, the torque developed by the motor is

A dc series motor fed from rated supply voltage is overloaded and its magnetic circuit is saturated. The torque-speed characteristic of this motor will be approximately represented by which curve of Fig.

Given a vector field $$\overrightarrow F ,$$ the divergence theorem states that

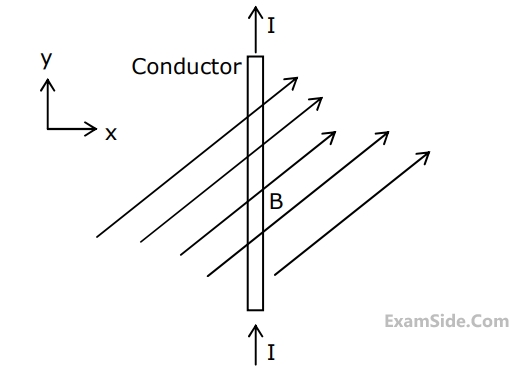
The magnetic vector potential in a region is defined by $$\overrightarrow A = {e^{ - y}}\sin \left( x \right){\widehat a_z}.$$ An infinitely long conductor, having a cross section area, $$a=5$$ $$m{m^2}$$ and carrying a $$dc$$ current, $${\rm I} = 5\,A$$ in the $$Y$$ direction, passes through this region as shown in Fig. Determine the expression for $$(a)$$ $$\overrightarrow B $$ and $$(b)$$ force density $$\overrightarrow f $$ exerted on the conductor

Let $$Y(s)$$ be the Laplace transform of function $$y(t),$$ then the final value of the function is __________.

Given a vector field $${\overrightarrow F ,}$$ the divergence theorem states that

The determinant of the matrix $$\left[ {\matrix{ 1 & 0 & 0 & 0 \cr {100} & 1 & 0 & 0 \cr {100} & {200} & 1 & 0 \cr {100} & {200} & {300} & 1 \cr } } \right]$$ is

Fig. $$(a)$$ shows an inverter circuit with a $$dc$$ source voltage $${V_{s}}$$. The semiconductor switches of the inverter are operated in such a manner that the pole voltages $${V_{10}}$$ and $${V_{20}}$$ are as shown in fig.
Fig. $$(b).$$ What is the rms value of the pole-to-pole voltage $${V_{12}}$$:

In the chopper circuit shown in fig the input $$dc$$ voltage has a constant value $${{V_s}}$$. the output voltage $${{V_0}}$$ is assumed ripple free. The switch $$S$$ is operated with a switching time period $$T$$ and a duty ratio $$D.$$ What is the value of $$D$$ at the boundary of continuous and discontinuous conduction of the inductor current $${i_L}$$?

A step down chopper is operated in the continuous conduction mode in steady state with a constant duty ratio $$D.$$ If $${V_0}$$ is the magnitude of the $$dc$$ output voltage and if $${V_s}$$ is the magnitude of the $$dc$$ input voltage, the ratio $${{{V_0}} \over {{V_s}}}$$ is given by

In the single phase diode bridge rectifier shown in fig, the load resistor is
$$R = 50\Omega .$$ The source voltage is
$$V = 200sin\omega t,$$
Where $$\omega = 2\pi \times 50$$ radians per second. The power dissipated in the load resistor $$R$$ is

A three phase thyristor bridge rectifier is used in a $$HVDC$$ link. The firing angle $$\alpha $$ (as measured from the point of natural commutation) is constrained to lie between $${5^ \circ }$$ and $${30^ \circ }$$. If the $$dc$$ side current and $$ac$$ side voltage magnitude are constant, which of the following statements is true (neglect harmonics in the $$ac$$ side current and commutation overlap in your analysis)

A six pulse thyristor rectifier bridge is connected to a balanced $$50Hz$$ three phase $$ac$$ source. Assuming that the $$dc$$ output current of the rectifier is constant, the lowest frequency harmonic component in the $$ac$$ source line current is

A long wire composed of a smooth round conductor runs above and parallel to the ground (assumed to be a large conducting plane). A high voltage exists between the conductor and the ground. The maximum electric stress occurs at

Two transposed $$3$$ phase lines run parallel to each other. The equation describing the voltage drop in both lines is given below.

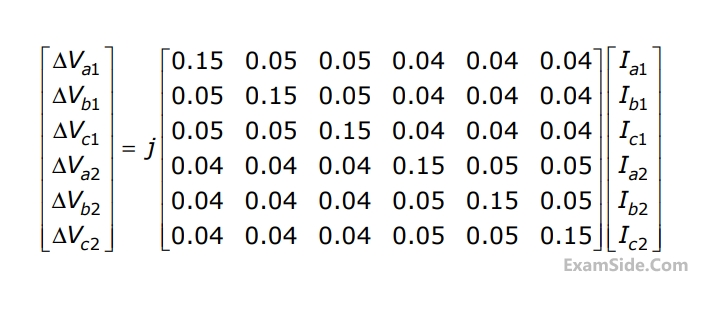
Compute the self and mutual zero sequence impedances of this system i.e, compute $${Z_{011}},\,\,{Z_{012}},\,\,{Z_{021}},\,\,{Z_{022}}\,\,\,$$ in the following equations.
$$\Delta {V_{01}} = {Z_{011}}\,{{\rm I}_{01}} + {Z_{012}}\,{{\rm I}_{02}}$$
$$\Delta {V_{02}} = {Z_{021}}\,{{\rm I}_{01}} + {Z_{022}}\,{{\rm I}_{02}}\,\,$$ where $$\,\Delta {V_{01}},$$
$$\Delta {V_{02}},\,{{\rm I}_{01}},\,{{\rm I}_{02}}\,\,$$ are the zero sequence voltage drops and currents for the two lines respectively.

A power system consists of 2 areas (Area 1 and Area 2) connected by a single tie line (figure). It is required to carry out a load flow study on this system. While entering the network data, the tie-line data (connectivity and parameters) is inadvertently left out. If the load flow program is run with this incomplete data.

Consider a power system with three identical generators. The transmission losses are negligible. One generator ($$G1$$) has a speed governor which maintains its speed constant at the rated value, while the other generators ($$G2$$ and $$G3$$) have governors with a droop of $$5$$%. If the load of the system is increased, then in steady state.

Consider the problem of relay co-ordination for the distance relays $$R1$$ and $$R2$$ on adjacent lines of a transmission system figure. The Zone $$1$$
and Zone $$2$$ settings for both the relays are indicated on the diagram. Which of the following indicates the correct time setting for the Zone $$2$$ of relays $$R1$$ and $$R2.$$

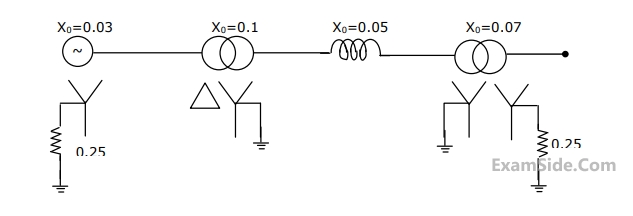
A generator is connected to a transformer which feeds another transformer through a short feeder. The zero sequence impedance values are expressed in pu on a common base and are indicated in figure. The Thevenin equivalent zero sequence impedance at point B is

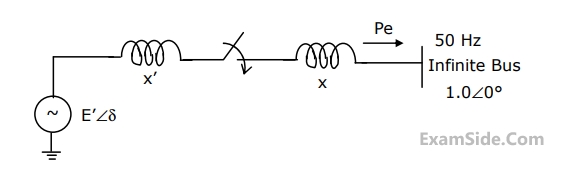
A synchronous generator is to be connected to an infinite bus through a transmission line of reactance X = 0.2 pu, as shown in figure the generator data is as follows:

X¹ = 0.1 pu, E¹ = 1.0 pu, H = 5 MJ/MVA, mechanical power P_m = 0.0 pu, $$\omega $$_B = 2 $$\pi \times $$50 rad/sec. All quantities are expressed on a common base.

The generator is initially running on open circuit with the frequency of the open circuit voltage slightly higher than that of the infinite bus. If at the instant of switch closure $$\delta = 0$$ and $$\omega = {{d\delta } \over {dt}} = {\omega _{init}},$$ compute the maximum value of $${\omega _{init}}$$ so that the generator pulls into synchronism.

$$\int {\left( {{{2H} \over {{\omega _B}}}} \right)\omega d\omega + {P_e}d\delta = 0} $$

A transmission line has a total series reactance of 0.2 pu. Reactive power compensation is applied at the midpoint of the line and it is controlled such that the midpoint voltage of the transmission line is always maintained at 0.98 pu. If voltage at both ends of the line are maintained at 1.0 pu, then the steady state power transfer limit of the transmission line is

A long lossless transmission line has a unity power factor (UPF) load at the receiving end and an ac voltage source at the sending end. The parameters of the transmission line are as follows:
Characteristic impedance $${Z_c} = 400\Omega ,\,\,$$, propagation constant $$\,\beta = 1.2 \times {10^{ - 3}}\,\,rad/km,\,\,$$ and length $$\,l = 100\,km.\,\,$$ The equation relating sending and receiving end questions is $${V_s} = {V_r}\,\cosh \,\,\left( {\beta l} \right) + j\,Z{}_c\,\,\sinh \left( {\beta l} \right){{\rm I}_R}$$ Complete the maximum power that can be transferred to the UPF load at the receiving end if $$\left| {{V_s}} \right| = 230\,\,kV.\,\,$$

Consider a long, two-wire line composed of solid round conductors. The radius of both conductors is $$0.25$$ cm and the distance between their centers is $$1$$m. If this distance is doubled, then the inductance per unit length.

A single input single output system with $$y$$ as output and $$u$$ as input, is described by $$${{{d^2}y} \over {d{t^2}}} + 2{{dy} \over {dt}} + 10y = 5{{d\,u} \over {dt}} - 3\,u$$$
For the above system find an input $$u(t),$$ with zero initial condition, that produces the same output as with no input and with the initial conditions.
$${{d\,y\left( {{0^ - }} \right)} \over {dt}} = - 4,\,\,\,y\left( {{0^ - }} \right) = 1$$

What is the $$rms$$ value of the voltage waveform shown in Fig?

Fourier Series for the waveform, $$f(t)$$ shown in Fig. is

$$s(t)$$ is step response and $$h(t)$$ is impulse response of a system. Its response $$y(t)$$ for any input $$u(t)$$ is given by

Let Y(s) be the Laplace transformation of the function y(t), then the final value of the function is