for (i = n, j = 0; i > 0; i /= 2, j += i);
let val (j) denote the value stored in the variable j after termination of the for loop. Which one of the following is true?
 Which one of the following cannot be the sequence of edges added, in that order, to a minimum spanning tree using Kruskal’s algorithm?
Which one of the following cannot be the sequence of edges added, in that order, to a minimum spanning tree using Kruskal’s algorithm? A 3-ary max heap is like a binary max heap, but instead of 2 children, nodes have 3 children. A 3-ary heap can be represented by an array as follows: The root is stored in the first location, a[0], nodes in the next level, from left to right, is stored from a[1] to a[3]. The nodes from the second level of the tree from left to right are stored from a[4] location onward. An item x can be inserted into a 3-ary heap containing n items by placing x in the location a[n] and pushing it up the tree to satisfy the heap property.
Suppose the elements 7, 2, 10 and 4 are inserted, in that order, into the valid 3- ary max heap found in the previous question. Which one of the following is the sequence of items in the array representing the resultant heap?
$$T\left( n \right){\rm{ }} = {\rm{ 2T(}}\left\lceil {\sqrt n } \right\rceil {\rm{) + }}\,{\rm{1 T(1) = 1}}$$
Which one of the following is true?
A 3-ary max heap is like a binary max heap, but instead of 2 children, nodes have 3 children. A 3-ary heap can be represented by an array as follows: The root is stored in the first location, a[0], nodes in the next level, from left to right, is stored from a[1] to a[3]. The nodes from the second level of the tree from left to right are stored from a[4] location onward. An item x can be inserted into a 3-ary heap containing n items by placing x in the location a[n] and pushing it up the tree to satisfy the heap property.
Which one of the following is a valid sequence of elements in an array representing 3-ary max heap?
Which one of the following grammars generates the following language?
$$L = \left( {{a^i}{b^j}|i \ne j} \right)$$Consider the following grammar.
$$\eqalign{ & S \to S*E \cr & S \to E \cr & E \to F + E \cr & E \to F \cr & F \to id \cr} $$Consider the following LR(0) items corresponding to the grammar above.
$$\eqalign{ & (i)\,S \to S*.E \cr & (ii)\,E \to F. + E \cr & (iii)\,E \to F + .E \cr} $$Given the items above, which two of them will appear in the same set in the canonical sets-of-items for the grammar?
for (i = 0; i < n; i++)
{
for (j=0; j < n; j++)
{
if (i%2)
{
x += (4*j + 5*i);
y += (7 + 4*j);
}
}
} Consider the following translation scheme.
$$\eqalign{ & S \to ER \cr & R \to *E\left\{ {pr{\mathop{\rm int}} ('*');} \right\}R\,|\,\varepsilon \cr & E \to F + E\left\{ {pr{\mathop{\rm int}} (' + ');} \right\}\,|\,F \cr & F \to S\,|\,id\,\left\{ {pr{\mathop{\rm int}} (id.value);} \right\} \cr} $$Here id is a token that represents an integer and id.value represents the corresponding integer value. For an input '2 * 3 + 4' this translation scheme prints
Consider the following grammar:
$$\eqalign{ & S \to FR \cr & R \to *S\,|\,\varepsilon \cr & F \to id \cr} $$In the predictive parser table, M, of the grammar the entries $$M\left[ {S,id} \right]$$ and $$M\left[ {R,\$ } \right]$$ respectively.
 For the given connection of LANs by bridges, which one of the following choices represents the depth-first traversal of the spanning tree of bridges?
For the given connection of LANs by bridges, which one of the following choices represents the depth-first traversal of the spanning tree of bridges? Consider the correct spanning tree for the previous question. Let host H1 send out a broadcast ping packet. Which of the following options represents the correct forwarding table on B3?
Consider the correct spanning tree for the previous question. Let host H1 send out a broadcast ping packet. Which of the following options represents the correct forwarding table on B3?
Assume that the content of memory location $$3000$$ is $$10$$ and the content of the register $$R3$$ is $$2000$$. The content of each of the memory locations from $$2000$$ to $$2010$$ is $$100.$$ The program is loaded from the memory location $$1000.$$ All the numbers are in decimal.
Assume that the memory is word addressable. The number of memory references for accessing the data in executing the program completely is

Assume that the content of memory location $$3000$$ is $$10$$ and the content of the register $$R3$$ is $$2000$$. The content of each of the memory locations from $$2000$$ to $$2010$$ is $$100.$$ The program is loaded from the memory location $$1000.$$ All the numbers are in decimal.
Assume that the memory is word addressable. After the execution of this program, the content of memory location $$2010$$ is

Assume that the content of memory location $$3000$$ is $$10$$ and the content of the register $$R3$$ is $$2000$$. The content of each of the memory locations from $$2000$$ to $$2010$$ is $$100.$$ The program is loaded from the memory location $$1000.$$ All the numbers are in decimal.
Assume that the memory is byte addressable and the word size is $$32$$ bits. If an interrupt occurs during the execution of the instruction $$''INC$$ $$R3'',$$ what return address will be pushed on to the stack?
The value of $${h_2}$$ is
The value of $${h_1}$$ is
d(P) = 5 units f(P) = 12 units
d(Q) = 6 units f(Q) = 10 units
d(R) = 14 unit f(R) = 18 units
Which one of the following statements is TRUE about the graph
int func(int m, int n)
{
if (E) return 1;
else return(func(m -1, n) + func(m - 1, n - 1));
} void insert(Q, X){
push(S1, X);
}
void delete(Q){
if(stack - empty(S1)) then {
print("Q is empty");
return;
}else while (!(stack - empty(S1))){
X = pop(S1);
push(S2, X);
}
X = pop(S2);
}I) Relational algebra
II) Tuple relational calculus restricted to safe expressions
III) Domain relational calculus restricted to safe expressions
Consider a database with three relation instances shown below. The primary keys for the Drivers and Cars relation are Did and cid respectively and the records are stored in ascending order of these primary keys as given in the tables. No indexing is available in the database.
D: Drivers Relation
| Did | Dname | rating | Age |
|---|---|---|---|
| 22 | Karthikeyan | 7 | 25 |
| 29 | Salman | 1 | 33 |
| 31 | Boris | 8 | 55 |
| 32 | Amoldt | 8 | 25 |
| 58 | Schumacher | 10 | 35 |
| 64 | Sachin | 7 | 35 |
| 71 | Senna | 10 | 16 |
| 74 | Sachin | 9 | 35 |
| 85 | Rahul | 3 | 25 |
| 95 | Ralph | 3 | 53 |
R: Reserves Relation
| Did | cid | Day |
|---|---|---|
| 22 | 101 | 10/10/06 |
| 22 | 102 | 10/10/06 |
| 22 | 103 | 8/10/06 |
| 22 | 104 | 7/10/06 |
| 31 | 102 | 10/11/06 |
| 31 | 103 | 6/11/06 |
| 31 | 104 | 12/11/06 |
| 64 | 101 | 5/9/06 |
| 64 | 102 | 8/9/06 |
| 74 | 103 | 8/9/06 |
C: Cars relation
| cid | Cname | Color |
|---|---|---|
| 101 | Renault |
Blue |
| 102 | Renault |
Red |
| 103 | Ferrari | Green |
| 104 | Jaguar | Red |
What is the output of the following SQL query?
Select D.dname
From Drivers D
Where D.did in (SELECT R.did
From Cars C,Reserves R
WHERE R.cid = C.cid and C.color = 'green')Consider a database with three relation instances shown below. The primary keys for the Drivers and Cars relation are Did and cid respectively and the records are stored in ascending order of these primary keys as given in the tables. No indexing is available in the database.
D: Drivers Relation
| Did | Dname | rating | Age |
|---|---|---|---|
| 22 | Karthikeyan | 7 | 25 |
| 29 | Salman | 1 | 33 |
| 31 | Boris | 8 | 55 |
| 32 | Amoldt | 8 | 25 |
| 58 | Schumacher | 10 | 35 |
| 64 | Sachin | 7 | 35 |
| 71 | Senna | 10 | 16 |
| 74 | Sachin | 9 | 35 |
| 85 | Rahul | 3 | 25 |
| 95 | Ralph | 3 | 53 |
R: Reserves Relation
| Did | cid | Day |
|---|---|---|
| 22 | 101 | 10/10/06 |
| 22 | 102 | 10/10/06 |
| 22 | 103 | 8/10/06 |
| 22 | 104 | 7/10/06 |
| 31 | 102 | 10/11/06 |
| 31 | 103 | 6/11/06 |
| 31 | 104 | 12/11/06 |
| 64 | 101 | 5/9/06 |
| 64 | 102 | 8/9/06 |
| 74 | 103 | 8/9/06 |
C: Cars relation
| cid | Cname | Color |
|---|---|---|
| 101 | Renault |
Blue |
| 102 | Renault |
Red |
| 103 | Ferrari | Green |
| 104 | Jaguar | Red |
Select D.dname
From Drivers D
Where D.did in (SELECT R.did
From Cars C,Reserves R
WHERE R.cid = C.cid and C.color = 'green')Let n be the number of comparisons performed when the above SQL query is optimally executed. If linear search is used to locate a tuple in a relation using primary key, then n lies in the range
Consider the relation "enrolled (student, course)" in which (student, course) is the primary key, and the relation "paid (student, amount)" where student is the primary key. Assume no null values and no foreign keys or integrity constraints. Given the following four queries:
Query 1:
Select student
from enrolled
where student in (select student from paid)Query 2:
Select student
from paid
where student in (select student from enrolled)Query 3:
Select E.student
from enrolled E, paid P
where E.student = P.studentQuery 4:
Select student
from paid
where exists (Select *
from enrolled
where enrolled.student = paid.student)Which one of the following statements is correct?
Query1:
Select A.customer, count(B.customer)
From account A, account B
Where A.balance <=B.balance
Group by A.customer
Query2:
Select A.customer, 1+count(B.customer)
From account A, account B
Where A.balance < B.balance
Group by A.customerConsider these statements about Query1 and Query2.
1. Query1 will produce the same row set as Query2 for some but not all databases.
2. Both Query1 and Query2 are correct implementation of the specification
3. Query1 is a correct implementation of the specification but Query2 is not
4. Neither Query1 nor Query2 is a correct implementation of the specification
5. Assigning rank with a pure relational query takes less time than scanning in decreasing balance order assigning ranks using ODBC.
Which two of the above statements are correct?$$\eqalign{ & AB \to CD,\,AF \to D,\,\,DE \to F, \cr & C \to G.\,\,\,\,\,\,\,\,\,\,F \to E.\,\,\,\,\,\,\,\,\,G \to A. \cr} $$
Which one of the following options is false?


A disk seek takes $$4ms$$, disk data transfer bandwidth is $$300MB/s$$ and checking a tuple to see if amount is greater than $$x$$ takes $$10\mu s.$$ Which of the following statements is correct?
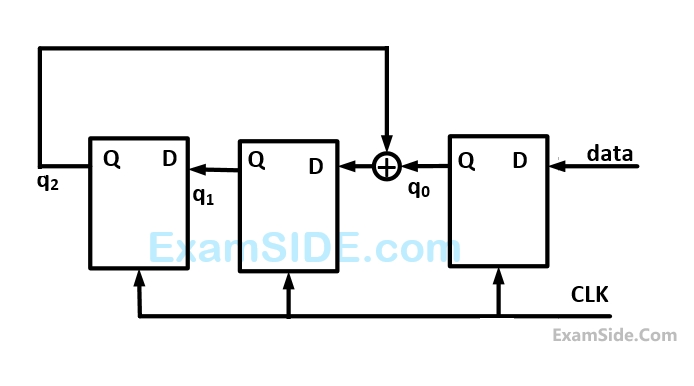
The following data: $$100110000$$ is supplied to the ''data'' terminal in nine clock cycles. After that the values of $${q_2}{q_1}{q_0}$$ are

Which one of the following statements is false?
The maximum degree of a vertex in $$G$$ is
the number of vertices of degree zero in $$G$$ is
$$X = $$ {$$n\left| {1 \le n \le 123,\,\,\,\,\,n} \right.$$ is not divisible by either $$2, 3$$ or $$5$$ }
Then $$\sum\limits_{i - 1}^m {f\,(i)} $$ is
$${\rm I}$$) $$\,\,\,\,\,\,f\left( {x,y} \right) = x + y - 3$$
$${\rm I}{\rm I}$$ $$\,\,\,\,\,\,f\left( {x,y} \right) = {\mkern 1mu} \max \left( {x,y} \right)$$
$${\rm I}{\rm I}{\rm I}$$$$\,\,\,\,\,f\left( {x,y} \right) = \,{x^y}$$
Which one of them is false?
Let $$X = \,\left( {E\, \cap \,F\,} \right)\, - \,\left( {F\, \cap \,G\,} \right)$$
and $$Y = \,\left( {E\, - \left( {E\, \cap \,G} \right)} \right)\, - \,\left( {E\, - \,F\,} \right)$$. Which one of the following is true?
($${\rm I}$$) $$P\Delta \left( {Q \cap R} \right) = \left( {P\Delta Q} \right) \cap \left( {P\Delta R} \right)$$
($${\rm I}{\rm I}$$) $$P \cap \left( {Q\Delta R} \right) = \left( {P \cap Q} \right)\Delta \left( {P \cap R} \right)$$
$$\forall x\forall y\left( {R\left( {x,\,y} \right) \Rightarrow R\left( {y,x} \right)} \right).$$
The formula is

Let ~ be the unary negation (NOT) operator, with higher precedence then $$ \odot $$. Which one of the following is equivalent to $$A \wedge B?$$
$${\rm P}1:\,\,\left( {\left( {A \wedge B} \right) \to C} \right) \equiv \left( {\left( {A \to C} \right) \wedge \left( {B \to C} \right)} \right)$$
$${\rm P}2:\,\,\left( {\left( {A \vee B} \right) \to C} \right) \equiv \left( {\left( {A \to C} \right) \vee \left( {B \to C} \right)} \right)$$ Which one of the following is true?
Tigers and lion attack if they are hungry of threatened.
void barrier (void) {
1: P(S);
2: process_arrived++;
3: V(S);
4: while (process_arrived !=3);
5: P(S);
6: process_left++;
7: if (process_left==3) {
8: process_arrived = 0;
9: process_left = 0;
10: }
11: V(S);
}
Which one of the following rectifies the problem in the implementation?
void P (binary_semaphore *s) {
unsigned y;
unsigned *x = &(s->value);
do {
fetch-and-set x, y;
} while (y);
}
void V (binary_semaphore *s) {
S->value = 0;
} void barrier (void) {
1: P(S);
2: process_arrived++;
3: V(S);
4: while (process_arrived !=3);
5: P(S);
6: process_left++;
7: if (process_left==3) {
8: process_arrived = 0;
9: process_left = 0;
10: }
11: V(S);
}
The above implementation of barrier is incorrect. Which one of the following is true?
void swap(int *px, int *py)
{
*px = *px - *py;
*py = *px + *py;
*px = *py - *px;
}S2: may generate a segmentation fault at runtime depending on the arguments passed
S3: correctly implements the swap procedure for all input pointers referring to integers stored in memory locations accessible to the process
S4: implements the swap procedure correctly for some but not all valid input pointers
S5: may add or subtract integers and pointers.
Let $$L = \left\{ {s \in {{\left( {0 + 1} \right)}^ * }\left| {\,d\left( s \right)\,} \right.} \right.$$ mod $$5=2$$ and $$d(s)$$ mod $$\left. {7 \ne 4} \right\}$$
Which of the following statement is true?
$$G = \left\{ {S \to SS,\,S \to ab,\,S \to ba,\,S \to \varepsilon } \right\}$$
$$1.$$ $$G$$ is ambiguous
$$2.$$ $$G$$ produces all strings with equal number of $$a's$$ and $$b's$$
$$3.$$ $$G$$ can be accepted by a deterministic $$PDA$$.
Which combination below expresses all the true statements about $$G?$$
$$\,\,\,{L_2} = \left\{ {{0^{n + m}}{1^{n + m}}{0^m}\left| {n,m \ge 0} \right.} \right\},$$ and
$$\,\,\,\,{L_3} = \left\{ {{0^{n + m}}{1^{n + m}}{0^{n + m}}\left| {n,m \ge 0} \right.} \right\},$$ Which of these languages are NOT context free?