$$\sum\limits_{1 \le k \le n} {O(n)} $$ where O(n) stands for order n is:

The proposition $$p \wedge \left( { \sim p \vee q} \right)$$ is

The value of the double integral $$\int\limits_0^1 {\int\limits_x^{{1 \over x}} {{x \over {1 + {y^2}}}\,\,dx\,\,dy = \_\_\_\_\_.} } $$

The eigen vector (s) of the matrix
$$\left[ {\matrix{ 0 & 0 & \alpha \cr 0 & 0 & 0 \cr 0 & 0 & 0 \cr } } \right],\alpha \ne 0$$ is (are)

If $$A = \left[ {\matrix{ 1 & 0 & 0 & 1 \cr 0 & { - 1} & 0 & { - 1} \cr 0 & 0 & i & i \cr 0 & 0 & 0 & { - i} \cr } } \right]$$ the matrix $${A^4},$$
calculated by the use of Cayley - Hamilton theoram (or) otherwise is

Let $${\rm A}$$ be a finite set of size $$n$$. The number of elements in the power set of $${\rm A} \times {\rm A}$$ is

Let $$S$$ be an infinite set and $${S_1},\,\,{S_2},....\,\,{S_n}$$ be sets such that $${S_1} \cup {S_2} \cup ....... \cup {S_n} = S$$. Then

Show that proposition $$C$$ is a logical consequence of the formula $$A \wedge \left( {A \to \left( {B \vee C} \right) \wedge \left( {B \to \sim A} \right)} \right)$$ using truth tables.

Assume that the following jobs are to be executed on a single processor system.

Job Id	CPU Burst Time
p	4
q	1
r	8
s	1
t	2

The jobs are assumed to have arrived at time $${0^ + }$$ and in the order $$p,q,r,s,t.$$ Calculate the departure time (completion time) for job $$p$$ if scheduling is round robin with time slice$$1.$$

Consider a system having m resources of the same type. These resources are shared by 3 processes A, B and C, which have peak demands of 3, 4 and 6 respectively. For what value of m deadlock will not occur?

A certain moving arm disk storage, with one head, has the following specifications.
Number of track/recording
Surface $$=200$$
Disk rotation speed $$=2400$$$$rpm$$
Track storage capacity $$=62,500$$ $$bits$$
The average latency of this device is
$$P$$ $$msec$$ and the data transfer rate is
$$Q$$ $$bits / sec.$$ Write the value of $$P$$&$$Q$$

The root directory of a disk should be placed:

The following page addresses, in the given sequence, were generated by a program:
1 2 3 4 1 3 5 2 1 5 4 3 2 3

This program is run on a demand paged virtual memory system, with main memory size equal to $$4$$ pages. Indicate the page references for which page faults occurs for the following page replacement algorithms.
(a) $$LRU$$
(b) $$FIFO$$

Assume that the main memory is empty initially.

A simple two-pass assembler does the following in the first pass:

A part of the system software, which under all circumstances must reside in the main memory is:

The details of an interrupt cycle are shown in Figure
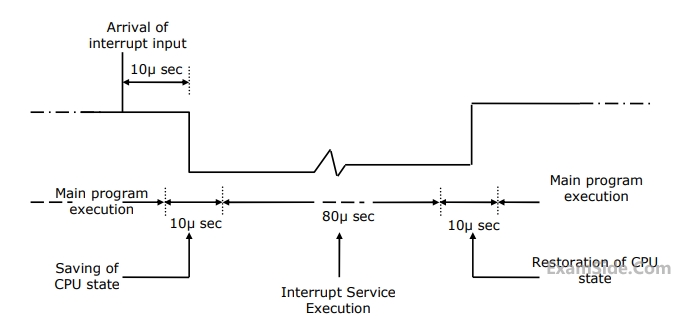
Given that an interrupt input arrives every $$1$$ $$msec,$$ what is the percentage of the total time that the $$CPU$$ devotes for the main program execution.

What does the following code do?

var a, b : integer;
begin
    a:=a+b;
    b:=a-b;
    a:=a-b;
end;