Signals and Systems
1
GATE ECE 2011
MCQ (Single Correct Answer)
+2
-0.6
Two system $${H_1}\left( z \right)$$ and $${H_2}\left( z \right)$$ are connected in cascade as shown below. The overall output $$y\left( n \right)$$ is the same as the input $$x\left( n \right)$$ with a one unit delay. The transfer function of the second system $${H_2}\left( z \right)$$ is
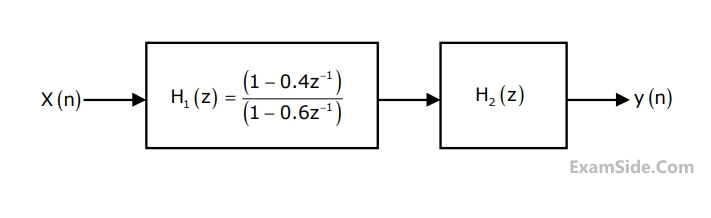

2
GATE ECE 2010
MCQ (Single Correct Answer)
+2
-0.6
The transfer function of a discrete time LTI system is given by
$$H\left( z \right) = {{2 - {3 \over 4}{z^{ - 1}}} \over {1 - {3 \over 4}{z^{ - 1}} + {1 \over 8}{z^{ - 2}}}}$$
$$H\left( z \right) = {{2 - {3 \over 4}{z^{ - 1}}} \over {1 - {3 \over 4}{z^{ - 1}} + {1 \over 8}{z^{ - 2}}}}$$
Consider the following statements:
S1: The system is stable and causal for $$ROC:\,\,\,\left| z \right| > \,1/2$$
S2: The system is stable but not causal for $$ROC:\,\,\,\left| z \right| < \,1/4$$
S3: The system is neither stable nor causal for $$ROC:\,\,1/4\, < \,\left| z \right| < \,{\raise0.5ex\hbox{$\scriptstyle 1$}
\kern-0.1em/\kern-0.15em
\lower0.25ex\hbox{$\scriptstyle 2$}}$$
Which one of the following statements is valid?
3
GATE ECE 2008
MCQ (Single Correct Answer)
+2
-0.6
A discrete time linear shift - invariant system has an impulse response $$h\left[ n \right]$$ with $$h\left[ 0 \right]$$ $$ = 1,\,\,h\left[ 1 \right]\,\, = - 1,\,\,h\left[ 2 \right]\,\, = \,2$$, and zero otherwise. The system is given an input sequence $$x\left[ n \right]$$ with $$x\left[ 0 \right]$$ $$ = \,x\left[ 2 \right]\, = \,1,$$ and zero otherwise. The number of nonzero samples in the output sequence $$y\left[ n \right]$$, and the value of $$y\left[ 2 \right]$$ are, respectively
4
GATE ECE 2006
MCQ (Single Correct Answer)
+2
-0.6
A system with input $$x\left( n \right)$$ and output $$y\left( n \right)$$ is given as $$y\left( n \right)$$ $$ = \left( {\sin {5 \over 6}\,\pi \,n} \right)x\left( n \right).$$ The system is
GATE ECE Subjects
Signals and Systems
Network Theory
Control Systems
Digital Circuits
General Aptitude
Electronic Devices and VLSI
Analog Circuits
Engineering Mathematics
Microprocessors
Communications
Electromagnetics