ExamSIDE
Questions (Powered by ExamGOAL)
Network Theory
Network Elements
Marks 1Marks 2Marks 5
Network Theorems
Marks 1Marks 2Marks 5
Transient Response
Marks 1Marks 2Marks 3Marks 5Marks 8Marks 10
Sinusoidal Steady State Response
Marks 1Marks 2Marks 5Marks 8
Two Port Networks
Marks 1Marks 2Marks 5Marks 8
Network Graphs
Marks 1Marks 2
State Equations For Networks
Marks 5
Miscellaneous
Marks 2Marks 3Marks 5
Previous Next
1
GATE ECE 2016 Set 3
Numerical
+1
-0
The z-parameter matrix for the two-port network shown is $$$\left[ {\matrix{ {2\,j\,\omega } & {j\,\omega } \cr {j\,\omega } & {3\, + \,2\,j\,\omega } \cr } } \right]$$$ Where the entries are in $$\Omega $$. Suppose $$\,{Z_b}\,\left( {j\,\omega } \right) = {R_b} + j\,\omega $$ 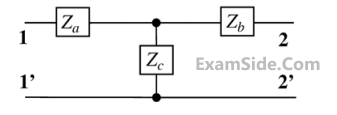GATE ECE 2016 Set 3 Network Theory - Two Port Networks Question 34 English Then the value of $${R_b}$$ (in $$\Omega $$) equals _______________________3
Your input ____
2
GATE ECE 2015 Set 2
MCQ (Single Correct Answer)
+1
-0.3
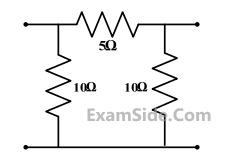
The 2-port admittance matrix of the circuit shown is given by GATE ECE 2015 Set 2 Network Theory - Two Port Networks Question 35 English
A
$$\left[ {\matrix{ {0.3} & { - 0.2} \cr { - 0.2} & {0.3} \cr } } \right]$$
B
$$\left[ {\matrix{ {15} & { 5} \cr { 5} & {15} \cr } } \right]$$
C
$$\left[ {\matrix{ {3.33} & { 5} \cr { 5} & {3.33} \cr } } \right]$$
D
$$\left[ {\matrix{ {0.3} & { 0.4} \cr { 0.4} & {0.3} \cr } } \right]$$
3
GATE ECE 2010
MCQ (Single Correct Answer)
+1
-0.3
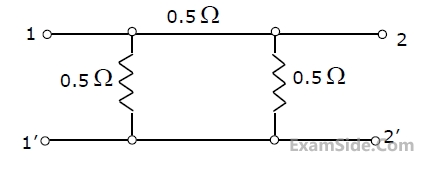
For the two-port network shown below, the short-circuit admittance parameter matrix is GATE ECE 2010 Network Theory - Two Port Networks Question 51 English
A
$$\begin{bmatrix}4&-2\\-2&4\end{bmatrix}S$$
B
$$\begin{bmatrix}1&-0.5\\-0.5&1\end{bmatrix}S$$
C
$$\begin{bmatrix}1&0.5\\0.5&1\end{bmatrix}S$$
D
$$\begin{bmatrix}4&2\\2&4\end{bmatrix}S$$
4
GATE ECE 2009
MCQ (Single Correct Answer)
+1
-0.3
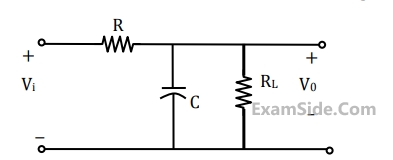
If the transfer function of the following network is $$\,{{{V_0}(s)} \over {{V_i}(s)}} = {1 \over {2\, + \,sCR}}$$ GATE ECE 2009 Network Theory - Two Port Networks Question 36 English

The value of the load resistance $${R_L}$$ is

A
R/4
B
R/2
C
R
D
2R
Previous Next
Questions Asked from Marks 1
GATE ECE 2023 (1) GATE ECE 2018 (1) GATE ECE 2016 Set 1 (1) GATE ECE 2016 Set 3 (1) GATE ECE 2015 Set 2 (1) GATE ECE 2010 (1) GATE ECE 2009 (1) GATE ECE 2005 (1) GATE ECE 2001 (2) GATE ECE 1999 (1) GATE ECE 1998 (1) GATE ECE 1994 (1)
GATE ECE Subjects
Signals and Systems
Network Theory
Control Systems
Digital Circuits
General Aptitude
Electronic Devices and VLSI
Analog Circuits
Engineering Mathematics
Microprocessors
Communications
Electromagnetics