Control Systems
1
GATE EE 2011
MCQ (Single Correct Answer)
+1
-0.3
The steady state error of a unity feedback linear system for a unit step input is $$0.1.$$ The steady state error of the same system, for a pulse input $$r(t)$$ having a magnitude of $$10$$ and a duration of one second, as shown in the figure is
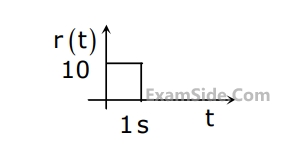

2
GATE EE 2010
MCQ (Single Correct Answer)
+1
-0.3
For the system $${2 \over {\left( {s + 1} \right)}},$$ the approximate time taken for a step response to reach $$98$$% of its final value is
3
GATE EE 2008
MCQ (Single Correct Answer)
+1
-0.3
A function $$y(t)$$ satisfies the following differential equation : $${{dy\left( t \right)} \over {dt}} + y\left( t \right) = \delta \left( t \right)$$
Where $$\delta \left( t \right)$$ is the delta function. Assuming zero initial condition, and denoting the unit step function by $$u(t),y(t)$$ can be of the form
4
GATE EE 2004
MCQ (Single Correct Answer)
+1
-0.3
Consider the function $$F\left( s \right) = {5 \over {s\left( {{s^2} + 3s + 2} \right)}}$$ Where $$F(s)$$ is the Laplace transform of the function $$f(t).$$ The initial value of $$f(t)$$ is equal to
GATE EE Subjects
Electromagnetic Fields
Signals and Systems
Engineering Mathematics
General Aptitude
Power Electronics
Power System Analysis
Analog Electronics
Control Systems
Digital Electronics
Electrical Machines
Electric Circuits
Electrical and Electronics Measurement