1
GATE ECE 2018
Numerical
+2
-0
The contour
C
given below is on the complex plane $$z = x + jy$$, where $$j = \sqrt { - 1} $$.
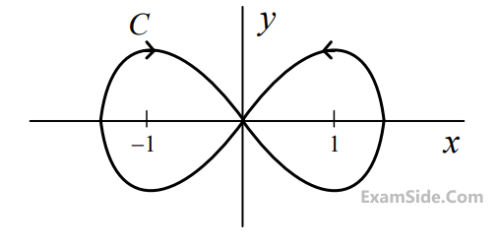 The value of the integral $${1 \over {\pi j}}\oint\limits_C {{{dz} \over {{z^2} - 1}}} $$ is ________________.
The value of the integral $${1 \over {\pi j}}\oint\limits_C {{{dz} \over {{z^2} - 1}}} $$ is ________________.
 The value of the integral $${1 \over {\pi j}}\oint\limits_C {{{dz} \over {{z^2} - 1}}} $$ is ________________.
The value of the integral $${1 \over {\pi j}}\oint\limits_C {{{dz} \over {{z^2} - 1}}} $$ is ________________.Your input ____
2
GATE ECE 2017 Set 2
MCQ (Single Correct Answer)
+2
-0.6
An integral $${\rm I}$$ over a counter clock wise circle $$C$$ is given by $${\rm I} = \oint\limits_c {{{{z^2} - 1} \over {{z^2} + 1}}} \,\,{e^z}\,dz$$
If $$C$$ is defined as $$\left| z \right| = 3,$$ then the value of $${\rm I}$$ is
If $$C$$ is defined as $$\left| z \right| = 3,$$ then the value of $${\rm I}$$ is
3
GATE ECE 2016 Set 2
Numerical
+2
-0
Consider the complex valued function $$f\left( z \right) = 2{z^3} + b{\left| z \right|^3}$$ where $$z$$ is a complex variable. The value of $$b$$ for which the function $$f(z)$$ is analytic is __________.
Your input ____
4
GATE ECE 2016 Set 1
Numerical
+2
-0
In the following integral, the contour $$C$$ encloses the points $${2\pi j}$$ and $$-{2\pi j}$$. The value of the integral $$ - {1 \over {2\pi }}\oint\limits_c {{{\sin z} \over {{{\left( {z - 2\pi j} \right)}^3}}}} dz$$ is ___________.
Your input ____
Questions Asked from Marks 2
GATE ECE Subjects
Signals and Systems
Network Theory
Control Systems
Digital Circuits
General Aptitude
Electronic Devices and VLSI
Analog Circuits
Engineering Mathematics
Microprocessors
Communications
Electromagnetics