ExamSIDE
Questions (Powered by ExamGOAL)
Engineering Mathematics
Linear Algebra
Marks 1Marks 2
Calculus
Marks 1Marks 2
Vector Calculus
Marks 1Marks 2
Complex Variable
Marks 1Marks 2
Probability and Statistics
Marks 1Marks 2
Differential Equations
Marks 1Marks 2
Numerical Methods
Marks 1Marks 2
Transform Theory
Marks 1Marks 2
Next
1
GATE ECE 2025
MCQ (More than One Correct Answer)
+2
-0

Which of the following statements involving contour integrals (evaluated counter-clockwise) on the unit circle $C$ in the complex plane is/are TRUE?

A
$\oint_C e^z d z=0$
B
$\oint_C z^n d z=0$, where $n$ is an even integer
C
$\oint_C \cos z d z \neq 0$
D
$\oint_C \sec z d z \neq 0$
2
GATE ECE 2024
MCQ (Single Correct Answer)
+2
-1.33

Let $z$ be a complex variable. If $f(z)=\frac{\sin(\pi z)}{z^{7}(z-2)}$ and $C$ is the circle in the complex plane with $|z|=3$ then $\oint\limits_{C} f(z)dz$ is _______.

A

$ \pi^2 j $

B

$ j\pi\left(\frac{1}{2}-\pi\right) $

C

$ j\pi\left(\frac{1}{2}+\pi\right) $

D

$-\pi^2 j$

3
GATE ECE 2022
MCQ (More than One Correct Answer)
+2
-0

Consider the following series :

$$\sum\limits_{n = 1}^\infty {{{{n^d}} \over {{c^n}}}} $$

For which of the following combinations of c, d values does this series converge?

A
c = 1, d = $$-$$1
B
c = 2, d = 1
C
c = 0.5, d = $$-$$10
D
c = 1, d = $$-$$2
4
GATE ECE 2018
Numerical
+2
-0
The contour C given below is on the complex plane $$z = x + jy$$, where $$j = \sqrt { - 1} $$. 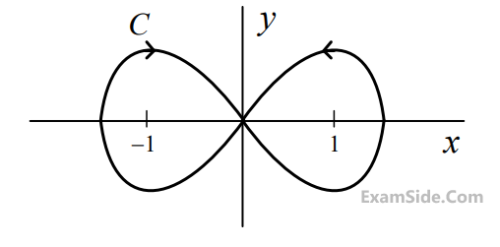GATE ECE 2018 Engineering Mathematics - Complex Variable Question 6 English The value of the integral $${1 \over {\pi j}}\oint\limits_C {{{dz} \over {{z^2} - 1}}} $$ is ________________.
Your input ____
Next
Questions Asked from Marks 2
GATE ECE 2025 (1) GATE ECE 2024 (1) GATE ECE 2022 (1) GATE ECE 2018 (1) GATE ECE 2017 Set 2 (1) GATE ECE 2016 Set 2 (1) GATE ECE 2016 Set 1 (1) GATE ECE 2016 Set 3 (1) GATE ECE 2015 Set 2 (2) GATE ECE 2015 Set 1 (1) GATE ECE 2015 Set 3 (1) GATE ECE 2012 (2) GATE ECE 2007 (1)
GATE ECE Subjects
Signals and Systems
Network Theory
Control Systems
Digital Circuits
General Aptitude
Electronic Devices and VLSI
Analog Circuits
Engineering Mathematics
Microprocessors
Communications
Electromagnetics