Signals and Systems
Miscellaneous
Marks 21
GATE EE 2022
MCQ (Single Correct Answer)
+2
-0.67
Let an input x(t) = 2 sin(10$$\pi$$t) + 5 cos(15$$\pi$$t) + 7 sin(42$$\pi$$t) + 4 cos(45$$\pi$$t) is passed through an LTI system having an impulse response,
$$h(t) = 2\left( {{{\sin (10\pi t)} \over {\pi t}}} \right)\cos (40\pi t)$$
The output of the system is
2
GATE EE 2016 Set 1
MCQ (Single Correct Answer)
+2
-0.6
Suppose x1(t) and x2(t) have the Fourier transforms as shown below.
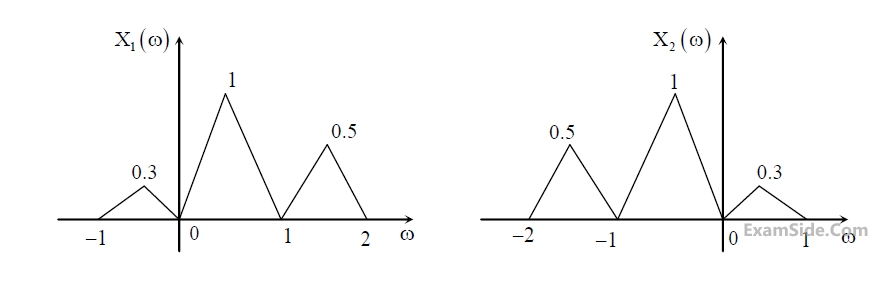 Which one of the following statements is TRUE?
Which one of the following statements is TRUE?
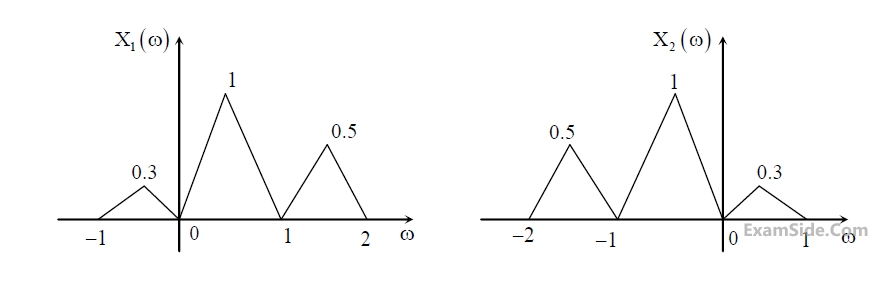 Which one of the following statements is TRUE?
Which one of the following statements is TRUE?3
GATE EE 2015 Set 2
MCQ (Single Correct Answer)
+2
-0.6
Consider a signal defined by $$$x\left(t\right)=\left\{\begin{array}{l}e^{j10t}\;\;\;for\;\left|t\right|\leq1\\0\;\;\;\;\;\;\;for\;\;\left|t\right|>1\end{array}\right.$$$
Its Fourier Transform is
4
GATE EE 2014 Set 2
MCQ (Single Correct Answer)
+2
-0.6
A 10 kHz even-symmetric square wave is passed through a bandpass filter with centre
frequency at 30 kHz and 3 dB passband of 6 kHz. The filter output is
GATE EE Subjects
Electromagnetic Fields
Signals and Systems
Engineering Mathematics
General Aptitude
Power Electronics
Power System Analysis
Analog Electronics
Control Systems
Digital Electronics
Electrical Machines
Electric Circuits
Electrical and Electronics Measurement