Let $${H_1}(z) = {(1 - p{z^{ - 1}})^{ - 1}},{H_2}(z) = {(1 - q{z^{^{ - 1}}})^{ - 1}}$$ , H(z) =$${H_1}(z)$$ +r $${H_2}$$. The quantities p, q, r are real numbers. Consider , p=$${1 \over 2}$$, q=-$${1 \over 4}$$ $$\left| r \right|$$ <1. If the zero H(z) lies on the unit circle, the r = ____________________________.

The input-output relationship of a causal stable LTI system is given as
𝑦[𝑛] = 𝛼 𝑦[𝑛 − 1] + $$\beta $$ x[n].
If the impulse response h[n] of this system satisfies the condition $$\sum\limits_{n = 0}^\infty h $$[n] = 2, the relationship between α and is $$\alpha $$ and $$\beta $$ is

Let x $$\left[ n\right]$$= $${\left( { - {1 \over 9}} \right)^n}\,u(n) - {\left( { - {1 \over 3}} \right)^n}u( - n - 1).$$ The region of Convergence (ROC) of the z-tansform of x$$\left[ n \right]$$

In the following network (Fig.1), the switch is closed at t = 0 and the sampling starts from t=0. The sampling frequency is 10 Hz.

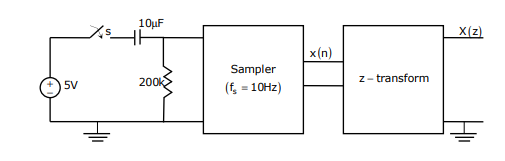
The samples x (n) (n=0, 1, 2,...........) are given by