Signals and Systems
Miscellaneous
Marks 21
GATE EE 2014 Set 1
MCQ (Single Correct Answer)
+2
-0.6
Let f(t) be a continuous time signal and let F($$\omega$$) be its Fourier Transform defined by $$F\left(\omega\right)=\int_{-\infty}^\infty f\left(t\right)e^{-j\omega t}dt$$. Define g(t) by $$g\left(t\right)=\int_{-\infty}^\infty F\left(u\right)e^{-jut}du$$. What is the relationship between f(t) and g(t)?
2
GATE EE 2012
MCQ (Single Correct Answer)
+2
-0.6
The Fourier transform of a signal h(t) is $$H\left(j\omega\right)=\left(2\cos\omega\right)\left(\sin2\omega\right)/\omega$$. The value of h(0) is
3
GATE EE 2010
MCQ (Single Correct Answer)
+2
-0.6
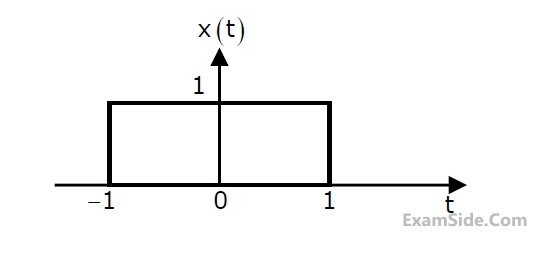
x(t) is a positive rectangular pulse from t = -1 to t = +1 with unit height as shown
in the figure. The value of $$\int_{-\infty}^\infty\left|X\left(\omega\right)\right|^2d\omega$$ {where X($$\mathrm\omega$$) is the Fourier transform of
x(t)} is

GATE EE Subjects
Electromagnetic Fields
Signals and Systems
Engineering Mathematics
General Aptitude
Power Electronics
Power System Analysis
Analog Electronics
Control Systems
Digital Electronics
Electrical Machines
Electric Circuits
Electrical and Electronics Measurement