Control Systems
1
GATE EE 2015 Set 1
MCQ (Single Correct Answer)
+2
-0.6
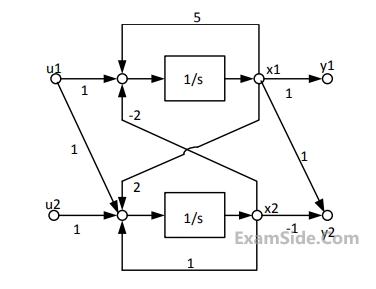
In the signal flow diagram given in the figure, $${u_1}$$ and $${u_2}$$ are possible inputs whereas $${y_1}$$ and $${y_2}$$ are possible outputs. When would the $$SISO$$ system derived from this diagram be controllable and observable?

2
GATE EE 2015 Set 2
MCQ (Single Correct Answer)
+2
-0.6
For the system governed by the set of equations:
$$$\eqalign{
& d{x_1}/dt = 2{x_1} + {x_2} + u \cr
& d{x_2}/dt = - 2{x_1} + u \cr
& \,\,\,\,\,\,y = 3{x_1} \cr} $$$
the transfer function $$Y(s)/U(s)$$ is given by
the transfer function $$Y(s)/U(s)$$ is given by
3
GATE EE 2014 Set 2
MCQ (Single Correct Answer)
+2
-0.6
The second order dynamic system $${{dX} \over {dt}} = PX + Qu,\,\,\,y = RX$$ has the matrices $$P,Q,$$ and $$R$$ as follows: $$P = \left[ {\matrix{
{ - 1} & 1 \cr
0 & { - 3} \cr
} } \right]\,\,Q = \left[ {\matrix{
0 \cr
1 \cr
} } \right]$$
$$R = \left[ {\matrix{ 0 & 1 \cr } } \right]$$ The system has the following controllability and observability properties:
$$R = \left[ {\matrix{ 0 & 1 \cr } } \right]$$ The system has the following controllability and observability properties:
4
GATE EE 2014 Set 3
MCQ (Single Correct Answer)
+2
-0.6
Consider the system described by the following state space equations
$$$\eqalign{
& \left[ {\matrix{
{{x_1}} \cr
{{x_2}} \cr
} } \right] = \left[ {\matrix{
0 & 1 \cr
{ - 1} & { - 1} \cr
} } \right]\left[ {\matrix{
{{x_1}} \cr
{{x_2}} \cr
} } \right] + \left[ {\matrix{
0 \cr
1 \cr
} } \right]u; \cr
& y = \left[ {\matrix{
1 & 0 \cr
} } \right]\left[ {\matrix{
{{x_1}} \cr
{{x_2}} \cr
} } \right] \cr} $$$
If $$u$$ unit step input, then the steady state error of the system is
Questions Asked from Marks 2
GATE EE 2025 (1) GATE EE 2023 (1) GATE EE 2017 Set 2 (1) GATE EE 2017 Set 1 (1) GATE EE 2016 Set 1 (1) GATE EE 2015 Set 1 (1) GATE EE 2015 Set 2 (1) GATE EE 2014 Set 2 (1) GATE EE 2014 Set 3 (1) GATE EE 2013 (2) GATE EE 2012 (1) GATE EE 2010 (1) GATE EE 2009 (2) GATE EE 2008 (2) GATE EE 2005 (2) GATE EE 2004 (1) GATE EE 2003 (1) GATE EE 2002 (2)
GATE EE Subjects
Electromagnetic Fields
Signals and Systems
Engineering Mathematics
General Aptitude
Power Electronics
Power System Analysis
Analog Electronics
Control Systems
Digital Electronics
Electrical Machines
Electric Circuits
Electrical and Electronics Measurement