Signals and Systems
1
GATE ECE 2008
MCQ (Single Correct Answer)
+2
-0.6
In the following network (Fig .1), the switch is closed at t = 0- and the sampling starts from t = 0. The sampling frequency is 10 Hz.
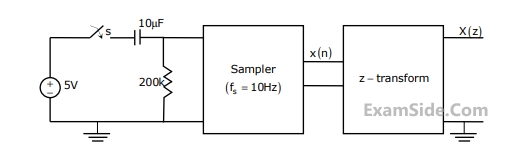
The expression and the region of convergence of the z-transform of the sampled signal are

The expression and the region of convergence of the z-transform of the sampled signal are
2
GATE ECE 2007
MCQ (Single Correct Answer)
+2
-0.6
The z-transform X (z) f a sequence x$$\left[ n \right]$$ is given by = $${{0.5} \over {1 - 2{z^{ - 1}}}}$$ . It is given that the region of convergence of X$$\left[ z \right]$$ includes the unit circle. The value of x$$\left[ 0 \right]$$ is
3
GATE ECE 1999
MCQ (Single Correct Answer)
+2
-0.6
The z-transform of a signal is given by c(z)=$${1 \over 4}{{{z^{ - 1}}(1 - {z^{ - 4}})} \over {{{(1 - {z^{ - 1}})}^2}}}$$. Its final value is
4
GATE ECE 1990
MCQ (Single Correct Answer)
+2
-0.6
The Z-transform of the following real exponential sequence:
x(nT) = $${a^n}$$, nT $$ \ge $$ 0
=0, nT<0, a> 0
gives us by
x(nT) = $${a^n}$$, nT $$ \ge $$ 0
=0, nT<0, a> 0
gives us by
GATE ECE Subjects
Signals and Systems
Network Theory
Control Systems
Digital Circuits
General Aptitude
Electronic Devices and VLSI
Analog Circuits
Engineering Mathematics
Microprocessors
Communications
Electromagnetics