In a connected graph, bridge is an edge whose removal disconnects a graph. Which one of the following statements is true?

Suppose L = { p, q, r, s, t } is a lattice represented by the following Hasse diagram: 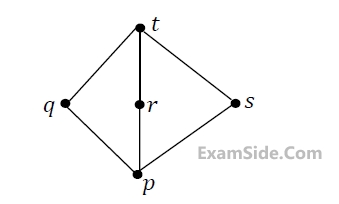For any $$x, y ∈ L$$, not necessarily distinct, $$x ∨ y$$ and x ∧ y are join and meet of x, y, respectively. Let $$L^3 = \left\{\left(x, y, z\right): x, y, z ∈ L\right\}$$ be the set of all ordered triplets of the elements of L. Let p_r be the probability that an element $$\left(x, y,z\right) ∈ L^3$$ chosen equiprobably satisfies $$x ∨ (y ∧ z) = (x ∨ y) ∧ (x ∨ z)$$. Then

Let G be a connected planar graph with 10 vertices. If the number of edges on each face is three, then the number of edges in G is ___________.

If $$G$$ is a forest with $$n$$ vertices and $$k$$ connected components, how many edges does $$G$$ have?