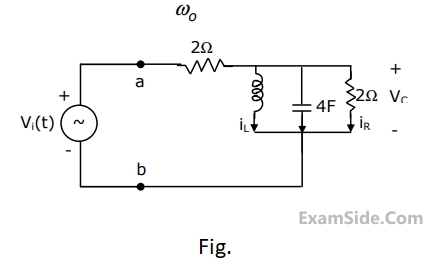
(a)Find the frequency $${\omega _0}$$ at which the magnitude of the impedance across terminals a, b reaches maximum.
(b) Find the impedance across a, b at the frequency $${\omega _0}$$.
(c) If $${v_i}\left( t \right) = V\,\,\sin \left( {{\omega _0}t} \right),$$ find $${i_L}\left( t \right),\,\,{i_c}\left( t \right),{i_R}\left( t \right).$$
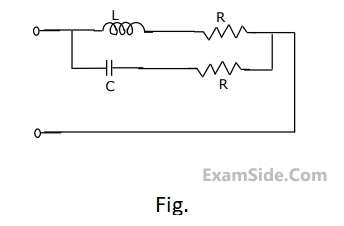

(a) Find the impedance to the right of $$\left( {A,\,\,\,\,\,\,B} \right)$$ at $$\omega \,\,\, = \,\,\,\,0$$ rad/sec and $$\omega \,\,\, = \,\,\,\,\infty $$ rad/sec.
(b) If $$\omega \,\,\, = \,\,\,\,{\omega _0}$$ rad/sec and $${i_1}\left( t \right) = \,\,{\rm I}\,\,\,\sin \,\left( {{\omega _0}t} \right)\,{\rm A},$$ where $${\rm I}$$ is positive, $${{\omega _0}\,\, \ne \,\,0}$$, $${{\omega _0}\,\, \ne \,\,\infty }$$, then find $${\rm I}$$, $${{\omega _0}}$$ and $${i_2}\left( t \right)$$