Signals and Systems
1
GATE ECE 2005
MCQ (Single Correct Answer)
+2
-0.6
For a signal x(t) the Fourier transform is X(f). Then the inverse Fourier transform of X(3f+2) is given by
2
GATE ECE 2004
MCQ (Single Correct Answer)
+2
-0.6
Let x(t) and y(t) (with Fourier transforms X(f) and Y(f) respectively) be related as shown in Fig.(1) & (2).
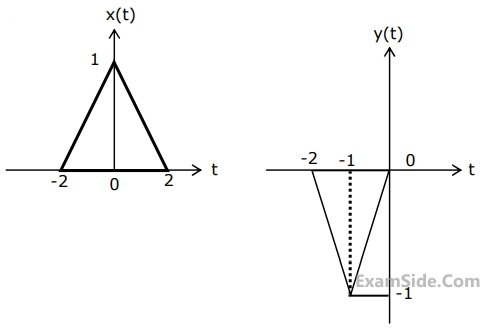

Then Y(f) is
3
GATE ECE 2000
MCQ (Single Correct Answer)
+2
-0.6
The Hilbert transform of $$\left[ {\cos \,{\omega _1}t + \,\sin {\omega _2}t\,} \right]$$ is
4
GATE ECE 1997
MCQ (Single Correct Answer)
+2
-0.6
If the Fourier Transfrom of a deterministic signal g(t) is G (f), then
Match each of the items 1, 2 on the left with the most appropriate item A, B, C or D on the right.
Item-1
(1) The Fourier transform of g (t - 2) is
(2) The Fourier transform of g (t/2) is
Item - 2
(A) G(f) $$e^{-j\left(4\mathrm{πf}\right)}$$
(B) G(2f)
(C) 2G(2f)
(D) G(f-2)
Match each of the items 1, 2 on the left with the most appropriate item A, B, C or D on the right.
GATE ECE Subjects
Signals and Systems
Network Theory
Control Systems
Digital Circuits
General Aptitude
Electronic Devices and VLSI
Analog Circuits
Engineering Mathematics
Microprocessors
Communications
Electromagnetics