For a power system the admittance and impedance matrices for the fault studies are as follows. $$$\eqalign{ & {Y_{bus}} = \left[ {\matrix{ { - j8.75} & {j1.25} & {j2.50} \cr {j1.25} & { - j6.25} & {j2.50} \cr {j2.50} & {j2.50} & { - j5.00} \cr } } \right] \cr & {Z_{bus}} = \left[ {\matrix{ {j0.16} & {j0.08} & {j0.12} \cr {j0.08} & {j0.24} & {j0.16} \cr {j0.12} & {j0.16} & {j0.34} \cr } } \right] \cr} $$$

The pre-fault voltages are $$1.0$$ $$p.u.$$ at all the buses. The system was unloaded prior to the fault. A solid $$3$$ phase fault takes place at bus $$2.$$

The post fault voltages at buses $$1$$ and $$3$$ in per unit respectively are

For a power system the admittance and impedance matrices for the fault studies are as follows. $$$\eqalign{ & {Y_{bus}} = \left[ {\matrix{ { - j8.75} & {j1.25} & {j2.50} \cr {j1.25} & { - j6.25} & {j2.50} \cr {j2.50} & {j2.50} & { - j5.00} \cr } } \right] \cr & {Z_{bus}} = \left[ {\matrix{ {j0.16} & {j0.08} & {j0.12} \cr {j0.08} & {j0.24} & {j0.16} \cr {j0.12} & {j0.16} & {j0.34} \cr } } \right] \cr} $$$

The pre-fault voltages are $$1.0$$ $$p.u.$$ at all the buses. The system was unloaded prior to the fault. A solid $$3$$ phase fault takes place at bus $$2.$$

The per unit fault feeds from generators connected to buses $$1$$ and $$2$$ respectively are

The Gauss Seidel load flow method has following disadvantages. Tick the incorrect student.

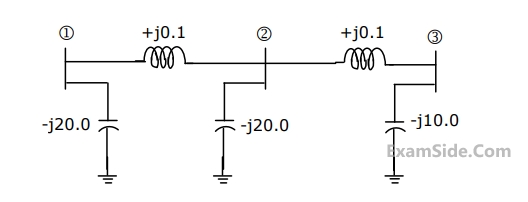
The network shown in the given figure has impedances in p.u. as indicated. The diagonal element $$Y22$$ of the bus admittance matrix $${Y_{BUS}}$$ of the network is