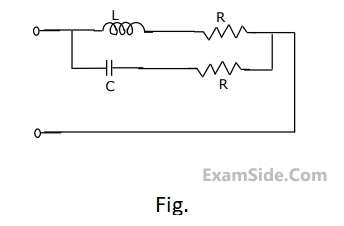
Determine the frequency of resonance and the resonant impedance of the parallel circuit shown in figure. What happens when $$L = C{R^2}$$?

In the circuit of Fig., all currents and voltage are sinusoids of frequency $$\omega $$ rad/sec.

(a) Find the impedance to the right of $$\left( {A,\,\,\,\,\,\,B} \right)$$ at $$\omega \,\,\, = \,\,\,\,0$$ rad/sec and $$\omega \,\,\, = \,\,\,\,\infty $$ rad/sec.

(b) If $$\omega \,\,\, = \,\,\,\,{\omega _0}$$ rad/sec and $${i_1}\left( t \right) = \,\,{\rm I}\,\,\,\sin \,\left( {{\omega _0}t} \right)\,{\rm A},$$ where $${\rm I}$$ is positive, $${{\omega _0}\,\, \ne \,\,0}$$, $${{\omega _0}\,\, \ne \,\,\infty }$$, then find $${\rm I}$$, $${{\omega _0}}$$ and $${i_2}\left( t \right)$$

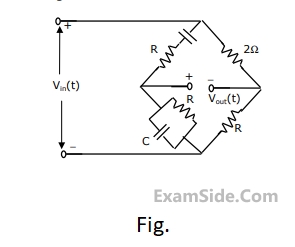
Calculate the frequency at which zero- transmission is obtained from the Wien- bridge shown in Fig.

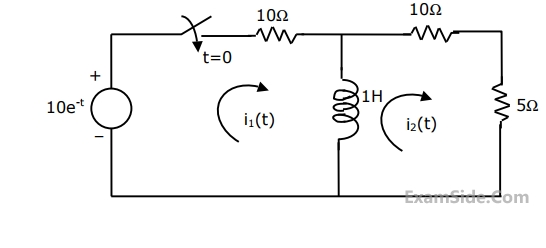
Write down the mesh equation of the following network in terms of i₁(t) and i₂(t).Derive the differential equation for i₁(t) from these and solve it.