ExamSIDE
Questions (Powered by ExamGOAL)
Control Systems
Signal Flow Graph and Block Diagram
Marks 1Marks 2Marks 5
Time Response Analysis
Marks 1Marks 2Marks 5Marks 8Marks 10
Compensators
Marks 1Marks 2Marks 5Marks 8
Basic of Control Systems
Marks 1Marks 2
Frequency Response Analysis
Marks 1Marks 2Marks 5Marks 8Marks 10
Stability
Marks 1Marks 2Marks 5
Root Locus Diagram
Marks 1Marks 2
State Space Analysis
Marks 1Marks 2Marks 5Marks 10
Previous Next
1
GATE ECE 2014 Set 2
MCQ (Single Correct Answer)
+2
-0.6
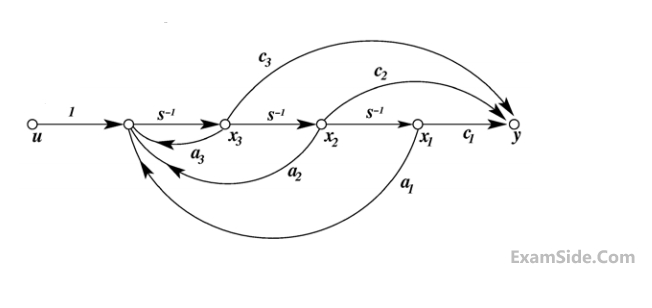
Consider the state space system expressed by the signal flow diagram shown in the figure. GATE ECE 2014 Set 2 Control Systems - State Space Analysis Question 18 English

The corresponding system is

A
always controllable
B
always observable
C
always stable
D
always unstable
2
GATE ECE 2014 Set 2
MCQ (Single Correct Answer)
+2
-0.6
An unforced linear time invariant (LTI) system is represented by $$$\left[ {\matrix{ {\mathop {{x_1}}\limits^ \bullet } \cr {\mathop {{x_2}}\limits^ \bullet } \cr } } \right] = \left[ {\matrix{ { - 1} & 0 \cr 0 & { - 2} \cr } } \right]\left[ {\matrix{ {{x_1}} \cr {{x_2}} \cr } } \right].$$$

If the initial conditions are x1(0)= 1 and x2(0)=-1, the solution of the state equation is

A
$${x_1}\left( t \right) = - 1,{x_2}\left( t \right) = 2$$
B
$${x_1}\left( t \right) = - {e^{ - t}},{x_2}\left( t \right) = 2{e^{ - t}}$$
C
$${x_1}\left( t \right) = {e^{ - t}},{x_2}\left( t \right) = - {e^{ - 2t}}$$
D
$${x_1}\left( t \right) = {e^{ - t}},{x_2}\left( t \right) = - 2{e^{ - t}}$$
3
GATE ECE 2014 Set 1
MCQ (Single Correct Answer)
+2
-0.6
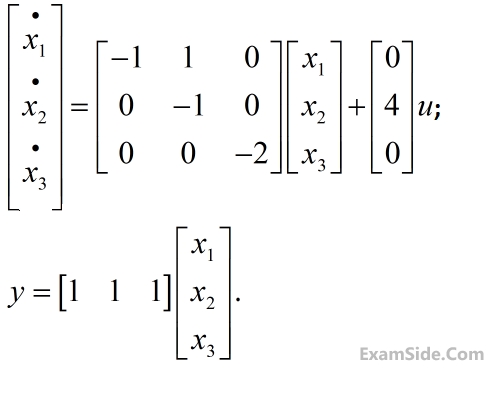
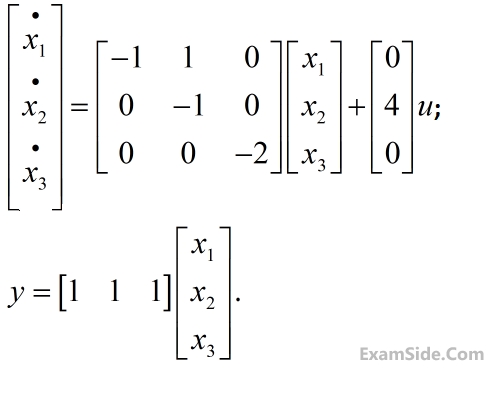
Consider the state space model of a system, as given below GATE ECE 2014 Set 1 Control Systems - State Space Analysis Question 20 English

The system is

A
controllable and observable.
B
uncontrollable and observable.
C
uncontrollable and unobservable.
D
controllable and unobservable.
4
GATE ECE 2013
MCQ (Single Correct Answer)
+2
-0.6
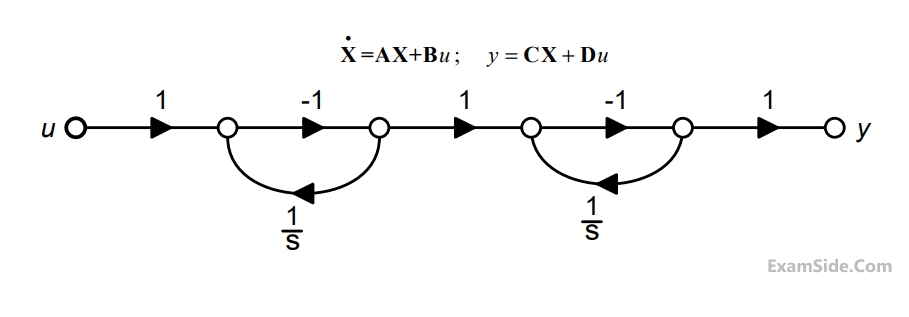
The state diagram of a system is shown below. A system is shown below. A system is described by the state variable equations GATE ECE 2013 Control Systems - State Space Analysis Question 21 English

The state transition matrix eAt of the system shown in the figure above is

A
$$\left[ {\matrix{ {{e^{ - t}}} & 0 \cr {t{e^{ - t}}} & {{e^{ - t}}} \cr } } \right]$$ v
B
$$\left[ {\matrix{ {{e^{ - t}}} & 0 \cr { - t{e^{ - t}}} & {{e^{ - t}}} \cr } } \right]$$
C
$$\left[ {\matrix{ {{e^{ - t}}} & 0 \cr {{e^{ - t}}} & {{e^{ - t}}} \cr } } \right]$$
D
$$\left[ {\matrix{ {{e^{ - t}}} & { - t{e^{ - t}}} \cr 0 & {{e^{ - t}}} \cr } } \right]$$
Previous Next
Questions Asked from Marks 2
GATE ECE 2025 (1) GATE ECE 2024 (1) GATE ECE 2018 (1) GATE ECE 2017 Set 2 (1) GATE ECE 2016 Set 3 (1) GATE ECE 2015 Set 2 (1) GATE ECE 2015 Set 3 (1) GATE ECE 2014 Set 4 (1) GATE ECE 2014 Set 3 (1) GATE ECE 2014 Set 2 (2) GATE ECE 2014 Set 1 (1) GATE ECE 2013 (2) GATE ECE 2012 (1) GATE ECE 2011 (1) GATE ECE 2010 (2) GATE ECE 2008 (1) GATE ECE 2007 (3) GATE ECE 2006 (1) GATE ECE 2004 (3) GATE ECE 2003 (1) GATE ECE 1999 (1) GATE ECE 1997 (1) GATE ECE 1992 (1) GATE ECE 1991 (1)
GATE ECE Subjects
Signals and Systems
Network Theory
Control Systems
Digital Circuits
General Aptitude
Electronic Devices and VLSI
Analog Circuits
Engineering Mathematics
Microprocessors
Communications
Electromagnetics