Signals and Systems
Miscellaneous
Marks 21
GATE EE 2025
Numerical
+2
-0
An ideal low pass filter has frequency response given by
$$
H(j \omega)= \begin{cases}1, & |\omega| \leq 200 \pi \\ 0, & \text { otherwise }\end{cases}
$$
Let $h(t)$ be its time domain representation. Then $h(0)=$ ____________ (round off to the nearest integer)
Your input ____
2
GATE EE 2022
MCQ (Single Correct Answer)
+2
-0.67
Let an input x(t) = 2 sin(10$$\pi$$t) + 5 cos(15$$\pi$$t) + 7 sin(42$$\pi$$t) + 4 cos(45$$\pi$$t) is passed through an LTI system having an impulse response,
$$h(t) = 2\left( {{{\sin (10\pi t)} \over {\pi t}}} \right)\cos (40\pi t)$$
The output of the system is
3
GATE EE 2016 Set 1
MCQ (Single Correct Answer)
+2
-0.6
Suppose x1(t) and x2(t) have the Fourier transforms as shown below.
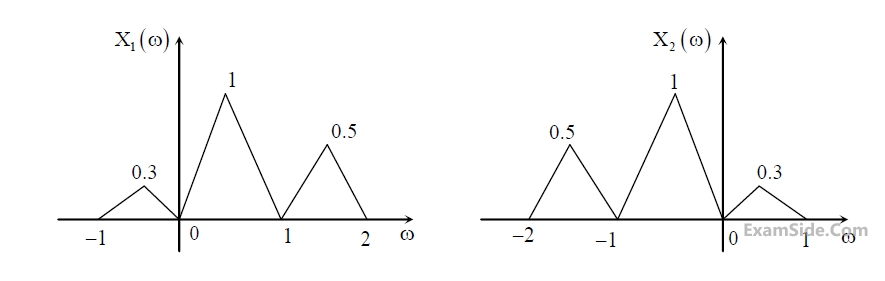 Which one of the following statements is TRUE?
Which one of the following statements is TRUE?
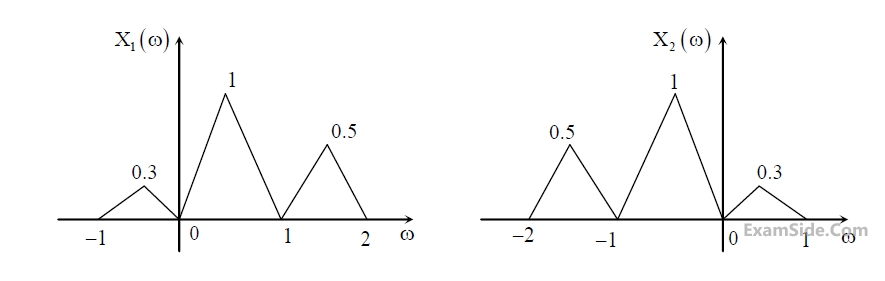 Which one of the following statements is TRUE?
Which one of the following statements is TRUE?4
GATE EE 2015 Set 2
MCQ (Single Correct Answer)
+2
-0.6
Consider a signal defined by $$$x\left(t\right)=\left\{\begin{array}{l}e^{j10t}\;\;\;for\;\left|t\right|\leq1\\0\;\;\;\;\;\;\;for\;\;\left|t\right|>1\end{array}\right.$$$
Its Fourier Transform is
GATE EE Subjects
Electromagnetic Fields
Signals and Systems
Engineering Mathematics
General Aptitude
Power Electronics
Power System Analysis
Analog Electronics
Control Systems
Digital Electronics
Electrical Machines
Electric Circuits
Electrical and Electronics Measurement