A real - values signal x(t) limited to the frequency band $$\left| f \right| \le {W \over 2}$$ is passed through a linear time invariant system whose frequency response is
$$H(f) = \left\{ {\matrix{ {{e^{ - j4\pi f}},} & {\left| f \right| \le \,{W \over 2}} \cr {0,} & {\left| f \right| > \,{W \over 2}} \cr } } \right.$$

The output of the system is

Let g(t) = $${e^{ - \pi {t^2}}}$$, and h(t) is a filter matched to g(t). If g(t) is applied as input to h(t), then the Fourier transform of the output is

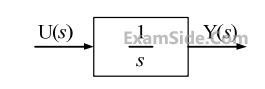
Assuming zero initial condition, the response y (t) of the system given below to a unit step input u(t) is

A system with the transfer function $${{Y(s)} \over {X(s)}} = {s \over {s + p}}\,\,$$ has an output
$$y(t) = \cos \left( {2t - {\pi \over 3}} \right)\,$$ for the input signal
$$x(t) = p\cos \left( {2t - {\pi \over 2}} \right)$$. Then, the system parameter 'p' is